Представление гармонических функций комплексными величинами.

Представим систему вращающихся векторов не в декартовой системе координат, а на комплексной плоскости, содержащей действительную (обозначена символом 1) и мнимую (символ ϳ) оси. Символ ϳ представляет собой мнимую единицу:

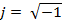(15)

Умножение любого вектора на ϳповорачивает его на угол .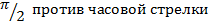

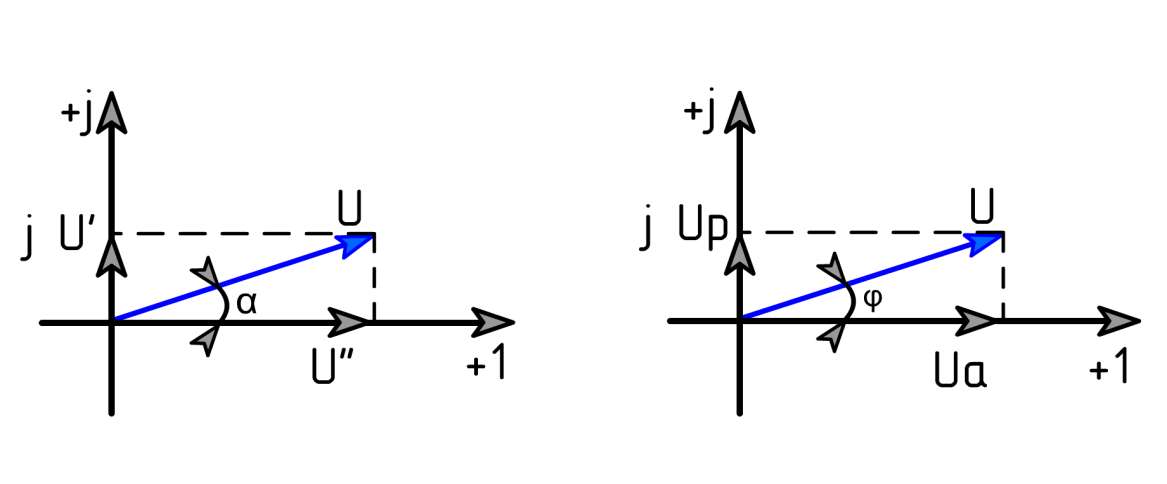
Вектор на комплексной плоскости (рис. 18а) можно представить символом, содержащим действительную и мнимую части:

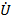= U’ + U” (16)

- алгебраическая форма записи комплексных величин.

а б

Рисунок 5.3 – изображение векторов на комплексной плоскости: символьная форма (а), физический смысл (б)

Символический метод позволяет заменить геометрические действия над векторами алгебраическими.

Помимо алгебраической формыкомплексное число можно записать в тригонометрической:

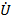= U(cosα + ϳ sinα), (17)

и показательной форме:

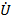= Ue^ϳα. (18)

Физический смысл действительной и мнимой частей комплексного числа можно пояснить на примере вектора напряжения (тока, сопротивления…). Действительная часть – это активная составляющая, мнимая – реактивная (рис.18б).

Исходя из этого вектор напряжения можно записать:

U = U_a + ϳU_р, (19)

где U_a – активная и U_р – реактивная составляющие напряжения.

Полное напряжение представляет собой модуль комплексного числа:

U= 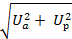. (20)

Угол αможно определить:

α = arctg 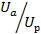. (21)

Рассмотрим выполнение операций с комплексными числами на примере сложения э.д.с. двух катушек включенных последовательносогласно (рис. 19 а).Э.д.с. первой катушки е₁ по амплитуде больше э.д.с. второй катушки е₂ и отстает от нее по фазе на угол α₌α₁ – α₂ (рис. 19 б).

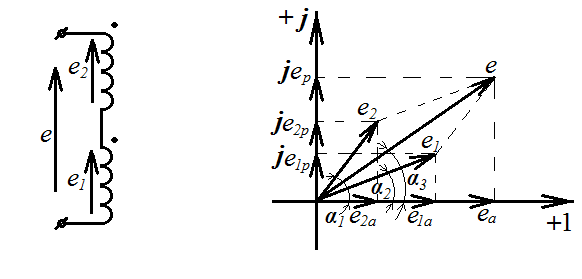
а) б)

Рисунок 5.4 – сложение э.д.с. наведенных в двух катушках: электрическая схема (а), векторная диаграмма (б)

Комплекс суммарной э.д.с.:

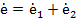. (21)

Из геометрических соотношений:

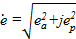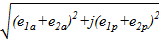= . (22)

Фазовый угол суммарной э.д.с.:

Α = arctg 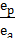. (23)