Основные логические операции цифровой электроники и правила алгебры логики

Теория построения современных логических или цифровых устройств опирается на основные логические высказывания, то есть основные положения булевой алгебры, которая полностью опирается на двоичную переменную и, основы которой, спустя почти сто лет, были реализованы в виде первых цифровых устройств.

Основные логические операции предложены английским математиком Дж. Булем в 1854 г для исследования процессов человеческих рассуждений и основаны на созданной ученым булевой алгебре. В алгебре логики используются два понятия “Да (Истина)” и “Нет (Ложь) ”.

Основные логические операции следующие:

“НЕ”(NOT)– операция инверсии (отрицания)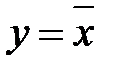

“И”(AND) – операция умножения (конъюнкции)

“ИЛИ”(OR) – операция сложения (дизъюнкции)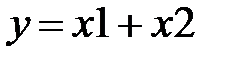

“И-НЕ”(NOT AND) – инверсия операции “И”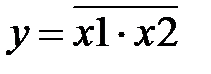

“ИЛИ-НЕ”( NOT OR ) – инверсия операции “ИЛИ”

Повторитель (Да) y = x Условные графические обозначения логических элементов и их таблицы истинности (переключений) приведены ниже.

Алгебра логики определяется следующей системой аксиом:

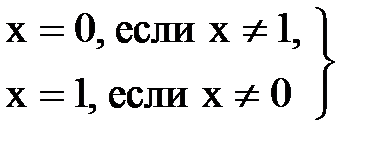(13.1)

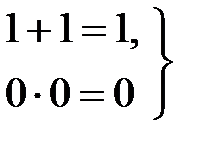(13.2)

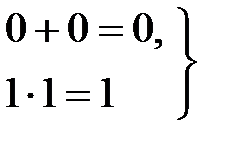(13.3)

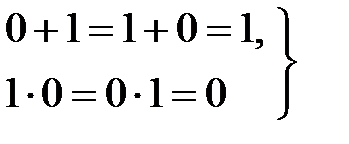(13.4)

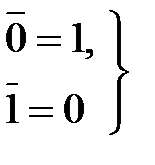(13.5)

Аксиома (13.1) утверждает, что в алгебре логики рассматриваются только двоичные переменные. Аксиомы (13.2…13.4) определяют операции дизъюнкции и конъюнкции, а аксиома (13.5) – операцию отрицания.

Если в аксиомах (13.2…13.4), заданных парами, произвести взаимную замену операций дизъюнкции и конъюнкции, а также элементов “0” и “1”, то из одной аксиомы пары можно получить другую. Это свойство называется принципом двойственности.

С помощью аксиом алгебры логики можно доказать целый ряд теорем. Одним из эффективных методов доказательства теорем является метод перебора всех значений переменных. Если теорема истинна, то с учетом аксиом (13.2…13.5) при подстановке любых значений переменных в обе части выражения, формирующего утверждение теоремы, должно получаться тождество.

В ряде случаев метод перебора не очень трудоемок ввиду того, что переменные могут принимать только два значения: “0” и “1”. Методом перебора доказываются следующие теоремы:

1) идемпотентные законы:

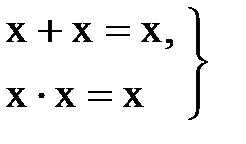(13.6)

2) коммутативные законы:

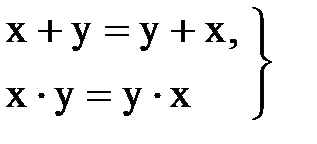(13.7)

3) ассоциативные законы:

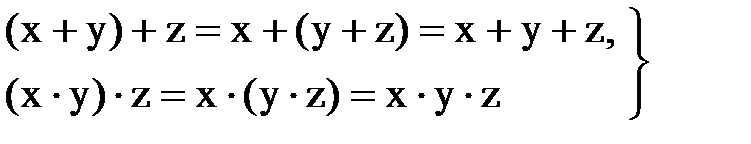(13.8)

4) дистрибутивные законы:

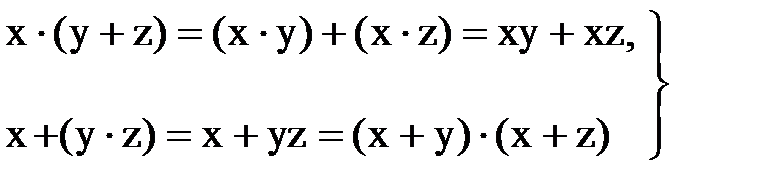(13.9)

1) законы отрицания:

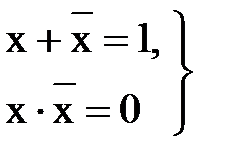(13.10

2) законы нулевого множества

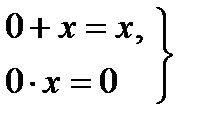(13.11) 7) законы универсального множества

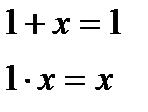(13.12)

8) законы двойственности (Теорема де Моргана):

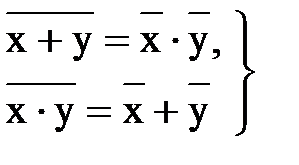(13.13)

9) закон двойного отрицания:

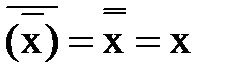. (13.14)

Теоремы (13.6 …13.13) записаны парами, причем по принципу двойственности из одной теоремы можно получить другую взаимной заменой операций дизъюнкции и конъюнкции, а также элементов “0” и “1”. Теорема (13.14) самодвойственна, так как не изменяется по принципу двойственности. Теорему (13.14) используют для формального доказательства некоторых других теорем и тождеств, не прибегая к методу перебора Вместо переменных x, y и z можно использовать логические выражения (функции), составленные из переменных с помощью операций алгебры логики. При преобразовании логических выражений должен соблюдаться определенный порядок выполнения операций (порядок старшинства): сначала отрицание, затем конъюнкция, и после этого дизъюнкция. Кроме того, в сложных логических выражениях порядок выполнения операций задается с помощью скобок.

Для упрощения логических выражений используют тождества:

1) законы поглощения

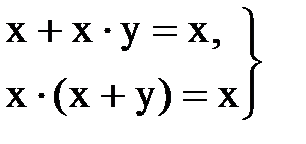(13.15)

2) операции склеивания

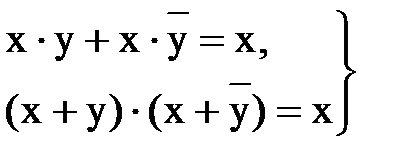(13.16)

3) операции обобщенного склеивания

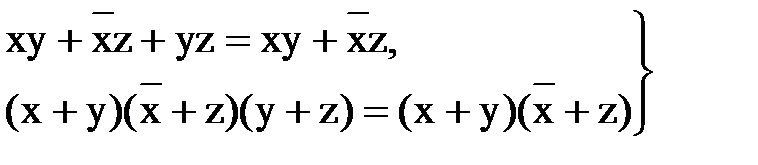(13.17)

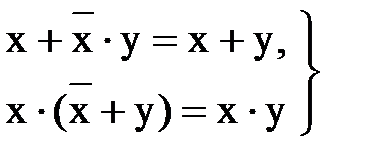(13.18)

Все тождества записаны парами на основании принципа двойственности.

Операция “штрих Шеффера” (операция И-НЕ) обозначается косой чертой и определяется соотношением:

.

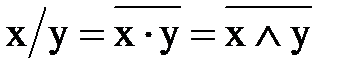Операция “стрелка Пирса” (операция ИЛИ-НЕ) обозначается символом и определяется соотношением:

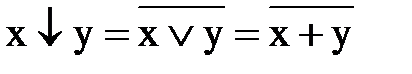. (13.19)

Операция “по модулю два” (исключающее ИЛИ, логическая неравнозначность) обозначается символом и определяется соотношением:

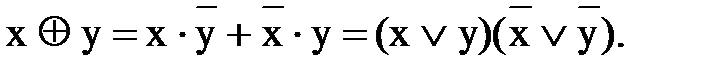
Для операции справедливы следующие тождества:

(13.20)

Отношение эквивалентности удовлетворяет следующим условиям:

а) x = x – рефлексивность

б) если x = y, то y = x – симметричность

в) если x = y, а y = z, то x = z – транзитивность.