Диапазон значений целых чисел
Рассмотрим диапазон значений целых чисел для беззнакового представления в зависимости от разрядности ячейки. Понятно, что минимальное число, которое можно записать в k битах, будет состоять из k нулей, т.е. это число 010. Максимальное число будет состоять из k единиц. Это число (k единиц в двоичной системе счисления) в десятичной системе счисления равно 2k - 1. Действительно, запишем это двоичное число в развернутой форме:
2k-1 + 2k-2 + … + 22 + 21 + 20 = 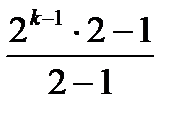 = 2k - 1
= 2k - 1
(здесь использована формула суммы конечной геометрической прогрессии). Таким образом, для беззнаковых чисел нижняя граница диапазона значений всегда равна нулю, а верхнюю границу диапазона допустимых значений можно подсчитать, зная количество разрядов, занимаемых данным числом.
При наличии одинакового числа разрядов в ячейке максимальное значение для знакового представления будет практически в два раза меньше, чем для беззнакового. Это связано с тем, что один разряд в знаковом представлении отводится под знак числа, тем самым для представления самого числа остается на один разряд меньше. Например, максимальное значение числа для знакового представления в 8-разрядной ячейке равно 127 (27 - 1), а беззнакового - 255 (28 - 1). Для 16-разрядной ячейки максимальное значение числа со знаком - 32767 (215- 1), максимальное значение чиела без знака - 65536(216 - 1), Минимальное отрицательное число, которое можно записать в 8-разрядной ячейке равно -128 (128 = 27).
Выпишем таблицу границ диапазонов для знаковых и беззнаковых представлений в ячейках с различной разрядностью.
| Разрядность | минимум (без знака) | максимум (без знака) | минимум (со знаком) | максимум (со знаком) |
| -128 | ||||
| -32768 | ||||
| -2147483648 |
При представлении чисел с фиксированной запятой все разряды ячейки, кроме знакового разряда, если он есть, служат для изображения разрядов числа. Причем каждому разряду ячейки соответствует всегда один и тот же разряд числа. Именно поэтому такое представление получило название с фиксированной запятой, так как фиксируется место запятой перед определенным разрядом (для целых чисел запятая находится после младшего разряда, т.е. вне разрядной сетки). Такая система упрощает выполнение арифметических действий, но сильно ограничивает диапазон чисел, которые можно записать в ячейку при таком представлении.
Дата добавления: 2016-12-27; просмотров: 4037;











