Волны в упругих средах.
Волна – процесс распространения колебаний в пространстве.
В волне в упругой среде (газ, жидкость, твердое тело) происходят колебания малых частиц среды. Продольные волны – частицы среды совершают колебания вдоль направления рас-пространения волны (звуковые волны). Поперечные волны – направление колебаний пер-пендикулярно напрвавлению распространения волны (волна в струне).
 Обозначим через
Обозначим через 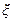 смещение частиц среды в волне относительно их положения равновесия. Тогда распределение смещений чатиц вдоль направления распространенния волны имеет вид, представленный на рис. 1. Длина волны
смещение частиц среды в волне относительно их положения равновесия. Тогда распределение смещений чатиц вдоль направления распространенния волны имеет вид, представленный на рис. 1. Длина волны 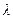 – расстояние между ближайшими точками среды, в которых колебания частиц происходят в одинаковой фазе (например, расстояние между двумя “горбами”). Скорость волны
– расстояние между ближайшими точками среды, в которых колебания частиц происходят в одинаковой фазе (например, расстояние между двумя “горбами”). Скорость волны 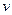 – скорость перемещения фазы колебаний частиц (скорость движения “горба”). Поэтому такую скорость называют фазовой скоростью. Из этих определений следует соотношение
– скорость перемещения фазы колебаний частиц (скорость движения “горба”). Поэтому такую скорость называют фазовой скоростью. Из этих определений следует соотношение
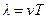 , где
, где 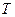 - период колебаний частиц.
- период колебаний частиц.
Уравнением волны называют зависимость
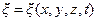 .
.
Волновая поверхность – геометрическое место точек, в которых колебания частиц в волне происходят в одинаковой фазе. В простейшем случае плоской волны волновая поверхность представляет собой плоскость.
Получим уравнение плоской волны. Пусть в плоскости 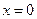 клебания частиц пароисходят по закону
клебания частиц пароисходят по закону 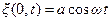 , где
, где 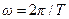 . Через время
. Через время 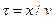 фаза колебаний в точке
фаза колебаний в точке 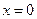 достигнет точки
достигнет точки 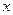 . Следовательно для смещений в точке
. Следовательно для смещений в точке 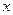 получим
получим
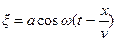 .
.
Это соотношение называется уравнением плоской волны. Для записи уравнения волны удобно ввести волновое число - 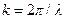 . Тогда
. Тогда 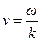 и выражение для
и выражение для 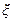 принимает вид:
принимает вид:
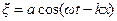 . (1)
. (1)
Такая форма уравнения обычно и используется при рассмотрении волновых процессов. Уравнение (1) описывает волну, распространяющуюся в положительном направлении оси 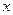 . Для волны в противоположном направлении
. Для волны в противоположном направлении
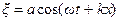 .
.
Мы будем рассматривать волны малой амплитуды. Для таких волн выполняется принцип суперпозиции
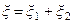 .
.
Он означает, что результатом взаимодействия двух или большего числа волн малой ампли-туды является сумма смещений частиц в каждой волне. Поэтому волны малой амплитуды называют линейными волнами. Волны большой амплитуды явлются нелинейными. Их взаимодействие происходит по более сложным законам.
Уравнение (1) соответствует случаю монохроматической волны ( 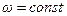 ). Этот термин сначала возник в оптике, но в дальнейшем стал использоваться и для волн в упругих средах.
). Этот термин сначала возник в оптике, но в дальнейшем стал использоваться и для волн в упругих средах.
Монохроматическая волна явлется некоторой идеализацией. На практике мы обычно имеем дело с ограниченными волновыми возмущениями (волновыми пакетами). Именно такие процессы переносят энергию и импульс в пространстве. При это пакет волн можно предста-вить в виде суммы (или группы) монохроматических волн. Он движется как целое с групповой скоростью. Для выяснения физического смысла этих понятий рассмотрим прос-тейший пример группы волн – две волны с одинаковыми амплитудами и близкими частота- ми и длинами волн:
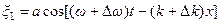 ,
, 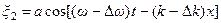 ,
,
где 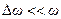 ,
, 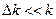 . По принципу суперпозиции суммарное смещение частиц в пакете
. По принципу суперпозиции суммарное смещение частиц в пакете
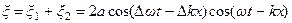 .
.
 Такой процесс называется биением волн. В этом случае основная волна модулируется по амплитуде огибающей волной с малой частотой и большой длиной волны (рис. 2). Очевидно, групповая скорость в нашем случае равна фазовой скорости огибающей волны
Такой процесс называется биением волн. В этом случае основная волна модулируется по амплитуде огибающей волной с малой частотой и большой длиной волны (рис. 2). Очевидно, групповая скорость в нашем случае равна фазовой скорости огибающей волны
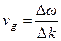 .
.
В пределе при 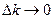 получим
получим
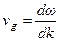 .
.
Значит, чтобы найти групповую скорость нужно знать зависимость 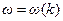 . Такая зависимость называется дисперсионным уравнением. В частности, для звука в газе
. Такая зависимость называется дисперсионным уравнением. В частности, для звука в газе 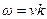 (нет дисперсии) и в этом случае
(нет дисперсии) и в этом случае 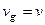 , то есть групповая скорость совпадает с фазовой. Например, для волн на поверхности воды имеет место дисперсия и
, то есть групповая скорость совпадает с фазовой. Например, для волн на поверхности воды имеет место дисперсия и 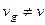 .
.
ЛЕКЦИЯ 17
Дата добавления: 2016-12-27; просмотров: 1592;











