Параметры, их величины и измерение

Термин «параметры» обозначает типы всевозможных числовых характеристик изделий, физических процессов и явлений. Он заложен в основу множества других понятий, таких как наименование параметра, обозначение параметра, наименование величины параметра, обозначение величины параметра, наименование размерности величины параметра, обозначение размерности.

Наименование параметра обычно представляется в виде одного слова, которое в тексте может быть заменено его обозначением, как правило, в виде одной его начальной буквы. Для обозначения параметров и их величин удобно применять иностранные буквы, представляющие собой сокращения иностранных наименований параметров, что позволяет достаточно быстро распознавать их в русскоязычном техническом тексте. При этом для обозначения параметров и их величин применяют одинаковые буквы, но параметры обозначают буквами обычного шрифта, а обозначения их величин — буквами курсивного начертания, например, F — частота, а F—величина частоты.

Наименование размерности величин параметров определяет Международная система единиц «СИ», в которой обозначения величин размерности, получившие названия в честь великих ученых, начинаются с большой буквы (см. табл. 3.1).

Для обозначения размерностей могут применяться сокращения их русских или иностранных наименований. Эти обозначения легко распознаются в тексте как следующие после соответствующей цифры.

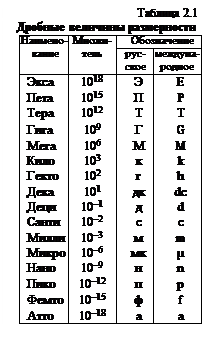
Наименования дробных величин размерности приведены в табл.2.1.

Величины параметров также выражают в децибелах (дБ), что объясняется следующим:

– число в дБ значительно меньше натурального и требует меньшие объемы памяти;

– в дБ операция умножения заменяется операцией сложения.

В общем случае дБ представляет собой логарифмическое выражение натурального безразмерного числа:

N_дБ = k·lg N,(2.1)

где: k — некоторый коэффициент;

N — натуральное десятичное безразмерное число;

N_дБ — та же величина в дБ;

lg — десятичный логарифм.

Из формулы (2.1) следует, что N_дБ будет иметь знак «минус» при N < 1.

Для выражения размерного числа в дБ необходимо предварительно размерность (р) убрать путем деления размерного числа на единицу размерности, при этом рядом со знаком «дБ» должна быть указана выбранная единица размерности («дБ/р», «дБ-р» или в другом виде), без этого обратное преобразование дБ в размерное число невозможно:

N_дБ/р = k·lg(N_р / 1_р).(2.2)

Измерение — это последовательность действий, заключающаяся в сравнении величины измеряемого параметра с эталоном, выполняемых с целью определения его величины, также называемой отсчетом. Эталоны хранятся в Главной палате мер и весов, поэтому на практике вместо них применяются средства измерений — технические средства, воспроизводящие и / или хранящие эталон величины параметра. Средства измерения также называют измерительными приборами.

В инженерной практике различают два способа измерений: прямой (непосредственный) и косвенный (опосредованный).

Прямой способ измерения предусматривает применение заранее установленного эталона измеряемой величины или его носителя (измерительного прибора) согласно методике (инструкции) его применения.

Косвенный способ измерения используют в случае невозможности или большой сложности применения прямого метода, он заключается в измерении прямым методом другой, доступной для прямого измерения, величины и последующем ее пересчете в искомую величину по заранее известной формуле.

Техническими характеристиками измерительных приборов являются режимы работы, пределы измерений, пределы входных ЭК, пределы действия органов управления и др.

Эксплуатационной характеристикой измерительного прибора является погрешность (точность, ошибка) измерений, которая в общем случае содержат случайную и систематическую составляющие. Систематическая составляющая представляет собой изученную часть случайной, поэтому известна пользователю и может быть удалена (вычтена) из общей погрешности, которая в данном случае останется чисто случайной. Среди случайных погрешностей различают: абсолютную предельную погрешность (Δ) и среднюю квадратичную погрешность (δ).

При прямых измерениях с использованием измерительного прибора величина Δ_пр равна половине цены наименьшего деления его отсчетной шкалы. При косвенных измерениях для определения величины Δ_кос достаточно применяемую в них пересчетную формулу продифференцировать и перейти от производных к конечным приращениям, в качестве которых выступают указанные величины:

Δ_кос= f (Δ_пр). (2.3)

Из теории вероятностей известно, что при достаточном количестве результатов измерений определенного параметра их погрешности подчиняются нормальному закону распределения, при котором погрешность Δ охватывает около 98 % результатов измерений и Δ ≈ 3δ. Поэтому на практике целесообразно использовать погрешность Δ,так какона почти полностью охватывает интервал возможных результатов измерений.

Формулы

Формула — это условная запись взаимосвязи величин различных параметров. В нее входят обозначения величин параметров, цифры и различные математические знаки.

В радиоэлектронике используются два вида формул, показывающих:

– взаимосвязь величин различных параметров;

– изменение величин параметров во времени (для ЭК) или в пространстве (для радиоволн).

Далее для наглядности переменные величины параметров в формулах будем отмечать знаком « _̃» (например, А̃). Примеры формул для величин параметров ЭК приведены в 3.3.

Графики

График — это отображение соответствующей формулы. В инженерной практике применяются графики с двумя осями отсчета значений аргумента и функции, изображаемыми на плоскости перпендикулярно друг другу.

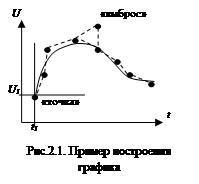График строится «по точкам», т. е. задается ряд значений аргумента (t), для которых по формуле рассчитываются соответствующие значения функции (U). Каждое значение аргумента откладывается на оси аргумента (горизонтальной), а соответствующее значение функции — на вертикальной оси, затем проводят перпендикуляры к указанным осям из засечек величин аргумента и функции и на пересечении этих перпендикуляров изображают «точку» (пример построения дан на рис.2.1). Графическое изображение функции (в общем случае это кривая) может быть получено при расчете и изображении очень большого количества «точек», которые сольются в кривую-график. На практике для исключения такой необходимости выполняют расчет разумного (по возможности побольше) количества «точек» и их превращения в «кривую» методом аппроксимации. Этот метод представляет собой подбор плавной кривой, проходящей по возможности ближе к рассчитанным «точкам». Учитывая, что ввиду возможных ошибок расчета некоторые из них могут отстоять достаточно далеко от указанной кривой, в этом случае их называют выбросами, так как при аппроксимации их выбрасывают из графика. Поэтому перед аппроксимацией следует выполнить анализ рассчитанного массива точек на наличие выбросов, для чего «точки» можно последовательно соединить отрезками прямой и определить выбросы по резкому изменению ими общей закономерности хода предполагаемого графика.

Контрольные вопросы

1. Приведите примеры кратных и дольных единиц.

2. Укажите отличие в выражении в децибелах безразмерных и размерных величин.

3. Укажите назначение измерения.

4. Дайте определение формулы и графика.