Решение обратной задачи.


2.1 Неразветвленная магнитная цепь (рис. 1.8)

Рис. 1.8
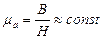Задано значение МДС w×I, требуется определить магнитный поток Ф. Если известно, что магнитная цепь устройства в рабочих режимах не насыщена и можно считать магнитную проницаемость ферромагнитных участков , то, подсчитав магнитные сопротивления участков цепи можно определить поток Ф из закона Ома для магнитной цепи: 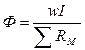. В общем же случае принимается следующий порядок решения:

2.1.1. Задаются рядом значений потока Ф (Ф’, Ф’’ и т.д.), по которым каждый раз определяется МДС wI (wI’, wI’’ и т.д. ), т.е. несколько раз решается прямая задача.

2.1.2. Строится вспомогательная магнитная характеристика Ф(wI) рис. 1.13.

2.1.3. Используя построенную характеристику, по заданному значению МДС wIзадан. определяем искомое значение потока Фиск.

Примечание: учитывая, что для расчета нужна только часть характеристики в окрестности Фиск, рекомендуется вначале найти приближенное значение Фиск с помощью уравнения 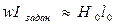(т. к. Н0 >> H1 , Н2 и Н3),

из которого определяется напряженность поля в зазоре Н0 и далее – В0 = m0S0 и приближенное значение потока Фиск=В0S0 , и далее выполняются 2.1.1 – 2.1.3 пункты расчета.

2.2. Разветвленная несимметричная магнитная цепь (рис. 1.14).

По заданному значению МДС w×I определить магнитные потоки Ф1 , Ф3 , Ф2 .

Магнитные сопротивления отдельных участков магнитопровода в общем случае нелинейные из–за нелинейной зависимости между магнитными потоками и током намагничивающей обмотки Ф(I).

Рис. 1.14
При решении задачи удобнее использовать схему замещения (рис. 1.15) магнитной цепи (рис. 1.14), подобную схеме нелинейной электрической цепи постоянного тока с той разницей, что ЭДС заменена на МДС w×I, токи в ветвях электрической цепи – потоками Ф1, Ф2 , Ф3 в ветвях магнитной цепи, нелинейные сопротивления R(I) – магнитными сопротивлениями RM(Ф).

Выделим ветвь с МДСw×I в активный двухполюсник. Второй двухполюсник, в составе которого две параллельные ветви с нелинейными магнитными сопротивлениями RM1и RM3 – пассивный (рис 1.16).

Задача решается графоаналитическим методом.

Рис. 1.15
Вебер-амперная характеристика активного двухполюсника строится в соответствии с уравнением второго закона Кирхгофа для магнитной цепи:

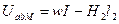1.13

Рис. 1.16
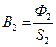Для ее построения задаемся рядом значений потока Ф2 , определяем ряд значений индукции , и по кривой намагничивания каждый раз находим напряженность магнитного поля Н2; далее по уравнению 1.13 подсчитываем соответствующие значения магнитных напряжений UabM и строим вебер-амперную характеристику активного двухполюсника Ф2(UabM)рис. 1.17.


Чтобы получить вебер-амперную характеристику пассивного двухполюсника, нужно сначала построить характеристики Ф1(UabM) и Ф3(UabM) по описанной выше методике с использованием зависимостей:

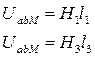
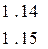
Так как ветви с потоками Ф1 , Ф3 соединены между собой параллельно и , то для построения характеристики пассивного двухполюсника Ф1(UabM)+ Ф3(UabM) складываем ординаты характеристик ветвей при одних и тех же значениях UabM.

Поскольку двухполюсники соединены последовательно (рис. 1.16), то точка пересечения их вебер – амперных характеристик определит общий для обоих магнитный поток Ф2 и магнитное напряжение UabM.

Располагая значением UabM и вебер – амперными характеристиками Ф1(UabM) и Ф3(UabM) определяем по рис. 1.17 значения потоков Ф1и Ф3.


Дата добавления: 2021-04-21; просмотров: 268;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.01 сек.