Глава 6. Преобразователи частоты.

6.1 Назначение, структурная схема, принцип работы преобразователя частоты

Преобразователь частоты (ПрЧ) служит для переноса спектра радиосигнала из одной области частот в другую без изменения характера модуляции. То есть процесс преобразования линеен относительно сигнала.

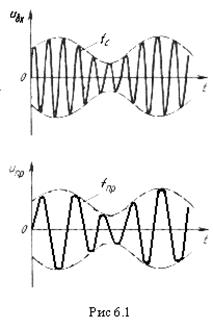
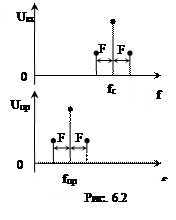На рис. 6.1 изображены эпюры напряжений сигналов на входе и выходе ПрЧ при амплитудной модуляции несущего колебания частоты f_с гармоническим сигналом частоты F. На рис. 6.2 показаны соответствующие амплитудные спектры.

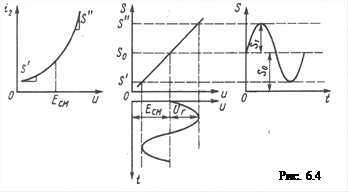
Для линейного (относительно сигнала) преобразования частоты в РПрУ используются линейные цепи с периодически меняющимся параметрами. Структурная схема ПрЧ приведена на рис. 6.3 и содержит преобразовательный элемент ПЭ, гетеродин Г и фильтр Ф.

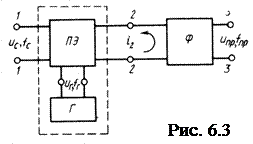ПЭ может представлять собой как активный так и пассивный элемент (транзистор, диод и т.п.) с нелинейной ВАХ, крутизна которой в разных точках различна и меняется при изменении режима работы (рис. 6.4). Назначение гетеродина – периодически с частотой f_г изменять параметры ПЭ для напряжения сигнала (прежде всего крутизну) за счёт изменения режима работы. Линейность по сигналу достигается малым уровнем входного сигнала, при котором любой участок нелинейной ВАХ для сигнала можно считать линейным (с разным значением крутизны). На рис. 6.4 приведён пример квадратичной ВАХ ПЭ. На входе ПЭ действует сумма сигнала и гетеродина, причём U_c<<U_г, а также некоторое начальное смещение Е_см. можно считать, что для сигнала под действием напряжения гетеродина периодически с частотой f_г меняется режим работы, определяемый точкой покоя на ВАХ с соответствующим значением крутизны. Например, на рис. 6.4 крутизна меняется в пределах от S' до S". На том же рисунке показаны зависимости крутизны S(U_вх) для приведенной квадратичной ВАХ (т.к. 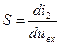, то S(U_вх) – прямая при i₂~u²_вх), и S(t) при гармоническом напряжении гетеродина.

Очевидно, что при u_г=U_гcosw_гt и линейной зависимости крутизны S(U_вх)

S(t)=S₀+ S₁ cosw_гt. (6.1)

В реальном случае помимо первой гармоники крутизны появляются высшие, характеризующие её нелинейность. Процесс преобразования удобно пояснить следующим образом.

В первом приближении, не учитывая реакции нагрузки ток на выходе ПЭ i₂(t) 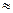S(t)u_c(t).

Пусть на входе ПЭ действует сигнал u_c(t)=U_ccos(w_ct+j_с), где U_c, j_с – функции времени, определяемые амплитудной или фазовой модуляциями. Используя зависимость (6.1) и u_c(t), для i₂(t) получим:

i₂(t) 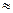(S₀+ S₁ cosw_гt) U_ccos(w_ct+j_с)=

=S₀U_ccos(w_ct+j_с)+ ½ S₁U_ccos[(w_с+w_г)t+j_с]+ ½ S₁U_ccos[(w_с-w_г)t+j_с]. (6.2)

Согласно (6.2) ток на выходе ПЭ содержит составляющие трёх частот: частоты сигнала f_c, суммарной частоты f_c+ f_г и разностной f_c- f_г (или f_г- f_с, если f_г> f_с). Очевидно, в общем случае нелинейной крутизны в выражении (6.2) добавились бы составляющие с частотами kw_г 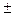w_c. Из всех составляющих полезно используется (и выделяется фильтром) только одна, чаще всего с разностной частотой:

I_2пол=1/2 S₁U_ccos[(w_с-w_г)t+j_с] (6.3)

Согласно (6.3) амплитуда полезной составляющей выходного тока (а следовательно, и выходного напряжения U_вых) пропорциональна амплитуде сигнала U_c, а фаза соответствует фазе исходного сигнала j_с, то есть при преобразовании законы модуляции, амплитуды и фазы сохраняются. Заметим, что при w_с>w_г фаза в выходном токе меняется знак, т.е. инверсна фазе входного сигнала.