Резонансного усилителя

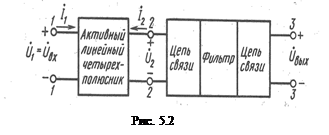Любой РУ может быть представлен в виде активного линейного четырёхполюсника, нагрузкой которого является фильтр с цепями связи (рис. 5.2).

Свойства активного четырёхполюсника описываются системой уравнений с Y – параметрами:

I₁ = Y ₁₁ U ₁ + Y ₁₂ U ₂

I ₂ = Y ₂₁U ₁ + Y ₂₂ U ₂ (5.1)

Для определения коэффициента усиления воспользуемся вторым уравнением системы (5.1).

I ₂ ‌‌‌‌‌

Здесь Y ₂₁ = — - крутизна УЭ S;

U_{1 U2 = 0}

U ₂

Y ₂₂ = ‌ ― - y_i – внутренняя проводимость УЭ

I ₁ U₁ = 0

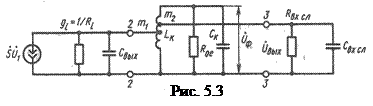Видно, что выходной ток I₂ состоит из двух составляющих I ₂ = SU ₁ + y_i U ₂ и учитывая, что y_i содержит активную и емкостную составляющие y_i=q_i + jwC_вых, эквивалентную схему выходной цепи каскада РУ (рис. 5.1) можно представить в виде рис. 5.3.

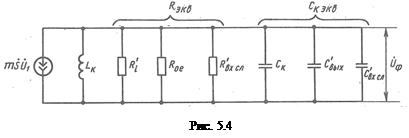
Последующий каскад, являющийся нагрузкой для данного каскада, учтён его активным входным сопротивлением и его входной емкостью. Пересчитывая элементы схемы к контуру (на основе закона сохранении энергии) в соответствии с выражениями (4.3), переходим к схеме рис. 5.4.

Получим эквивалентный колебательный контур с параметрами: С_кэкв=С_к+m₁²C_вых+m₂²C_{вх сл} (эквивалентная емкость контура с учётом внесённых ёмкостей); 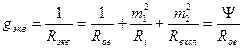- эквивалентная проводимость контура при резонансе с учётом внесённых сопротивлений; Y - коэффициент шунтирования (4.11).

По закону Ома напряжение на контуре U _ф= m₁ SU ₁ Z _экв где Z_экв – полное эквивалентное сопротивление контура. Знак минус в выражении для U_ф указывает, что ток m₁SU₁ создаёт на контуре напряжение полярности, противоположной принятой за положительную (см. рис. 5.2).

Выходное напряжение

U _вых = m₂ U _ф = - m₁ m ₂SU ₁Z _экв

и коэффициент усиления по напряжению

K = U _вых / U ₁ = - m₁ m₂ SZ_экв. (5.2)

Учитывая, что для параллельного колебательного контура Z _экв = R _экв /( 1 + jα) , где a - обобщенная расстройка, из (5.2) получим

m ₁ m₂ S R _экв

K = - ――――― (5.3)

(1 + j α )

Модуль коэффициента усиления (5.3)

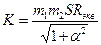. (5.4)

Резонансный коэфициент усиления из (5.4) при a=0

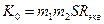. (5.5)

АЧХ усилителя

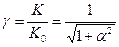(5.6)

соответствует АЧХ эквивалентного колебательного контура. Отметим, что то же выражение согласно (4.9) было получено для АЧХ одноконтурной ВЦ.

Задача оптимизации резонансного коэффициента усиления (5.5) по параметрам m₁ и m₂ решается так же как для ВУ. Максимум резонансного коэффициента усиления при заданном коэффициенте шунтирования Y (т.е. заданной полосе пропускания или g_э) реализуется при выполнении условия оптимального рассогласования, т.е. при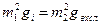

При этом

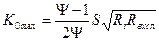. (5.7)

При высокодобротном контуре (Y>>1) теоретически достигается наибольшее значение К₀. Из (5.7) при Y>>1 имеем

.

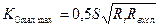Именно в этом случае реализуется одновременное согласование контура как по выходу УЭ так и по входу последующего каскада.