Глава 4. Входные цепи РПрУ

4.1. Назначения, виды и характеристики ВЦ

Входной цепью (ВЦ) называется цепь, соединяющая антенну с первым усилительным или преобразовательным каскадом приемника. Основное назначение ВЦ – передача полезного сигнала от антенны ко входу первого активного элемента (АЭ) приемника и предварительная фильтрация помех. Отсюда основные требования к показателям качества:

1. Возможно больший коэффициент передачи по мощности К_рВЦ . При этом уменьшается и коэффициент шума Ш_ВЦ=1/К_рВЦ , а следовательно, уменьшается коэффициент шума всего приемника.

2. Обеспечение предварительной фильтрации накладывает требования к селективности по зеркальному каналу Se_зк , а следовательно, и к допустимой неравномерности АЧХ в полосе пропускания приемника.

3. Обеспечение перестройки ВЦ в заданном диапазоне от f_0min до f_0max.

4. Допустимые изменения резонансного коэффициента передачи K₀ по диапазону.

5. Допустимая расстройка контуров ВЦ за счет вносимых реактивных проводимостей (в первую очередь со стороны антенны.

Обычно ВЦ представляет собой пассивный четырехполюсник, содержащий один или несколько колебательных контуров (резонаторов), настроенных на частоту принимаемого сигнала. Наибольшее распространение получили одноконтурные ВЦ, особенно в приемниках с переменной настройкой, как наиболее простые, обладающие наименьшими потерями, следовательно наибольшим К_р. В радиовещательных приемниках ДВ и СВ применяются двухконтурные ПФ.

ВЦ классифицируются по виду фильтров и способам связи входного контура с антенной и входом следующего каскада.

На рис.4.1. приведена схема с трансформаторной связью с антенной и автотрансформаторной со входом следующего каскада. В схеме рис.4.2. использованы емкостная связь с антенной и полное подключение входного контура ко входу АЭ. В схеме рис.4.3. входной контур связан с антенным фидером через автотрансформатор. Кроме того, существуют непосредственная связь входного контура с антенной (ВЦ с ферритовой магнитной антенной) и комбинированная.

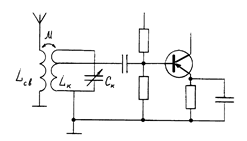
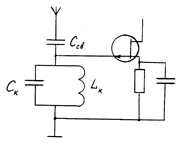
Рис.4.1 Рис.4.2

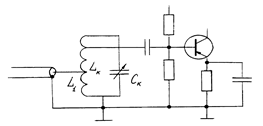
Рис.4.3

4.2. Способы настройки и перекрытия диапазона

Плавно настраивать контуры в заданном диапазоне частот можно, изменяя индуктивность или емкость (либо то и другое). Однако целесообразнее настройку осуществлять изменением емкости, так как только в этом случае добротность контура, определяющая его резонансный коэффициент передачи, не зависит от частоты настройки. Следовательно, настройка емкостью сопровождается менее резким изменением параметров контура (полоса пропускания и эквивалентное сопротивление пропорциональны частоте). При настройке емкостью коэффициент перекрытия диапазона

.

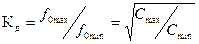Если приемник должен работать в широком диапазоне частот (К_д>3), то диапазон разбивают на поддиапазоны. Переход от одного поддиапазона на другой осуществляют переключением индуктивностей.

Основными способами разбиения диапазона на поддиапазоны являются разбиения с постоянным частотным интервалом (f_0imax-f_0imin=Df_пд=Const) и с постоянным коэффициентом перекрытия К_пд=f_0imax/f_0imin=Const. При втором способе обычно требуется меньшее число поддиапазонов, поэтому он более экономичен. В то же время с увеличением частоты в этом случае возрастает плотность настройки.

Вместо громоздких механических конденсаторов переменной емкости (КПЕ) в настоящее время обычно применяют варикапы, главное преимущество которых – малые размеры, механическая надежность, простота автоматического и дистанционного управлений настройкой. Схема включения варикапа в колебательный контур приведен на рис.4.4. Регулирующее напряжение подается потенциометром от стабилизированного источника. Резистор R нужен для уменьшения шунтирующего действия на резонансный контур цепи управления настройкой.

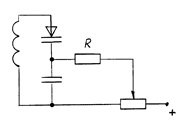
Рис.4.4

Недостатком варикапов является существенная нелинейность их характеристик. Ослабить нелинейные эффекты можно, используя встречно-последовательное включение двух варикапов.

4.3. Анализ одноконтурной входной цепи

Общие соотношения, характеризующие работу одноконтурных ВЦ, не зависят от видов связи контура, поэтому рассматривать их можно на примере любой схемы. Эквивалентная схема ВЦ с одиночным колебательным контуром приведена на рис.4.5.

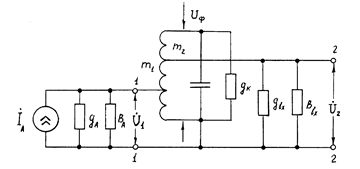
Рис.4.5

Здесь антенно-фидерная цепь представлена генератором тока I _A = E _A / Z _A с проводимостями g_A и B_A, которые включают в себя параметры элементов связи антенны с контуром R_A=R_ант+R_св; X_A= X_ант+X_св, где R_ант и X_ант - активное и реактивное сопротивление собственно антенны; R_св и X_св - активное и реактивное сопротивление элементов связи антенны с контуром. Вход первого активного элемента (АЭ) вместе с цепями смещения представлен проводимостью Y_вх=g_вх+jB_вх. Коэффициенты включения со стороны антенны и входа АЭ, соответственно определяются:

m₁ = U₁ /U _ф (4.1)

m₂ = U ₂ /U _ф (4.2)

где U_ф - напряжение на контуре.

Все элементы схемы можно пересчитать к контуру (на основе закона сохранения энергии):

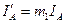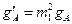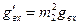; ; ; (4.3)

; ,

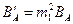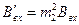где m₁ и m₂ - определяются в соответствии с (4.1), (4.2).

Тогда схема рис.4.5 преобразуется к виду рис.4.6.

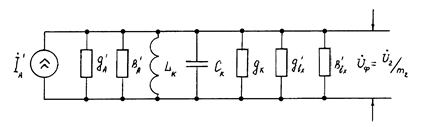
Рис.4.6

Эквивалентная реактивная составляющая проводимости контура 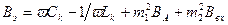, а активная составляющая g_э=g_k+m₁²g_A+m₂²g_вх. (4.4)

Теперь эквивалентная схема ВЦ может быть представлена в виде параллельного колебательного контура с эквивалентными параметрами (рис.4.7).

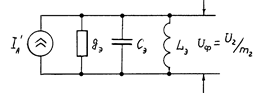
Рис.4.7

Учитывая, что U _ф = I _А /Y _ф (по закону Ома) и проведя несложные преобразования, получим выражение для комплексного коэффициента передачи ВЦ:

К_вц = U_вх /Е_А =m₁ m₂ R_э /Z_A (1 + jα) (4.5)

здесь R_{э -} эквивалентное сопротивление контура с учетом внесенных потерь;

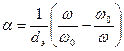- обобщенная расстройка;

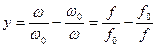- относительная расстройка.

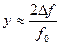Отметим, что при малых расстройках (в пределах полосы пропускания или расстройка по соседнему каналу) , где 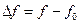- абсолютная расстройка; 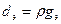- эквивалентное затухание; 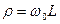- характеристическое сопротивление. Модуль коэффициента передачи (4.5)

К = m₁ m₂ R_э / |Z_А |√1 + α² (4.6)

на резонансной частоте 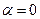и учитывая, что 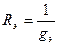в соответствии с (4.4)

m₁ m₂

K₀ = m₁ m₂ R_э /|Z_A0| = ————————————— (4.7)

|Z_A0|(g_к + m₁² g_А + m²₂ g_вх )²

где 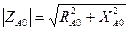- модуль полного сопротивления антенной цепи на частоте резонанса эквивалентного входного контура.

Из (4.6.) и (4.7.) получим уравнение для характеристики избирательности

K₀ |Z_A| m ₁(ω ₀) m ₂ (ω ₀)

Se = ―― = ―――――――― √1 + α² (4.8)

K(ω) | Z_A0| m ₁(ω) m ₂ (ω)

В общем случае согласно (4.8) коэффициенты m₁ и m₂ могут зависеть от частоты. Эту зависимость следует учитывать при больших расстройках 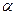(например, по зеркальному каналу).

При малых расстройках, пренебрегая изменениям Z_A и коэффициентов включения от частоты, получим

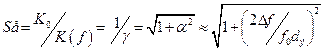, (4.9)

что совпадает с уравнением характеристики избирательности одиночного контура. Из (4.9) полоса пропускания ВЦ при заданной неравномерности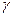

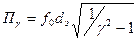, (4.10)

В частном случае при 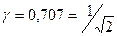из (4.10.) .

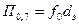4.4. Условия обеспечения максимума резонансного коэффициента передачи ВЦ

Из (4.7) видно, что значения коэффициентов включения m₁ и m₂ оказывают двоякое влияние на величину резонансного коэффициента передачи. Например, при увеличении m₁ антенна сильнее возбуждает контур, но одновременно больше шунтирует его вносимой из антенны проводимостью. Для оценки степени шунтирования контура, как со стороны антенны, так и со стороны входа АЭ, вводится коэффициент шунтирования

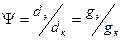. (4.11)

Тогда из (4.7.)

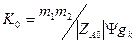. (4.12)

Чтобы определить оптимальные (с точки зрения обеспечения максимума резонансного коэффициента усиления) значения m₁ и m₂ помимо выражения для K₀ (4.12) требуется выполнение еще одного условия, накладывающего ограничение на m₁ и m₂. Очевидно, целесообразно определять оптимальные значения m₁ и m₂ при условии заданной полосы, что эквивалентно заданию d_э, g_э или .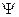

Выражая m₂ через m₁ и 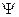, подставляя полученное выражение в (4.12), беря частную производную по m₁ и приравнивая ее нулю, получим

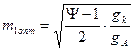. (4.13)

Аналогично

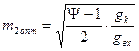. (4.14)

из (4.12.) с учетом (4.13) и (4.14)

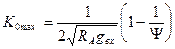. (4.15)

Из (4.13) и (4.14) видно, что коэффициент передачи K₀ ВЦ максимален при одинаковом шунтировании контура, как со стороны антенны, так и со стороны входа следующего каскада, т.е. когда

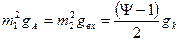. (4.16)

Очевидно, значение K_0max (4.15) зависит от коэффициента шунтирования 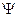. При 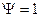(m₁=m₂=0) K_0max=0 (нет передачи энергии из антенны на вход АЭ). При 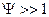(контур с малыми потерями), имеем наибольшее возможное значение .

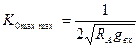В случае идеального контура без потерь равенство вносимых проводимостей (4.16) соответствует одновременному согласованию входного контура как с антенной, так и со входом следующего каскада, что и обеспечивает получение наибольшего теоретически возможного коэффициента усиления. На самом деле условие (4.16) не соответствует согласованию ни с одной стороны, поэтому иногда называется условием оптимального рассогласования.

При работе с настроенными антеннами обычно стараются согласовать цепь антенны с ВЦ. Условие согласования с антенной предполагает равенство вносимой в контур активной проводимости из антенной цепи и собственной резонансной проводимости контура с учетом внесенной входной проводимости АЭ:

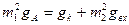. (4.17)

Из (4.17.) необходимый для согласования коэффициент включения

.

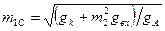Отметим, что в высокочувствительных РПрУ коэффициент шума ВЦ, определяемый совместно с УРЧ, играет существенную роль. В этом случае коэффициент включения m₁ может выбираться из соображений минимизации шума преселектора (согласование по шумам). При этом значение m₁ несколько выше, чем в режиме согласования и при малошумящем усилителе приближается к единице.

Вопросы для самопроверки

1. Какие требования предъявляются к входным цепям?

2. Как осуществляется перестройка входной цепи в диапазонных приемниках?

3. Чем определяется АЧХ входной цепи?

4. Из каких соображений могут выбираться коэффициенты включения контура (или другого фильтра) входной цепи?

5. В каком случае целесообразно использовать согласование антенны с входной цепью?

6. Какими параметрами определяется коэффициент передачи входной цепи?

7. Каковы условия получения максимального коэффициента передачи входной цепи?

8. Как осуществляется электронная перестройка контуров входной цепи? Каковы ее достоинства и недостатки?

9. Как можно классифицировать входные цепи? Приведите примеры.

10. Изобразите эквивалентную схему одноконтурной входной цепи с автотрансформаторным включением антенны и следующего каскада. Как определяются соответствующие коэффициенты включения?