Расчет параметров первой линзы

Первая линза прожектора с оптической точки зрения является иммерсионным объективом (ИО). Иммерсионная система (от лат. immersio – погружение) – оптическая система, в которой пространство между предметом и первой линзой объектива заполнено иммерсионной жидкостью (водой, раствором глицерина, минеральным маслом и др.). Применяется в микроскопах для увеличения аппертуры объектива и уменьшения отражения на поверхности его первой линзы. Задачей ИО является формирование скрещенных электронных траекторий (кроссовера), который становится объектом для второй линзы. Кроме того, в первой линзе возможно управление током луча. Полный расчет иммерсионного объектива связан со значительными трудностями, однако, введя некоторые упрощения, можно провести расчет основных характеристик ИО (Рис.3.15). Если бы электроны покидали катод без начальных скоростей, то они уходили бы по траекториям, близким к силовым линиям поля и пересекались бы в одной точке. Наличие разных начальных скоростей приводит к тому, что реальные траектории в зависимости от направления начальной скорости пересекают ось ближе или дальше точки О. При этом в плоскости, проходящей через точку О, электронные траектории лежат внутри круга с радиусом 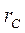. Величина 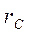является радиусом скрещения. Для определения радиуса скрещения воспользуемся теоремой Лагранжа-Гельмгольца. Поскольку в данном случае один из апертурных углов со стороны катода может изменяться от 0 до 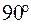, уравнение Лагранжа-Гельмгольца целесообразно переписать в виде:

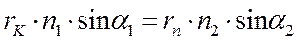(3.37)

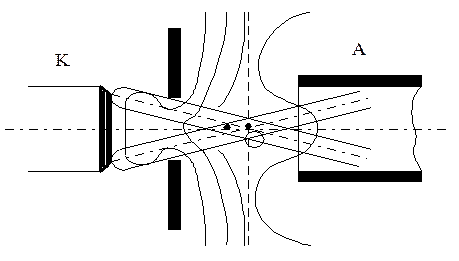
Рисунок 3.15 - Картина поля в прикатодной области ИО.

Из рисунка 3.16 видно, что

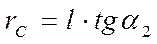(3.38)

С другой стороны

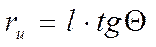(3.39)

Для параксиальных лучей можно считать, что 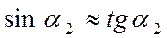, тогда

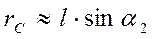(3.40)

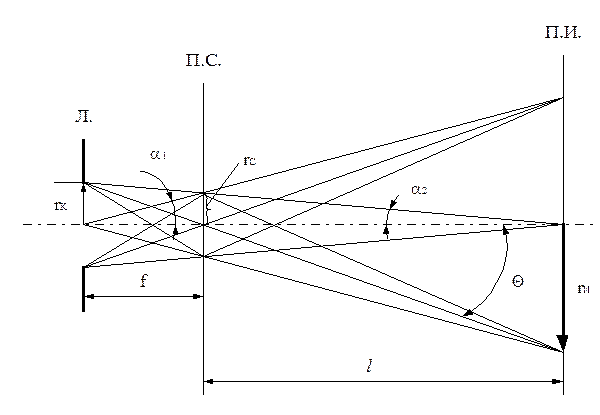
Рисунок 3.16 - Cхема формирования скрещенных электронных лучей

П.С. – плоскость скрещения;

П.И. – плоскость изображения;

Л. – линза;

F – фокусное расстояние;

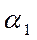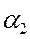, - аппертурные углы;

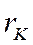- радиус катода;

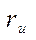- радиус изображения;

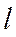- расстояние до П.И.

Подставляя последнее в (3.37), получим

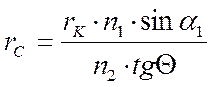, (3.41)

где ;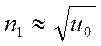

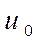- эквивалентное напряжение катода определяемое выражением:

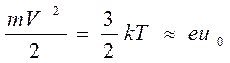, (3.42)

где 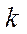- постоянная Больцмана.

Потенциал в ПС обычно близок к потенциалу ПИ, поэтому можно приблизительно считать, что, 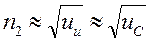, тогда

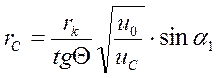(3.43)

Поскольку направление начальных скоростей равновероятно во всем интервале 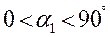, максимальное значение 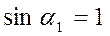и максимальный радиус скрещения пучка электронов с максимальными энергиями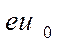

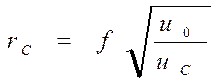, (3.44)

где 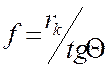- расстояние от поверхности катода до плоскости скрещения (фокусное расстояние).

Выражение (3.44) показывает, что в первом приближении радиус скрещения не зависит от площади иммитирующей поверхности катода и определяется только отношением начальной энергии электронов и энергии электронов в области скрещения.

Поскольку электроны, эмитируемые катодом, имеют максвелловское распределение по скорости, уравнение (3.44) следует рассматривать как уравнение для определения радиуса скрещения, образуемого группой электронов, имеющих энергию 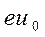и покидающих катод параллельно его поверхности. Очевидно, все электроны, имеющие энергии меньше 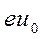и имеют направление, отличное от перпендикулярного к оси, пересекут плоскость скрещения внутри круга с радиусом 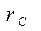. Электроны, имеющие энергию больше 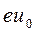, пересекут эту плоскость вне круга с радиусом 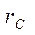. Таким образом, понятие радиус скрещения становится условным, так как среди массы электронов всегда найдутся такие, начальная скорость которых

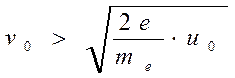(3.45)

Однако доля быстрых электронов будет уменьшаться с увеличением начальной скорости согласно распределению Максвелла. Это приведет к тому, что плотность электронного потока в плоскости скрещивания будет неодинаковой. Наибольшие значения плотности будут на оси системы, по мере удаления от оси плотность будет уменьшаться по экспоненте. Поскольку величину скрещивания усиливают радиусом окружности, вдоль которой плотность тока составляет небольшую (<0,1) плотности тока на оси. Для оценки величины скрещивания необходимо знать распределение плотности тока в скрещивании в зависимости от расстояния от оси. 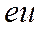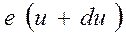Согласно распределению Максвелла число электронов, вылетающих в единицу времени с единицы поверхности катода нормально к ней, приходящегося на единицу телесного угла и обладающих начальной энергией от до равно:

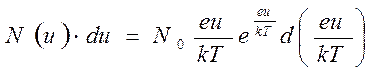, (3.46)

где 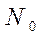- число электронов всех возможных энергий, эмитируемых катодами в единицу времени с 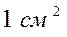своей поверхности нормально к ней в единице телесного угла;

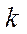- постоянная Больцмана.

Величину 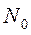можно определить по плотности эмиссионного тока катода

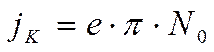. (3.47)

Если предположить, что испускание электронов подчиняется закону Ламберта (это подтверждено экспериментально), то есть допустить, что число элементов в любом направлении пропорционально косинусу угла между нормалью и поверхностью катода и данным направлением, то ток в телесном угле от 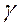до 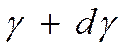будет равен:

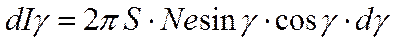, (3.48)

где 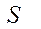- площадь цилиндрической поверхности.

Рассмотрим кольцевую зону в плоскости скрещения, заключенную между двумя окружностями с радиусам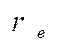и и 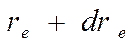. Этой зоне будут соответствовать углы 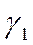и 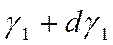. Тогда согласно (3.47) через кольцевую зону будет проходить ток

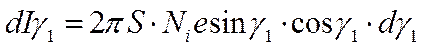, (3.49)

где 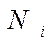- число электронов, эмитируемых катодом с энергиями от 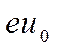до .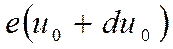

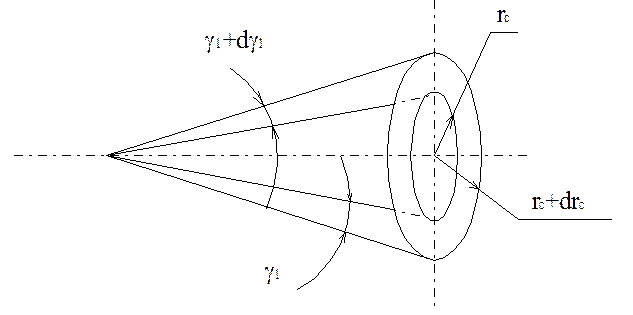Рисунок 3.17 - К выводу плотности тока в кольцевой зоне.

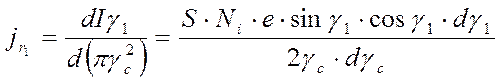(3.50)

Определим 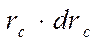из (3.45) и подставим в (3.49). Тогда

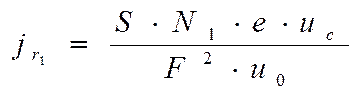(3.51)

Для определения полной плотности тока в скрещивании необходимо просуммировать плотности токов всех скрещений, образуемых электронами с энергиями больше 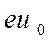(предполагается, что все скрещения формируются в одной плотности). Тогда с учетом максвелловского распределения скоростей получим

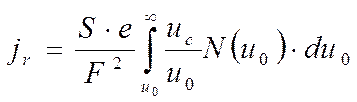. (3.52)

Выразим 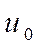из (3.44) и проведем интегрирование

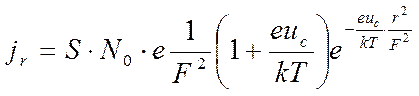(3.53)

Из уравнения следует, что 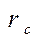убывает с убыванием 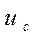. Практически скрещение формируется при 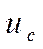не ниже нескольких сот вольт. Считая, что используется катод с 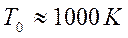можно оценить 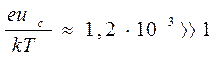. На основании этого можно упростить (3.53):

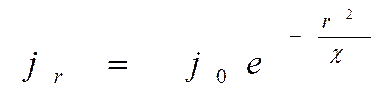, (3.54)

где 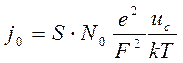плотность тока в центре скрещения 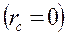; 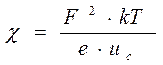- постоянная для заданных условий работы.

Плотность тока в центре скрещения связана с плотностью тока катода 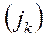уравнением

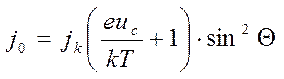(3.55)

Последнее может быть получено из (3.52) при замене 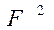на 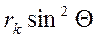(считая, что для малых углов 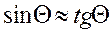) и подстановкой 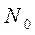из (57).

На основе полученных уравнений можно теоретически оценить 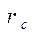, условившись считать границей скрещивания окружность, вдоль которой плотность тока составляет определенную долю плотности тока в центре скрещения. Например, пр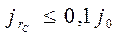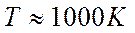и ; и 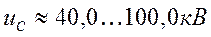, нетрудно получить теоретический радиус скрещения 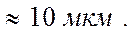Экспериментальная оценка показывает, что радиус пятна намного больше рассчитанного 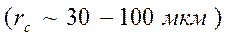, а плотность тока в центре скрещения значительно меньше теоретического. Кроме того, эксперимент показывает, что 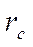не зависит от тока луча только при 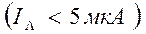. При увеличении 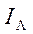, 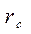заметно увеличивается. Основная причина: не учитывалось искажение электростатического поля собственным зарядом электронного пучка. Пушки Пирса генерируют пучок настолько высокой плотности, что отрицательный пространственный заряд в пучке создает заметную радиальную составляющую электрического поля, вызывающую быстрое расширение пучка, если не принять специальных мер. Методика расчета таких пушек позволяет учитывать влияние пространственного заряда в пучке по траектории электронов. Это дает возможность получать очень высокие плотности тока в пучке при сравнительно невысоких анодных напряжениях и реальных плотностях тока эмиссии катода. Такие пушки применяются в установках для плавки и сварки металлов, а также в различных других установках со сравнительно высокой плотностью энергии в пучке при невысоких анодных напряжениях. Длиннофокусные пушки применяются в случае, когда нужны электронные пучки малого диаметра и высокой удельной энергии. Так как пространственный заряд не позволяет получить пучок с высокой плотностью тока, то пушки, предназначенные для создания пучков малого диаметра (менее 0,1 мм), имеют малую плотность тока в луче. Для сохранения высокой плотности энергии и еще большего снижения влияния пространственного заряда на траектории электронов анодные напряжения в этих конструкциях повышают до 100,0-150,0 кВ, а катоды делают, возможно, меньшего поперечного размера, обычно в виде шпильки из тонкой вольфрамовой или танталовой проволоки.