Распределение концентрации при локальной ИИ

При ионной имплантации через окно в маске шириной 2a (рис. 3.8) распределение концентрации примеси становится двумерным и может быть представлено в виде произведения двух одномерных функций – распределения концентрации примеси в вертикальном (нормальном) направлении C(x) и функции распределения примеси в боковом (латеральном) направлении F(y): C(x, y) = C(x) · F(y), где

,

Здесь DR_py– страгглинг в боковом направлении.

Из рис. 3.8 и последней формулы видно, что при локальной имплантации через окно в маске часть примеси оказывается под краем маски, где она распределяется латерально с характеристической длиной, соответ-ствующей боковому страгглингу DR_py.

Ионное распыление

В силу случайного характера траектории имплатированных ионов часть из них после многократных столкновений с атомами мишени может оказаться вблизи поверхности, передать часть своей энергии приповерхностным атомам и таким образом выбить их из матрицы наружу, т. е. произвести распыление мишени. Скорость ионного распыления U пропорциональна ионному току U = SW j,где S – коэффициент распыления; W – атомный объём материала матрицы. Коэффициент распыления определяется как отношение количества распылённых ионов Q_S к дозе имплантации S = Q_S/Q и зависит от ряда факторов: угла падения пучка ионов j, энергии E, массы атома налетающего иона M_a и атома мишени M_m(рис. 3.9). В первом приближении

.

Зависимость коэффициента распыления от угла падения ионного пучка имеет максимум в области углов j @ 70°. При обычной ионной имплантации с углом j £ 7° распыление не велико и его необходимо учитывать только при больших дозах (токах) имплантации. В этом случае максимум концентрационного распределения с увеличением дозы имплантации приближается к поверхности (рис. 3.10):

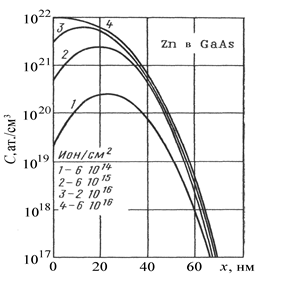
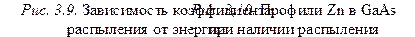
где N_s – концентрация атомов в матрице, до тех пор, пока распределение не станет стационарным, т. е. перестанет изменяться. В этом случае распределение примеси принимает вид

,

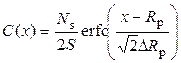а концентрация примеси на поверхности устанавливается C_s ≈ N_s/S.