Уравнение диффузии при термическом окислении

При наличии границы, движущейся со скоростью U, обычное уравнение диффузии с постоянным коэффициентом диффузии D

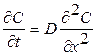
при введении новой координаты y, отсчитываемой от границы (поверхности кремния), y = x – Ut, преобразуется к виду

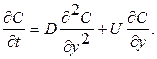
Граничное условие для этого уравнения диффузии выводится из условия баланса примеси на движущейся МФГ. В условиях равновесной сегрегации (С = m_sC_ox), а также при r >>1 изменение количества примеси в прокисленном слое кремния обусловлено диффузионным оттоком примеси в кремний:

dQ – dQ_ox = jdt,

где dQ – количество примеси в прокисленном слое кремния толщиной dx; dQ_ox– количество примеси в образовавшемся слое диоксида кремния шириной dx_ox (dx = adx_ox); j – диффузионный поток примеси из прокисленного слоя в кремний, который по 1-му закону Фика имеет вид

.

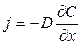Откуда имеем условие

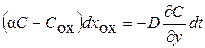
и получаем граничное условие Аталлы–Танненбаум для равновесной сегрегации

.

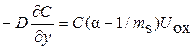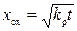При параболическом законе окисления в однородно легированном кремнии устанавливается стационарное распределение концентрации примеси. Оно находится из решения уравнения диффузии при условии 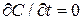и имеет вид:

,

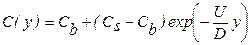где С_b – исходная концентрация примеси в однородно легированном кремнии; С_s – установившаяся концентрация примеси на поверхности кремния (при y = 0).

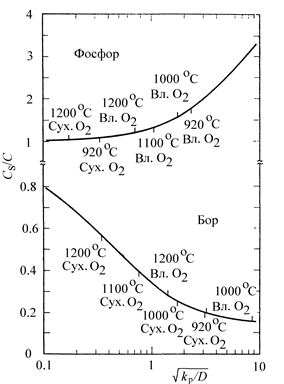
Относительная величина С_s/C_b является функцией отношения k_p/D (рис. 2.5). Как видно из рисунка, для примеси фосфора она увеличивается от 1.1 до 3.4, а для примеси бора падает от 0.8 до 0.15 при увеличении относительной скорости окисления за счёт уменьшения температуры окис-ления от 1200 до 900 °С и изменении среды окисления от сухого кислорода до водяного пара.