Шифр «Модульная арифметика»
Шифр Цезаря
Сообщение S = ДЕНЬ ПРОГРАММИСТА
Дан алфавит:
| А | Б | В | Г | Д | Е | Ж | З | И | Й |
| К | Л | М | Н | О | П | Р | С | Т | У |
| Ф | Х | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э |
| Ю | Я | _ | , | . | ? | ... | |||
| ... |
а) Шифрование: C = f (S,k), например k = +3
Д = 5 5+3=8 Þ З
Е= 6 6+3=9 Þ И
. . .
С = ЗИРЯ?ТУСЖУГППЛФХГ
Примечание: Если сумма символа и ключа превышает длину алфавита, то сумма уменьшается на длину  алфавита (
алфавита ( 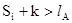 )
)
б) Дешифрование: S = f (C,k)
З = 8 8-3=5 Þ Д
И = 9 9-3=6 Þ Е
. . . S = ДЕНЬ ПРОГРАММИСТА
Примечание: Если при вычитании из номера символа ключа получается отрицательное число или нуль, то необходимо добавить длину алфавита.
в) Криптостойкость. Замена простая – один символ исходника заменяется одним символом шифротекста. Ключевое пространство для данного алфавита от -35 до +35 (-35 £ k £ +35).
Вывод: криптостойкость слабая.
Квадрат Полибия
Весь алфавит укладывается в квадрат. (Данный квадрат 6х6)
| А | Б | В | Г | Д | Е | |
| Ж | З | И | Й | К | Л | |
| М | Н | О | П | Р | С | |
| Т | У | Ф | Х | Ц | Ч | |
| Ш | Щ | Ъ | Ы | Ь | Э | |
| Ю | Я | _ | . | , | ? |
а) Шифрование: C = f (S,КП) = 1516 3255 6334
3533 1435 1131
. . .
б) Дешифрование: S = f (C,КП) Производить действия в обратном порядке.
в) Криптостойкость. Сложная замена:
- один символ исходника заменяется двумя символами шифротекста;
- шифротекст в цифровой форме (алфавит шифротекста в данной ситуации 6 символов – цифр).
Недостаток – нет ключа шифрования.
Вывод: криптостойкость – слабая.
Условные обозначения:
 – алфавит сообщения;
– алфавит сообщения;
S – сообщение, 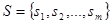 - открытое сообщение;
- открытое сообщение;
 – шифротекст;
– шифротекст;
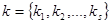 – ключ шифрования;
– ключ шифрования;
 – функция шифрования, где f – криптопреобразование;
– функция шифрования, где f – криптопреобразование;
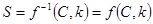 – дешифрование.
– дешифрование.
Шифр «Модульная арифметика»
(квадрат Полибия с ключом)
а) Шифрование 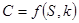
Ключ – слово, содержащее уникальные символы (неповторимые), которые размещаются в начале квадрата, например:
 или
или 
S = ЯХТА_АРХИМЕД 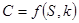
С = 1146 1314 6314 С = 6244 4224 6324
1546 3236 2524 1144 2235 1231
б) Дешифрование 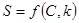
S = ЯХТА_АРХИМЕД
в) Криптографическая стойкость:
- есть ключ. Длина ключа равна 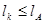 ;
;
- количество ключей – ключевое пространство (все возможные комбинации: если  , то k = n! + (n-1)!+…+2!);
, то k = n! + (n-1)!+…+2!);
- можно использовать шифроблокнот для выбора ключа (две книги – одинаковые и одного издания).
Дата добавления: 2021-03-18; просмотров: 514;











