Ошибка выборочной средней

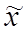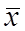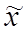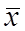Ошибка выборочной средней представляет собой расхождение (разность) между выборочной средней и генеральной средней , возникающее вследствие несплошного выборочного характера наблюдения. Величина ошибки выборочной средней определяется как предел отклонения от , гарантируемый с заданной вероятностью:

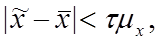
где 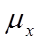– средняя ошибка выборочной средней.

При повторном отборе средняя ошибка определяется следующим образом:

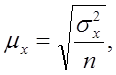
где 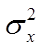– средняя величина дисперсии количественного признака 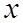, которая рассчитывается по формуле средней арифметической невзвешенной

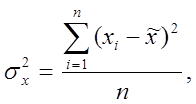
или средней арифметической взвешенной

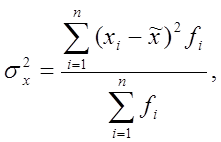
где f_i – статистический вес.

Формулы расчета средней ошибки выборочной средней для различных способов отбора выборочной совокупности приведены в табл.4.2.

Межсерийная дисперсия выборочных средних 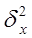и средняя из выборочных дисперсий типических групп 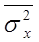вычисляются следующим образом:

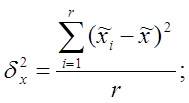
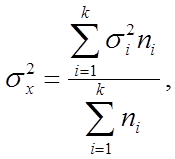
где 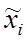– среднее значение показателя в i – й серии;

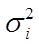– дисперсия признака x в i – й типической группе;

n_i – число единиц в i –й типической группе.

Предельная ошибка выражается следующим образом:

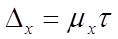
и зависит от вариации изучаемого признака в генеральной совокупности, объема и доли выборки, способа отбора единиц из генеральной совокупности и от величины вероятности, с которой гарантируются результаты выборочного наблюдения.

Средняя величина количественного признака в генеральной совокупности определяется с у четом предельной ошибки выборочной средней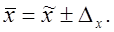

Объем выборки

Определение необходимого объема выборки n основывается на формулах предельных ошибок выборочной доли и выборочной средней. Например, для повторного отбора предельные ошибки равны

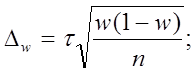
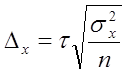
отсюда объемы выборок для расчета выборочной доли n_w и выборочной средней n_x следующие:

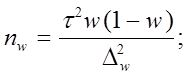
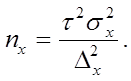
Аналогичным образом определяются объемы выборок при различных способах отбора выборочной совокупности. Для серийного отбора определяется число отобранных серий. Формулы расчета приведены в табл.4.3.

Таблица 4.3

Формулы расчета объема выборки

Метод отбора выборки	Объем выборки или число серий для определения
	выборочной доли	выборочной средней
Механический и собственно–случайный повторный отбор
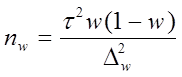
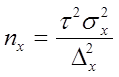
Механический и собственно–случайный бесповторный отбор
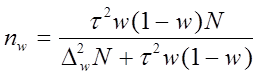
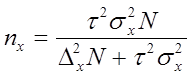
Серийный отбор при бесповторном отборе серий
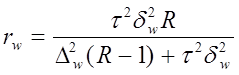
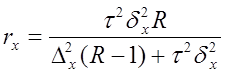
Типический отбор при повторном случайном отборе внутри групп
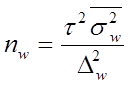
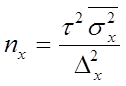
Типический отбор при бесповторном случайном отборе внутри групп

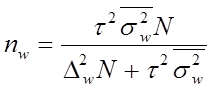
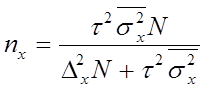
где n_w, n_x – объемы выборок соответственно для определения ошибок выборочной доли и выборочной средней;

r_w, r_x – число отобранных серий соответственно для определения ошибок выборочной доли и выборочной средней;

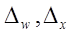– предельные ошибки соответственно выборочной доли и выборочной средней.

Малая выборка

Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 20–30 и может составлять 5–6. С увеличением численности выборочной совокупности повышается точность выборочных данных, однако приходится иногда ограничиваться малым числом наблюдений. Эта необходимость возникает, например, при проверке качества продукции, связанной с уничтожением проверяемой единицы продукции. В математической статистике доказывается, что при малых выборках характеристики выборочной совокупности можно распространять на генеральную, но расчет средней и предельной ошибок выборки имеет особенности.

Ранее указывалось, что при большом объеме выборочной совокупности (n > 100) коэффициент 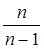, на который необходимо умножить выборочную дисперсию, чтобы получить генеральную, не играет большой роли. Но когда выборочная совокупность небольшая, этот коэффициент необходимо принимать во внимание. Средняя ошибка малой выборки ( 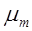) вычисляется по формуле

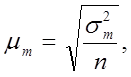
где 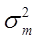– дисперсия в малой выборке, которая определяется следующим образом:

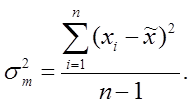
Предельная ошибка имеет вид

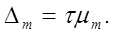
Значение коэффициента доверия 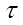зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n . Английский ученый Стьюдент доказал, что в случаях малой выборки действует особый закон распределения вероятности. В табл.4.4 приводятся значения, характеризующие вероятность ( 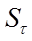) того, что предельная ошибка малой выборки не превысит 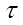–кратную среднюю ошибку:

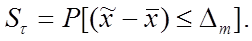
Таблица 4.4

Распределение вероятности 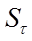в малых выборках в зависимости

от значения коэффициента 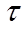и численности выборки

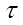
	n
1,0 1,5 2,0 2,5 3,0	0,626 0,792 0,884 0,933 0,960	0,644 0,816 0,908 0,953 0,976	0,657 0,832 0,923 0,966 0,985	0,662 0,838 0,930 0,970 0,988	0,666 0,846 0,936 0,975 0,991	0,668 0,848 0,938 0,977 0,992	0,670 0,850 0,940 0,978 0,993