Энергетические состояния электронов в водородоподобных системах
Водородоподобной называют систему, в которой вокруг ядра с зарядом Zе движется единственный электрон. Строго говоря, отыскание возможных энергетических состояний такой системы является задачей о движении двух частиц около неподвижного центра масс. Однако в силу того, что масса ядра значительно превосходит массу электрона, то можно считать, что ядро неподвижно и движение электрона происходит в его стационарном электрическом поле. При этом сила, действующая на электрон, является кулоновской силой взаимодействия электрических зарядов.
Если принять за ноль потенциальной энергии энергию свободного электрона, т.е. электрона бесконечно удаленного от ядра, то на расстоянии r от ядра электрон обладает потенциальной энергией, равной:
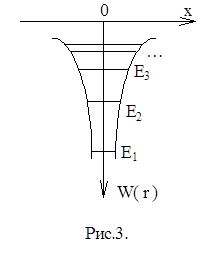
|
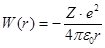 , (20)
, (20)
где Z – порядковый номер химического элемента;
е – заряд электрона;
e0 – удельная диэлектрическая проницаемость среды.
На рис.3 показана кривая W(r). Из этого рисунка видно, что водородоподобную систему можно рассматривать как своеобразную потенциальную яму (потенциальную воронку). Электрон, находящийся в этой яме, обладает отрицательной потенциальной энергией.
Запишем амплитудное уравнение Шредингера для электрона в водородоподобном атоме:
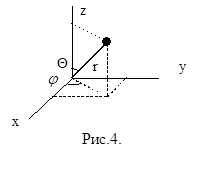
|
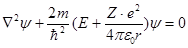 . (21)
. (21)
В силу сферической симметрии потенциальной энергии можно ожидать, что решение рассматриваемой задачи окажется наиболее простым в сферической системе координат (рис.4 ), в которойположение частицы задается расстоянием r от начала координат и углами Q и j. Записав оператор Лапласа в сферической системе координат, получим в этой же системе и уравнение Шредингера:
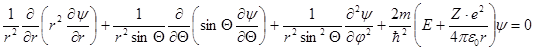 . (22)
. (22)
Следует сказать, что даже в сферической системе координат полное решение данной задачи оказывается чрезвычайно громоздким. Поэтому в дальнейшем мы рассмотрим лишь некоторые частные решения, а также выводы, вытекающин из полного решения.
Первый вывод состоит в том, что электрон в водородоподобном атоме может находиться только в определенных состояниях, которым соответствует дискретный ряд значений его энергии Е, определяемых из уравнения
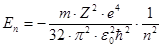 (23)
(23)
подстановкой в него значений главного квантового числа n=1, 2, 3,..
Второй вывод: орбитальный момент количества движения L электрона может принимать лишь следующий ряд дискретных значений
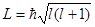 , (24)
, (24)
где 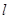 - орбитальное квантовое число, которое может принимать любое значение из следующего ряда
- орбитальное квантовое число, которое может принимать любое значение из следующего ряда 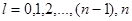 .
.
Третий вывод: вектор орбитального момента количества движения может ориентироваться относительно вектора напряженности внешнего магнитного поля 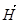 лишь так, что его проекция на направление вектора
лишь так, что его проекция на направление вектора 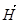 может быть только кратной величине
может быть только кратной величине 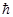 , т.е.
, т.е.
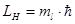 . (25)
. (25)
Число 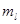 называется магнитным квантовым числом. Оно может принимать все целочисленные значения от
называется магнитным квантовым числом. Оно может принимать все целочисленные значения от 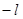 до
до 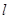 , включая 0:
, включая 0:
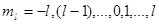
всего 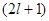 значений.
значений.
|
Пусть 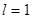 , тогда
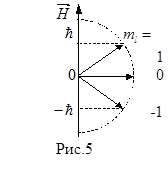
, тогда 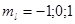 , т.е. имеет три значения, тогда вектор орбитального момента количества движения ориентирован так, как показано на рис.5.
, т.е. имеет три значения, тогда вектор орбитального момента количества движения ориентирован так, как показано на рис.5.
Таким образом, состояние электрона в водородоподобном атоме определяется тремя квантовыми числами – главным квантовым числом n, характеризующим энергию Еn , орбитальным 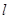 - характеризующим величину орбитального момента количества движения электрона, и магнитным
- характеризующим величину орбитального момента количества движения электрона, и магнитным 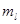 - характеризующим ориентацию вектора орбитального момента количества движения относительно направления внешнего магнитного поля.
- характеризующим ориентацию вектора орбитального момента количества движения относительно направления внешнего магнитного поля.
Однако не все экспериментальные данные согласуются с приведенной выше теорией. Так, например, в спектрах щелочных металлов существуют так называемые дублеты – группы из двух близко расположенных спектральных линий, существование которых не вытекает из решения уравнения Шредингера.
Для объяснения этого явления в 1925 году Гаудсмитом и Уленбеком была выдвинута гипотеза о существовании у электрона собственного момента количества движения. Первоначально предполагалось, что этот момент существует благодаря вращению электрона вокруг собственной оси. Поэтому он получил название спина (от английского «spin» - вращение, веретено). Однако с точки зрения квантовой механики такое представление о спине неверно. Подобно массе и заряду, спин является первичным, неотъемленным свойством электрона (и других частиц), не имеющий аналогов в макромире.
На основании экспериментальных результатов доказано, что спин электрона по абсолютной величине равен:
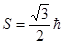 , (26)
, (26)
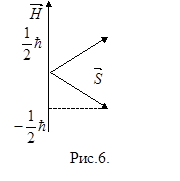
|
а его проекция на направление внешнегомагнитного поля 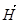 (рис.6) может иметь лишь два значения
(рис.6) может иметь лишь два значения
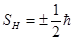 (27)
(27)
или 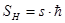 , где
, где 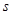 называется спиновым квантовым числом, которое у электрона может принимать лишь два значения:
называется спиновым квантовым числом, которое у электрона может принимать лишь два значения: 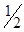 и -
и - 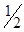 .
.
Итак, с учетом наличия у электрона спина его состояние в водородоподобном атоме задается четырьмя квантовыми числами: главным 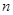 , орбитальным
, орбитальным 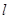 , магнитным
, магнитным 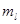 и спиновым
и спиновым 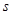 . Энергия же электрона, зависит лишь от значения
. Энергия же электрона, зависит лишь от значения 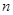 .
.
Если одному и тому же значению энергии (энергетическому уровню) соответствует несколько независимых решений волнового уравнения, то говорят, что имеется вырождение этого энергетического уровня. Кратность вырождения определяют числом таких решений.
В 1925 году Паули установил квантовомеханический закон, названный принципом Паули или принципом исключения. Он гласит: в любом атоме не может быть двух электронов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел: главного 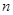 , орбитального
, орбитального 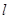 , магнитного
, магнитного 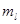 и спинового
и спинового 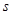 .
.
Применительно к системе электронов в атоме принцип Паули можно записать следующим образом:
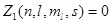 или 1, (28)
или 1, (28)
где 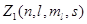 - число электронов находящихся в состоянии, описываемом набором квантовых чисел
- число электронов находящихся в состоянии, описываемом набором квантовых чисел 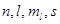 .
.
Пользуясь принципом Паули, можно найти максимальное число электронов в атоме, имеющих заданные значения трех ( 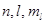 ), двух (
), двух ( 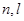 ) и одного (
) и одного ( 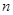 ) квантовых чисел.
) квантовых чисел.
Найдем максимальное число 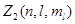 электронов, находящихся в состояниях, определяемых набором трех квантовых чисел (
электронов, находящихся в состояниях, определяемых набором трех квантовых чисел ( 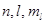 ), т.е. отличающихся лишь ориентацией спинов электронов. Так как число
), т.е. отличающихся лишь ориентацией спинов электронов. Так как число 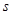 может принимать лишь два значения, т.е.
может принимать лишь два значения, т.е. 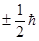 , то имеем
, то имеем
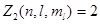 (29)
(29)
Вычислим далее максимальное число электронов 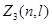 , находящихся в состояниях, определяемых двумя квантовыми числами:
, находящихся в состояниях, определяемых двумя квантовыми числами: 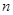 и
и 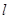 . Так как при заданном числовом значении
. Так как при заданном числовом значении 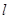 вектор орбитального момента количества движения
вектор орбитального момента количества движения 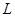 может иметь (
может иметь ( 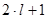 ) различных ориентаций в пространстве, то число электронов равно
) различных ориентаций в пространстве, то число электронов равно
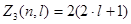 . (30)
. (30)
Значения 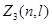 для разных
для разных 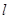 приведены в таблице 1.
приведены в таблице 1.
Таблица 1
Значения орбитальногоквантового числа 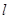
| |||||
| Символ соответствующегосостояния электронов | 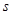
| 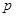
| 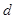
| 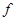
| 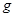
|
Максимальное число электронов 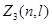
|
Наконец, найдем, пользуясь принципом Паули, максимальное число 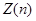 электронов, находящихся в состояниях, определяемых значением
электронов, находящихся в состояниях, определяемых значением 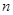 главного квантового числа (или кратность вырождения). Так как
главного квантового числа (или кратность вырождения). Так как 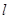 при заданном
при заданном 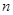 изменяется от 0 до
изменяется от 0 до 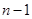 , то суммируя
, то суммируя 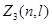 по
по 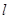 от 0 до
от 0 до 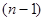 , получим
, получим
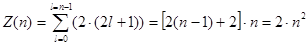 (31)
(31)
В таблице 2, составленной на основе предыдущих формул, приведены максимальные числа электронов, обладающих в атоме заданными значениями квантовых чисел.
Таблица 2
| Заданные квантовыечисла | 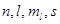
| 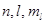
| 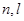
| 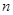
|
| Максимальное число электронов | 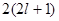
| 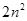
|
В таблице 3 приведены максимальные числа электронов, находящихся в состояниях, характеризуемых данными значениями 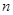 и
и 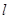 .
.
Таблица 3
| Слой | Число электронов в состояниях | Максимальное число электронов | ||||
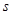
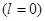
| 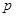 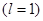
| 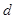
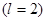
| 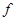
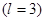
| 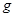
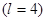
| ||
| K | - | - | - | - | ||
| L | - | - | - | |||
| M | - | - | ||||
| N | - | |||||
| O |
Принцип Паули сыграл выдающуюся роль в развитии современной атомной и ядерной физики. Так, например, удалось теоретически обосновать периодическую систему элементов Менделеева. Без принципа Паули невозможно было бы создать квантовые статистики и современную теорию твердых тел.
Дата добавления: 2016-12-16; просмотров: 1313;











