Расчет зубчатых передач на контактную прочность и изгиб
Перечисленные выше виды разрушения зубьев предупреждают расчетом на прочность по контактным напряжениям (против выкрашивания) и расчетом на прочность при изгибе (против поломки зуба). Изнашивание предупреждают в основном выбором соответствующего материала колес и вида термообработки.
Расчет прямозубых колесзакрытых зубчатых передач напрочность по контактным напряжениям, выполняемый как проектный, ведется по уже известной формуле Герца:
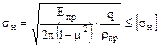
где σн и [σн]- действующие и допускаемые контактные напряжения;
Епр – приведенный модуль упругости,
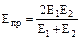 ;
;
здесь Е1, Е2 – модули упругости материала шестерни и колеса;
μ- коэффициент Пуассона;
ρпр - приведенный радиус кривизны
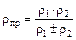 ;
;
здесь ρ1, ρ2 – радиусы кривизны эвольвент зубьев;
q - нормальная нагрузка на единицу длины контактной линии зуба,
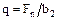
где Fn - равнодействующая сила (см. рис. 13);
b2 -ширина зубчатого венца зубчатого колеса.
Вследствие динамического характера нагружения зубьев и неравномерности распределения нагрузки формула Герца в чистом виде для расчета зубчатых колес дает неверные результаты. Поэтому в нее вводят поправочные эмпирические (опытные) коэффициенты kHα, kHβ, kHv, учитывающие неравномерность распределения нагрузки между зубьями, неравномерность ее распределение по линии контакта зубьев и динамичность нагрузки.
Тогда условие прочности зубьев по контактным напряжениям имеет вид:
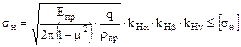 .
.
Важнейшим критерием работоспособности зубчатых передач является прочность зубьев на изгиб Расчет изгибной прочности зубьев проводят в качестве проверочного.
При выводе расчетной формулы принимают допущения
1. Зуб рассматривают как консольную балку, нагруженную сосредоточенной силой Fn, которая вызывает в сечениях зуба напряжения изгиба и сжатия (рис. 16). Силу Fn переносят по линии зацепления NN до оси зуба (в точку О).
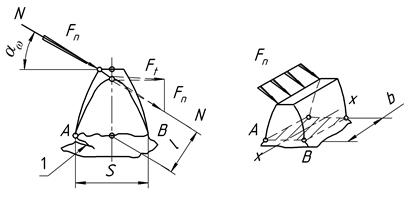
Рис. 16. Схема расчета зубьев на изгиб
(1 – усталостная трещина)
2. Силу трения и напряжения сжатия в расчете не учитывают. При этих допущениях наибольшее напряжение изгиба наблюдается в опасном сечении А-В ножки зуба, расположенном в зоне концентрации напряжений.
Условие прочности зубьев по напряжениям изгиба имеет вид:
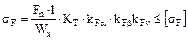 ,
,
где Fn - равнодействующая сила,
Wx - осевой момент сопротивления опасного сечения ножки зуба,
l - плечо изгиба,
Кт - теоретический коэффициент концентрации напряжений,
kFα, kFβ, kFv - коэффициенты неравномерности и динамичности нагрузки,
[σF] - допускаемое напряжение изгиба в опасном сечении зуба.
Прочностные расчеты закрытых косозубых цилиндрических и конических колес проводят аналогично вышерассмотренным расчетам прямозубых цилиндрических колес. Предварительно косозубые цилиндрические и конические колеса приводят к так называемым эквивалентным прямозубым цилиндрическим колесам. Приведение заключается в подсчете числа зубьев эквивалентных колес:
для косозубых цилиндрических колес: 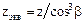
для конических колес: 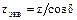
где zэкв - число зубьев эквивалентного прямозубого цилиндрического колеса;
z - действительное число зубьев косозубого цилиндрического или конические колеса;
β - угол наклона зубьев косозубого цилиндрического колеса;
δ - угол конусности конического колеса.
Расчет прочности ведут по формулам для эквивалентных прямозубых передач с введением в них дополнительных поправочных коэффициентов.
Открытые цилиндрические и конические передачи изготавливают с прямыми зубьями. Вследствие повышенного изнашивания их считают прирабатывающимися при любой твердости рабочих поверхностей зубьев.
Размерыоткрытой передачи определяют, исходя из расчета на контактную прочность, с последующей проверкой на изгиб. Причем расчет выполняют аналогично расчетузакрытых прямозубых передач, принимают только другие эмпирические коэффициенты и расчетный модуль увеличивают на 40% (из-за повышенного износа зубьев).
ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
Основные сведения
Червячная передача - это зубчато-винтовая передача, движение в которой осуществляется по принципу винтовой пары (рис 1 в).
Передача состоит из червяка - короткого винта с трапецеидальной резьбой и червячного колеса, имеющего зубья дугообразной формы.
Достоинства червячных передач плавность и бесшумность работы, компактность и сравнительно небольшая масса, возможность получения больших передаточных чисел (до 1000), самоторможение передачи (движение осуществляется только от червяка к колесу).
Недостатки сравнительно низкий КПД вследствие скольжения витков червяка по зубьям колеса, значительное выделение теплоты в зоне зацепления червяка с колесом, повышенное изнашивание и склонность к заеданию.
Червячные передачи широко применяют в подъемнотранспортных машинах и механизмах, где необходима высокая кинематическая точность, в станкостроении, автомобилестроении и др.
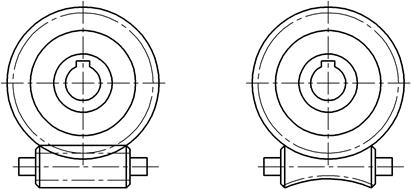
Рис. 17. Схемы червячных передач
В зависимости от формы внешней поверхности червяка (рис. 17) передачи бывают с цилиндрическим (а) и глобоидным (б) червяком. Глобоидная передача имеет повышенный КПД, более высокую несущую способность, но сложна в изготовлении и чувствительна к осевому смещению червяка.
В зависимости от направления линии витка червяка червячные передачи бывают с правым и левым направлением линии витка. В зависимости от числа витков (заходов резьбы) червяка передачи бывают однозаходные и многозаходные.
Червячные передачи бывают с нижним, боковым и верхним расположением червяка относительно червячного колеса. В зависимости от формы винтовой поверхности червяка передачи бывают с архимедовой, конволютным и эвольвентным червяками.
Основными способами изготовления червяков являются: нарезание резцом на токарно-винторезном станке и нарезание модульной (червячной) фрезой на резьбофрезерном станке.
Червячные колеса чаще всего нарезают червячными фрезами, причем червячная фреза представляет собой копию червяка, с которым в последствии будет зацепляться червячное колесо.
Силы, действующие в червячной передаче, изображены на рис. 18.
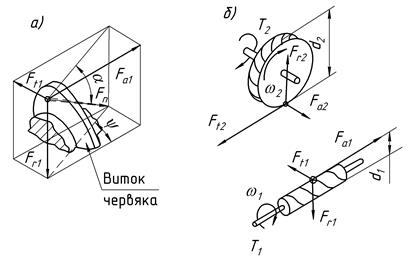
Рис. 18. Схема сил, действующих в червячном зацеплении
Окружная сила на червячном колесе численно равна осевой силе на червяке:
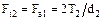 .
.
Окружная сила на червяке численно равна осевой силе на червячном колесе:
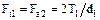 .
.
Радиальная сила на червяке численно равна радиальной силе на колесе:
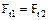
Передаточное число червячной передачи:
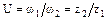
где ω1, z1 – соответственно угловая скорость и число заходов (витков) червячного вала;
ω2, z2 – соответственно угловая скорость и число зубьев червячного колеса.
В червячных передачах расчетным является осевой модуль червяка:
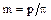 ,
,
где р – делительный осевой шаг витков вала червяка, равный делительному окружному шагу зубьев червячного колеса. Значения расчетного модуля выбирают из стандартных рядов:
1-й ряд:1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0; 12,5; 16,0; 20,0; 25,0.
2-й ряд: 1,5; 3,0; 3,5; 6,0; 7,0; 2,0.
Основные геометрические параметры червячного колеса (рис.19) определяют по формулам:
делительный диаметр 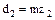 ;
;
модуль m червячного колеса можно определить по формуле:
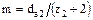
здесь da2 - измеренный диаметр вершин зубьев колеса в среднем сечении,
z2 - число зубьев колеса.
Модуль колеса равен расчетному осевому модулю червяка (округлить до стандартного значения).
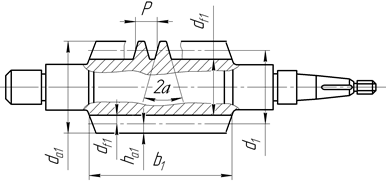
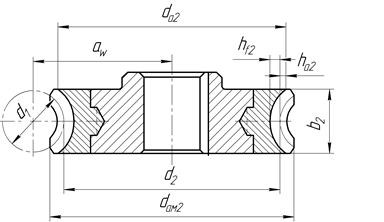
Рис. 19. Основные геометрические параметры червяка и колеса
Диаметр вершин зубьев (в среднем сечении колеса):
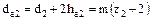
Диаметр впадин зубьев (в среднем сечении колеса):
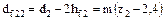
Размеры зубьев колеса по высоте ha2 и hf2 равны соответствующим размерам витков червяка ha1 и hf1.
Основные геометрические параметры червяка находят по формулам:
делительный диаметр 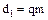
где q – коэффициент диаметра червяка. Значение выбирают из стандартного ряда: 7,1; 8,0; 9,0; 10,0; 11,2; 2,5; 14,0; 16,0; 18,0; 20,0; 22,4; 25,0;
m - осевой модуль червяка (равен модулю колеса).
Высота головки витка червяка 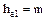 .
.
Высота ножки витка червяка 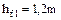 .
.
Диаметр впадин витков червяка 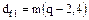 .
.
Диаметр вершин витков червяка 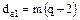 .
.
Дата добавления: 2016-12-16; просмотров: 13510;











