Характеристика эвольвентного зацепления

Чтобы обеспечить постоянство передаточного числа, профили зубьев надо очертить такими кривыми, которое удовлетворяли бы требованиям основной теоремы зацепления.

Теорема: общая нормаль, проведенная через точку касания двух профилей сопряженных зубьев, делит межосевое расстояние (a_w) зубчатых колес на части, обратно пропорциональные их угловым скоростям.

Основным кинематическим условием, которому должны удовлетворять профили зубьев, является постоянство мгновенного передаточного отношения передачи. Этому условию удовлетворяют многие классы кривых. Для обеспечения высокого КПД, прочности и долговечности колес профили должны обеспечивать малые скорости скольжения и достаточные радиусы кривизны в точках контакта. Профили должны допускать легкое изготовление, в частности нарезание простым инструментом независимо от числа зубьев колес.

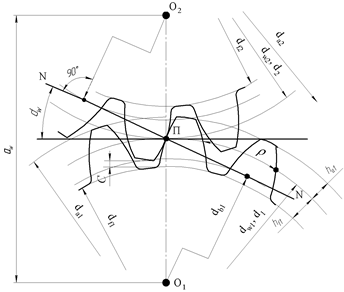
Этим условиям наиболее полно удовлетворяет эвольвентное зацепление, нашедшее широчайшее применение в машиностроении.

Каждое эвольвентное зубчатое колесо должно быть нарезано так, чтобы оно могло входить в зацепление с колесами того же модуля, имеющими любое число зубьев. Эвольвентное зацепление мало чувствительно к отклонениям межосевого расстояния. Эвольвентные зубчатые колеса могут нарезаться простым инструментом: они удобны для контроля.

Зацепление зубчатых колес эквивалентно качению без скольжения окружностей с диаметрами d_w1 и d_w2 (рис. 8), называемых начальными окружностями.

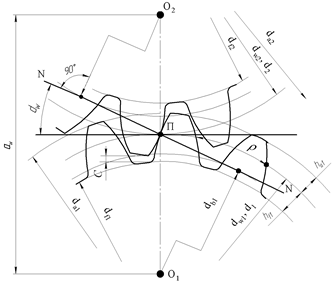
Рис. 8. Образование эвольвентных профилей

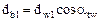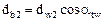При качении без скольжения прямой NN (pис. 8) по основным окружностям с диаметрами и (где 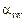- угол зацепления) точки этой прямой описывают на каждом из колес эвольвенты. Поэтому нужное движение колес можно получить зацеплением зубьев, очерченных по эвольвентам. При увеличении числа зубьев до бесконечности эвольвента превращается в прямую, а зубчатое колесо - в рейку с трапециевидным профилем зубьев, удобную для изготовления и контроля. Поэтому в качестве исходного контура для эвольвентного зацепления принята рейка, и широкое применение нашло формообразование зубьев в процессе зацепления с реечным инструментом.

В качестве основного параметра зубчатого зацепления принят модуль зубьев m - величина, пропорциональная шагу р по делительному цилиндру, т. е. цилиндру, на котором шаг зубчатого колеса равен шагу исходного контура, т. е. шагу производящей рейки. Таким образом, .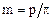

Шаг р, так же как и длина окружности, является кратным числу π и поэтому неудобным для принятия за основной параметр зацепления.

В общем случае для косозубых передач рассматривают окружные и нормальные шаги и соответственно модули.

Окружной делительный шаг р, - это расстояние между одноименными профилями соседних зубьев, измеренное по дуге делительной окружности зубчатого колеса. Очевидно, что 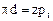откуда .

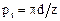Соответственно окружной модуль 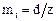т. е. представляет собой частное от деления диаметра делительной окружности на число зубьев.

Нормальный шаг р_n - кратчайшее расстояние по делительному цилиндру между одноименными профильными поверхностями двух смежных зубьев 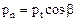, где β - угол наклона линии зубьев по делительному цилиндру.

Соответственно нормальный модуль 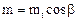. Для прямозубых передач окружные и нормальные шаги и модули соответственно совпадают.

Модули стандартизованы в—диапазоне 0,05...100 мм (ГОСТ 9563—89). Ниже даны модули, мм, в наиболее употребительном диапазоне (1-й ряд следует предпочитать 2-му):

1-й предпочтительный ряд 1; 1,25; 1,5; 2; 2,5;3; 4; 5; 6; 8;

10; 12;16; 20; 25; 32; 40

2-й предпочтительный ряд 1,125; 1,375; 1,75;2,25; 2,75; 3,5; 4,5;

5,5; 7; 9; 11; 14; 18; 22; 28; 36; 45

Для редукторов также допускают модули 1,6; 3,15; 6,3; 12,5 мм.

Для косозубых цилиндрических колесстандартными назначают нормальные модули. Параметры исходного контура цилиндрических зубчатых колес стандартизованы (ГОСТ 13755—81); угол профиля α=20°. Высота головки зуба 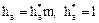. Глубина захода зубьев 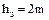; радиальный зазор между зубьями 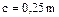(при нарезании долбяками до 0,35m); радиус выкружки у корня зуба 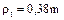(рис. 9 а).

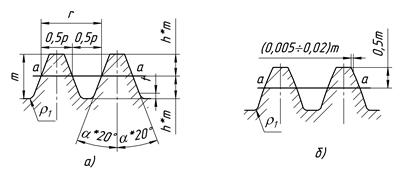
Рис. 9 Исходный контур

Для быстроходных зубчатых передач в целях уменьшения сил удара при входе зубьев в зацепление и выходе их из зацепления и для уменьшения шума применяют модификацию профиля головки зуба (фланкирование). Фланкирование представляет собой преднамеренное отклонение от эвольвенты профиля у вершин зубьев (на части высоты головки), направленное в тело зубьев. Фланкирование уменьшает силы удара, связанные с деформацией зубьев и ошибками основного шага.

Для фланкированных колес предусмотрен исходный контур, у которого каждая боковая сторона зуба очерчена двумя прямыми (рис. 9 б) или прямой и дугой.

Основные геометрические соотношения приведены в таблице 1. Названия и обозначения элементов зубчатого зацепления показаны на рис.10.

Основные кинематические характеристики. Передаточное число равно отношению чисел зубьев колеса z₂ и шестерни z₁: 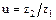, где 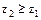и соответственно .

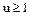Коэффициент торцового перекрытия ε_α равен отношению угла поворота зубчатого колеса от входа в зацепление торцового профиля его зуба до выхода из зацепления, к угловому шагу 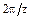. Коэффициент торцового перекрытия в большой степени определяет плавность работы передачи и совместную работу зубьев. Для прямозубых передач он должен обязательно быть больше единицы. Для передач без смещения для определения ε_α можно пользоваться приближенной формулой:

,

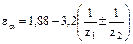где знак «+» для внешнего и «-» для внутреннего зацепления. Для передач со смещением определение ε_α – см. в ГОСТ16532-70.

Удельная скорость скольжения равняется скорости скольжения между зубьями в рассматриваемой точке профиля, деленной на скорость перемещения той же точки профиля зубчатого колеса в направлении скольжения. Эта величина характеризует работу трения на единицу дуги профиля и соответственно ее теплонапряженность.

Таблица 1