Лекция 9. Частные случаи принципа Баейса. Условие Зигерта-Котельникова. Принцип минимакса.

1). Сущность минимаксного принципа.

2). Формирование решающего правила.

Частные случаи байесовского принципа

1) Метод минимального числа ошибочного решений:

Если неизвестна платежная матрица – вынужденно полагают:

С_ij = 1 ;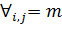

Тогда сгруппируем относительное число правильных решений 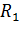и относительное число ошибок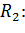

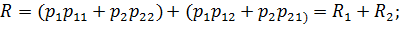
Минимизируем число ошибок:

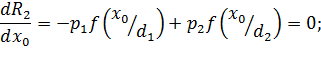
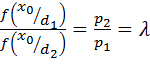- условие Зигерта-Котельникова (условие идеального наблюдения).

Для 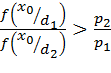- принимают решение d₁.

2) Метод наибольшего правдоподобия.

В условиях предыдущего метода полагают p₁ = p₂ и λ = 1

Тогда при 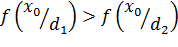принимается решение d₁.

1)Сущность минимаксного принципа.

В практике испытаний нередки случаи, когда вероятности 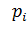неизвестны в силу того, что невозможно сделать достаточно обоснованное предположение о виде закона распределения априорных состояний объекта. Тогда можно предположить, что в процессе испытаний может проявиться самый неблагоприятный случай, когда имеет место сочетание 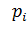, при котором величина риска оказывается максимальной, то есть R= .

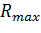Для исследования данного вопроса рассмотрим случай, когда множества Ω, P и D являются двухкомпонентными и платежная матрица задана, причем 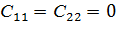, закон f( 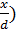задан, вероятность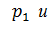 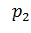неизвестны.

При таких условиях зависимость для байесовского риска имеет вид:

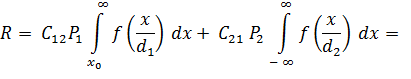
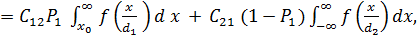(3.1)

т.к. .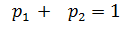

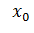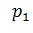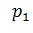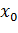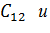
Если зафиксировать значение , то величина риска, как видно, линейно зависит только от неизвестной вероятности . Поскольку в общем случае может изменяться в пределах от а≥0 до в≤1, то эту зависимость нетрудно представить графически, задавшись определенными значениями , 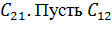=0,5 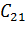, т.е. цена ошибки второго рода вдвое превышает цену ошибки первого рода, и значение 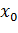определяется из условия равенства вероятностей этих ошибок:

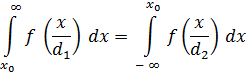
или 1-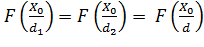

Допущение о равенстве вероятностей ошибок первого и второго рода не нарушает общность дальнейших рассуждений, но облегчает построение и анализ графической зависимости, представленной на рисунке,

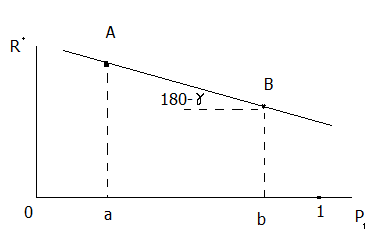
где, ,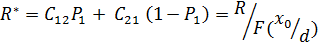

aA= 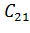, bB=0,5aA

tg 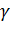= 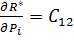- 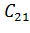= 0,5 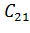- 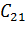= - 0,5 .

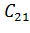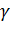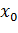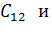
В общем случае tg зависит от параметров , , 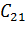так что угол 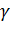может быть как меньше, так и больше 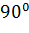(но меньше 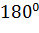). В любом случае при фиксированном 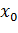линейный характер зависимости R от 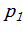сохраняется и 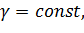откуда следует весьма важный вывод:

если 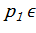[a,b], то величина риска R изменяется от 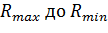(90 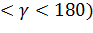или от 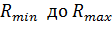( 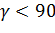), т.е при любом 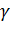риск может достигать максимума, причем в силу линейной зависимости R от 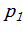экстремум всегда будет граничным и определяется величиной угла .

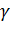В связи с этим естественно задаться вопросом, нельзя ли так повлиять на 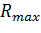, чтобы получить минимальное значение из всех возможных 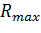. Это оказывается возможным в силу того, что tg 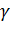зависит от выбираемой нами точки :

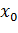tg 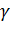= = 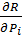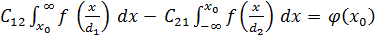(3.2)

Следовательно, варьируя 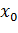, можно влиять на угол 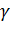и на 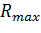, увеличивая или уменьшая это значение.

Значение min 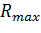будет, очевидно, соответствовать точке 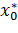определяемой из уравнения:

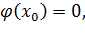(3.3)

т.к. при х 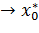величина 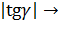0, т.е. А 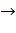В.

Таким образом, сущность принципа минимакса заключается в выборе такого значения граничной точки 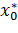, при которой угол 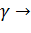0 и, как следствие, 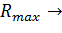min .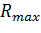

2)Формирование решающего правила

Для формирования решающего правила необходимо установить связь между 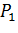и 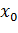, воспользовавшись уравнением:

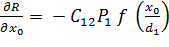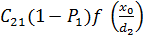+ =0 … (3.4)

Это условие, как было показано, всегда имеет тот смысл, что при известном значении 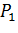определяет точку 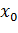, в которой риск достигает минимума. Но в рассматриваемой задаче нет необходимости в поиске такой точки, так как уже установлено, что минимум исследуемой величины 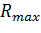достигается при 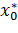. Очевидно, однако, что если в уравнение (3.4) подставить значение 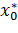, то равенство может быть обеспечено только за счет значения 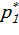, определяемого выражением :

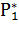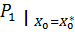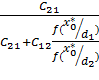= = … (3.5)

Следовательно, выражение (3.5) дает такое значение неизвестной вероятности 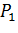, при которой максимальный риск минимизируется:

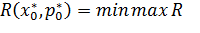
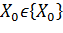
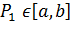
Тогда, =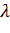

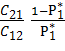
Если опыт дает 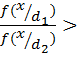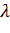,то принимается значение .

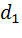Этому решению соответствует величина риска:

= (

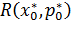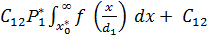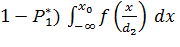
Минимаксное решение– «самое осторожное» решение. Оно применяется в тех случаях, когда принятие неправильного решения приводит к значительным потерям.