Байесовский принцип
Рассмотрим случай, когда технический объект подвергается испытаниям с целью определить возможности его дальнейшего использования. При такой постановке задачи фактически предполагается два возможных состояния объекта:
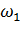 - состояние, допускающие возможности его дальнейшего использования (вероятность p1);
- состояние, допускающие возможности его дальнейшего использования (вероятность p1);
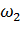 - cостояние, исключающие возможность его дальнейшего использования (вероятность p2).
- cостояние, исключающие возможность его дальнейшего использования (вероятность p2).
Соответственно и множество возможных решений D, будет включать два решения:
d1 - объект находится в состоянии 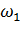 ,
,
d2 - объект находится в состоянии 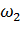 .
.
Пусть объективным признаком возможных состояний является некоторая измеряемая на опыте случайная величина X (например, начальная скорость, износ канала ствола и пр.).
Будем полагать, что закон распределения этой величины известен. При этом для обоих состояний объекта вид закона один и тот же (например, нормальный), но параметры разнятся, так что:
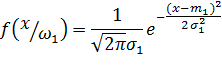
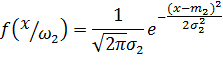
где 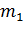 - M[X] в состоянии
- M[X] в состоянии 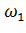 ,
,
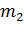 - M[X] в состоянии
- M[X] в состоянии 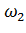 ,
,
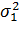 – D[X] в состоянии
– D[X] в состоянии 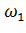 ,
,
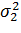 – D[X] в состоянии
– D[X] в состоянии 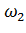 ,
,
Представим плотность 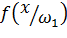 и
и 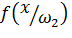 на рисунке:
на рисунке:
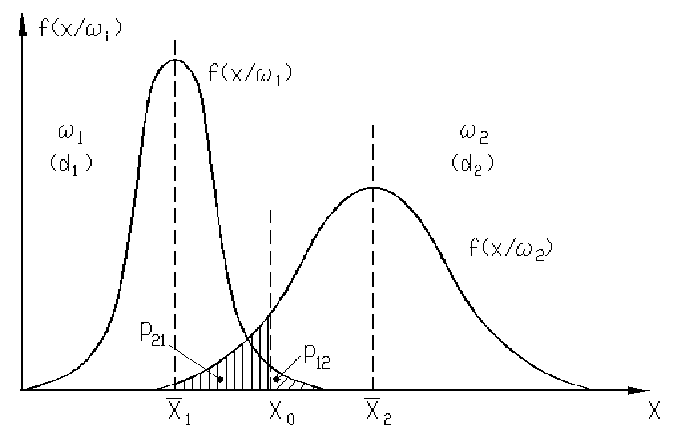
|
Выделим на этом рисунке некоторую граничную точку x0 такую, чтобы при x <x0 преобладающим является состояние w1, тогда надо принимать решение d1, а при x>x0 – w2, которому должно соответствовать решение d2.
Однако, как видно из рисунка, при x>x0 объект может пребывать в состоянии w1 с вероятностью:
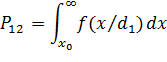
Это вероятность, с которой может быть принято решение d2, хотя объект пребывает в состоянии w1. Цена этого неправильного решения будет С12.
Аналогично при x<x0 может проявиться состояние w2 с вероятностью:
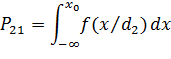
Это вероятность принятия неправильного решения d1, когда в действительности объект находится в состоянии w2. Цена такого неправильного решения будет C21.
В остальных случаях решения будут правильными с ценами С11 и С22 соответственно. Это так называемые «премии» за правильные решения.
Вероятности, с которыми могут появляться премии, равны:
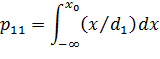
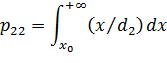
Таким образом, по итогам испытаний могут быть приняты как правильные, так и неправильные решения и функция потерь при этом может быть представлена матрицей вида:
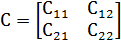
Как было видно, каждый элемент данной матрицы может появиться на практике с определенной вероятностью, то есть матрице C («матрице платежей») ставится в соответствие матрица вероятностей P:
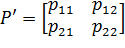
Здесь pij - условные вероятности. Для перехода к безусловным вероятностям надо первую строку матрицы P’ умножить на p1 (вероятность w1), а вторую на p2 (вероятность w2):
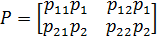
Очевидно, что математическое ожидание C будет некоторой усредненной ценой. Обозначим M[C] = R. Тогда:
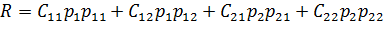 (2.1)
(2.1)
Зависимость (2.1) называется функцией среднего риска. Формально это функция, аргументом которой является величина х0. Естественно потребовать для x0 такого значения, при котором величина R была бы минимальной, то есть заложить условие:
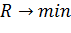 (2.2)
(2.2)
Значение R = Rmin называется байесовским риском.
Правило принятия решений, основанное на байесовском риске, называется байесовским принципом решения на множестве D.
В развернутом виде зависимость (2.1) выглядит следующим образом:
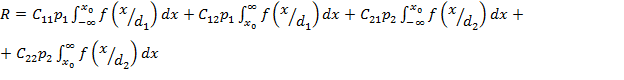
Поэтому:
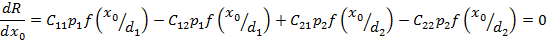
Откуда:
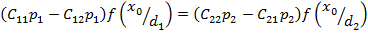
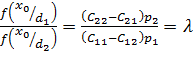 (2.3)
(2.3)
Обычно С11 = С22 и тогда: 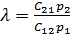 (2.4)
(2.4)
Если 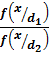 > λ, то x < x0 и принимается решение d1.
> λ, то x < x0 и принимается решение d1.
В общем случае R – функционал:
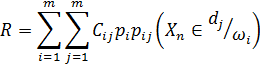
Дата добавления: 2022-05-27; просмотров: 142;











