Дробный факторный эксперимент

1).Минимизация числа опытов. Дробные реплики

2).Выбор полуреплик. Генерирующие соотношения и определяющие контрасты.

Минимизация числа опытов. Дробные реплики.

Количество опытов в полном факторном эксперименте значительно превосходит число определенных коэффициентов линейной модели. Другими словами, полный факторный эксперимент обладает большой избыточностью опытов. Отсюда идея: сократить их число за счет той информации, которая не очень существенна при построении линейных моделей, сохранив при этом оптимальные свойства матрицы планирования. Пути реализации этой идеи рассмотрим на примере плана ПФЭ типа 2²

Запишем матрицу планирования

№ опыта	X1	X2	X1X2	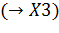Y
	-	-	+
	+	-	-
	-	+	-
	+	+	+

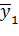
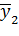
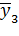
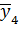
Этот план позволяет вычислить четыре коэффициента и построить модель в виде неполного квадратного уравнения:

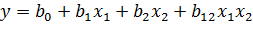
Если имеются основания считать, а что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то можно точно определить три коэффициента: b₀, b₁ и b₂. Остается одна степень cвободы. Употребим ее для сокращения числа опытов. При линейном приближении b₁₂ → 0, тогда вектор столбец X1X2 можно использовать для нового фактора X3. Поставим этот фактор в скобках под столбцом X1X2 и посмотрим, каковы будут оценки коэффициентов регрессии. Оказывается, и мы это определим в дальнейшем, оценки смешаются следующим образом:

b₁ → β₁ + β₂₃ b₂ → β₂ + β₁₃ b₃ → β₃ + β₁₂

Таким образом, здесь уже не будет тех раздельных оценок, которые были в полном факторном эксперименте. Но т.к. постулируется линейная модель, то парные взаимодействия незначимы и такое смешение оценок не имеет практического значения. Вместе с тем появилась возможность построить линейную модель для трех факторов, используя всего четыре опыта вместо восьми, предусматриваемых планом ПФЭ 2³. При этом матрица планирования сохранила все свои основные свойства, в чем нетрудно убедится, анализируя вышенаписанную матрицу. Найденное правило сокращения числа опытов можно сформулировать так:

Чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора определяется знаками этого столбца.

Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной ПФЭ 2³

Эксперимент, в котором реализуется определенная часть всех возможных сочетаний уровней факторов, называется дробным факторным экспериментом (ДФЭ), а соответствующая матрица спектра – дробной репликой. Если реализуется половина всех возможных сочетаний уровней, то матрица называется полурепликой, если четвертая часть – четвертьрепликой и т.д. В общем случае можно рассматривать реплики большей дробности.

Для обозначения дробных реплик, в которых Р линейных эффектов приравненых к эффектам взаимодействия, используется обозначения 2^к-р. Например, полуреплика от плана ПФЭ 2³ обозначается 2^3-1, а четвертьреплика ПФЭ 2⁵ – 2^5-2.

Выбор полуреплик. Генерирующие соотношения и определяющие контрасты.

При построении полуреплики 2^3-1 существуют всего две возможности: приравнять x₃ к “+x₁x₂” или к “-x₁x₂”, как показано в таблице:

Полуреплики 2^3-1

Обе полуреплики равнозначны. Обратим внимание, что для произведения трех столбцов матрицы I выполняется соотношение +1= x₁x₂x₃, а для матрицы II имеем -1= x₁x₂x₃

Символическое обозначение произведения столбцов, равного +1 или -1, называется определяющим контрастом.

Определяющий контраст используется для определения системы смешивания оценок. Для того, чтобы определить какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту. Так, для матрицы I система смешивания будет иметь вид

Для x₁ 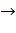x₁=x₁²x₂x₃ = x₂x_3, b₁ → β₁ + β₂₃

Для x₂ 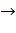x₂=x₁x₂² x₃ = x₁x_3, b₂ → β₂ + β₁₃

Для x₃ x₃=x₁x₂x₃² = x₁x_2, b₃ → β₃ + β₁₂

В случае использования матрицы II получим:

b₁ → β₁ - β₂₃ b₂ → β₂ - β₁₃ b₃ → β₃ – β₁₂

Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генерирующим соотношением.

2^4-1

2³

X₄

X₁ x₂ x₃ x₁x₂ x₁x₃ x₂x₃ x₁x₂ x₃ x₁x₂ x₃ x₁x₂ x₄

1 - - - + + + - - +

2 + - - - - + + - +

3 - + - - + - + - +

4 + + - + - - - - +

5 - - + + - - + + +

6 + - + + - + - + +

7 - + + - - + - + +

8 + + + + + + + + +

+1= x₁x₂x₄

+1= x₁x₃x₄

+1= x₂x₃x₄

+1= x₁x₂x₃x₄

-1= x₁x₂x₄

-1= x₁x₃x₄

-1= x₂x₃x₄

-1= x₁x₂x₃x₄

В данном случае возможны варианты:

1) x₄=x₁x₂

2) x₄=x₁x₃

3) x₄=x₂x₃

4) x₄=x₁x₂x₃

5) x₄= -x₁x₂

6) x₄= -x₁x₃

7) x₄= -x₂x₃

8) x₄= -x₁x₂x₃

Остановимся на 1 и 4 вариантах

Для варианта 1 имеем контраст: +1= x₁x₂x₄

Для варианта 2: +1= x₁x₂x₃x₄

Смешивание оценок для фактора X₁:

Вариант 1: x₁=x₁²x₂x₄ = x₂x_4, b₁ → β₁ + β₂₄

Вариант 2: x₁=x₁²x₂x₃x₄ = x₂x₃x_4, b₁ → β₁ + β₂₃₄

2³ → y = b₀ + b₁x₁+ b₂x₂+ b₃x₃ + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃ + b₁₂₃x₁x₂x₃ ;

Генерирующие соотношения, как видно, формируются путем умножения обеих частей определяющего контраста на соответствующий фактор x₁=x₂x_3, x₂=x₁x₃ и т.д. Здесь первое выражение есть генерирующее соотношение для фактора x₁, второе для фактора x₂ и так далее. Теперь становится ясно, что в таблице 2.7 матрицы различаются по генерирующим соотношениям для вновь введенного третьего фактора, представлены два возможных варианта выбора. С ростом числа факторов растет и число таких вариантов. Так при выборе полуреплики 2^4-1 возможно восемь решений:

x₄=x₁x₂ x₄=x₂x₃ x₄=x₁x₃ x₄=x₁x₂x₃

x₄=-x₁x₂ x₄=-x₂x₃ x₄=-x₁x₃ x₄=-x₁x₂x₃

Как видно, первые шесть полуреплик имеют по три фактора в определяющем контрасте ( +1 = x₁x₂x₄ и т.д.), а две последние по четыре (+1 = x₁x₂x₃x₄, -1= x₁x₂x₃x₄). Это имеет принципиальное значение, т.к. влияет на систему смешивания оценок.

Полуреплики, в которых основные эффекты смешаны с парными взаимодействиями, носят название планов с разрешающей способностью III- по наибольшему числу факторов в определяющем контрасте. Также реплики принято обозначать 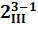, 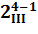и т.д.

Следовательно, две последних полуреплики (седьмая и восьмая) 2^4-1 являются репликами с разрешающей способностью IV: 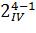. Из всех восьми они имеют наибольшую разрешающую способность и потому называются главными. Они дают такую систему смешивания оценок, при которой линейные эффекты смешаны с эффектами тройного взаимодействия b₁ → β₁ + β₂ β₃ β₄ и т.д. В то время как полуреплики 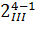дают смешивание линейных эффектов с парными взаимнодействиями: b₁ → β₁ + β₂ β₄ для первой полуреплики и т.д.

В заключение отменим, что сложение двух полуреплик дает план ПФЭ, когда смешивания оценок нет. Наконец, в тех случаях, когда путем замещения вводятся два и более фактора, для определения системы смешивания оценок используется так называемый обобщенный определяющий контраст.

2^5-2

Например, если x₄=x₁x₂x₃ и x₅=x₂x₃, то имеем исходные контрасты

+1= x₁x₂x₃x₄

+1= x₂x₃x₅

Тогда обобщенный контраст определится как соотношение:

1= x₁x₂x₃x₄ = x₂x₃x₅ = x₁x₄x₅,

Где x₁x₄x₅= x₁x₂x₃x₄* x₂x₃x₅.

Поэтому

b₁ → β₁ + β₄₅ + β₂₄₅ + β₁₂₃₅

x₄=x₂x₃ +1= x₂x₃x₄ = x₁x₂x₃x₅ = x₁x₂x₄x₅

x₅=x₁x₂x₃ b₁ → β₁ + β₂₃₅ + β₄₅ + β₁₂₃₄

Проведение эксперимента

1). Реализация плана эксперимента. Ошибки параллельных опытов.

2). Оценка однородности выборочных дисперсий отклика.

Реализация плана эксперимента. Ошибки параллельных опытов.

Реализации плана эксперимента должна предшествовать тщательная подготовка, включающая: сбор и отладку опытной установки, проверку и калибровку измерительных приборов, подготовку исходного сырья, подготовку специального журнала. Журнал оформляют в соответствии с методикой и планом эксперимента так, что бы была ясна последовательность действий. Первую страницу журнала посвящают обычно формулировке цели исследований и характеристике отклика или откликов. На второй странице перечисляются факторы и помещается таблица их уровней и интервалов варьирования, указываются единицы измерения. Матрицы планирования заполняются отдельно с предусмотрением возможности дополнения ее вспомогательными столбцами, сведения которых призваны облегчать анализ и обработку опытных данных. В матрице обязательно должен быть столбец повторных опытов, которые не следует путать с повторными измерениями. При составлении рабочей матрицы целесообразно также включать столбцы для отметки даты проведения опытов и фамилии лаборантов, если опыты производят несколько человек. Отдельные страницы журнала надо отвести для расчетов, связанных с оценкой необходимых для эксперимента ресурсов и анализом полученных после проведения эксперимента результатов.

Первым шагом такого анализа является определение ошибки параллельных опытов. Известно, что повторные или параллельные опыты, т.е опыты, проведения при одних и тех же условиях, не дают полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и надо оценить по параллельным опытам. Для этого опыт воспроизводится в одинаковых условиях n раз и затем определяется среднее арифметическое всех результатов, т.е в каждой строке плана определяется 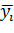. Отклонение результата любого опыта в i-ой строке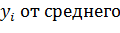 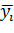есть разница ∆i = 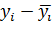. Наличие этой разности свидетельствует об изменчивости значений повторных опытов. Если отклик подчиняется нормальному распределению, эти разности ∆i для всех повторных опытов должны быть статистически однородными. Статистическая однородность означает нахождение реализаций СВ в пределах ее возможных значениях. Поэтому значительное отличие любой из этих разностей от других должно вызывать подозрение либо в нарушении нормального закона распределения отклика, либо в допущении грубой ошибки в регистрации отклика, например, из-за сбоя в работе регистрирующей аппаратуры. В любом случае грубые ошибки должны быть исключены. Для этого можно воспользоваться несколькими критериями, наиболее распространенным из которых является так называемый R-критерий (критерий максимальных отклонений). Его статистика имеет вид:

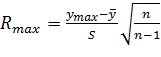или

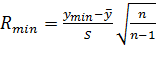
Эти статистики подчиняются r-распределению с числом степеней свободы 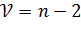, которые при больших n близко к нормальному.

Процедуры использования R-критерия типовые. Рассмотрим их на конкретном примере. Пусть имеется n повторных наблюдений в любой (произвольной) строке плана (поэтому индекс «i» опускаем для упрощения записи): 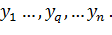Есть подозрение, что одно из наблюдений 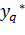несовместимо с остальными. Для проверки достоверности этого факта формируется система гипотез:

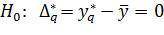
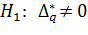
Проверка гипотез осуществляется по R-критерию по общей схеме для случая двухсторонней критической области, для чего вычисляется:

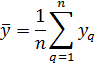
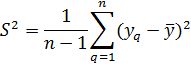
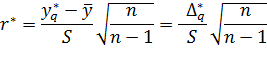
По уровню значимости α и числу степеней свободы 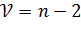определяют критические точки 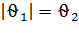. Ес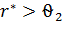ли или 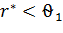,то гипотеза 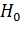отключается и результат 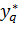считается грубой ошибкой, в силу чего из дальнейшего рассмотрения исключается. В таблицах R-статистики даны критические точки 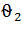для различных уровней значимости. Поэтому на практике ориентируются на модуль разности 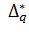. Пример:

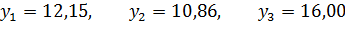
Результат последнего опыта поставим под сомнение. Проверка:

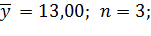
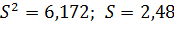
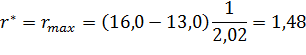
α=0,05; ⟹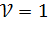

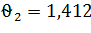
Вывод: т.к. 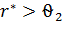, то наблюдение 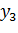может быть признано грубым.

В тех случаях, когда n велико и r-распределение близко к нормальному, можно для исключения грубых отклонений воспользоваться критерием 3σ: если ни одно из наблюдений не выходит за пределы 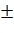3σ (точнее 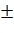3S), то допустимо считать все наблюдения совместными.

Оценка статистической однородности выборочных дисперсий отклика. (Для различных условий эксперимента)

После проверки совместимости результатов повторных опытов будут определены оценки дисперсии отклика во всех строках плана (выборочные дисперсии):

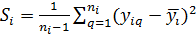
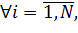
где 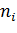- число повторных опытов в i-той строке плана.

Теперь надо проверить статистическую однородность этих оценок, предполагая их взаимную независимость. Сущность проверки сводится к проверке основной гипотезы

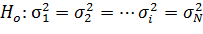
Для этого можно воспользоваться критерием Бартлетта, основанном на статистике:

M= 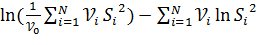(16.1)

где ,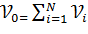

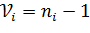
Если гипотеза 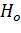верна и все 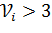, т.е в каждой строке плана проведено хотя бы пять повторных опытов, то отношение

B=M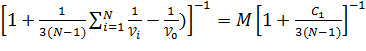

распределено приближено как 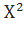с 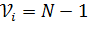степенями свободы.

Так как распределение статистики M не всегда достаточно хорошо аппроксимируется 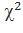- распределением (в частности, такое приближение не является удовлетворительными, если некоторые из 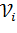равны 1,2 или 3), то для отыскания критических значений М предложены таблицы, основанные на уточнении указанной аппроксимации. Такие таблицы содержатся в сборнике Л.Н Большева и Н.В Смирнова «Таблицы математической статистики», выпущенном издательством «Наука» 1983 г.(Таблицы 4.3а)

Эти таблицы позволяют определить критические точки для уровней значимости α=0,01 и α=0,05 в зависимости от N, а также от

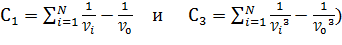(16.2)

Входом в таблицы являются α, N (в указанном сборнике используется обозначение k вместо N ) и C₁. Параметр C₃ вычисляется только в отдельных случаях. Таблицы содержат критические точки для N 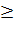3, т.к при N=2 можно воспользоваться критерием Фишера. Прежде чем пользоваться указанными таблицами необходимо ознакомиться с правилами применения критерия Бартлетта, изложенными на с. 47…48 сборника.

Критерий Бартлетта предполагает правостороннюю критическую область. Поэтому, если окажется, что при проверке основной гипотезы расчетное значение статистики М, т.е величина 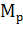, вычисленная по зависимости (16.1), при 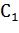, рассчитанном по формуле (16.2), больше критического значения 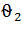, то основная гипотеза отвергается. При этом следует помнить, что если все оценки 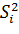получены по выборкам из совокупностей, распределения которых существенно отличны от нормальных, то М-критерий может с большой вероятностью отвергнуть гипотезу 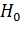, когда она верна.

Если гипотеза 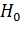принята, то общая оценка дисперсии отклика определяется как средневзвешенная :

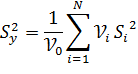
В частном случае, когда число повторных опытов во всех строках плана одинаково, т.е 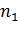= =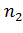…= 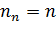, однородность выборочных дисперсий 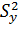можно проверить, используя критерий Кокрена, статистика которого имеет вид:

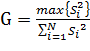(16.3)

Распределение этой статистики связано с двумя числами степеней свободы: 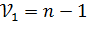и .

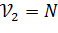Критические значения этой статистики 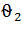(критическая область также правосторонняя) даны в табл. 4.3б вышеуказанного сборника для уровней значимости α=0,05. Входом в таблицы являются величины α, 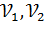, а коментарий к ним изложен на стр. 48…49 сборника. Если при проверке основной гипотезы окажется что G_p, полученное по формуле (16.3), больше 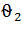, то гипотеза отклоняется. В случае принятия 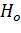общая оценка дисперсии отклика определяется как среднее арифметическое :

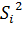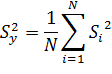
Критерий Кохрена отличается меньшей мощностью, нежели критерий Бартлетта. Поэтому во всех случаях предпочтительнее пользоваться последним.

Если с основной гипотезой 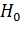конкурирует гипотеза 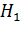, согласно которой одна из дисперсий больше всех остальных, равных друг другу, т.е если

,

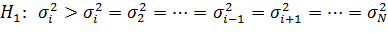причем i заранее неизвестен, то при 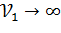мощности обоих критериев будут асимптотически эквивалентными.