Оценка точности результатов равноточных измерений. Арифметическая середина
Если имеется ряд результатов равноточных измерений l1; l2; …; ln одной и той же величины, то за окончательное значение принимают среднюю арифметическую величину L из всех результатов.
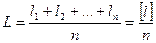 .
.
Если истинное значение измеряемой величины х, то абсолютные ошибки будут равны:
Δ1= l1- х;
Δ2= l2- х;
………;
Δ n= ln- х,
________
[Δ] = [l] – nx.
Из суммы равенств получим, что 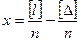 .
.
В соответствии со свойством 4 случайных ошибок, с увеличением числа измерений величина 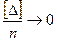 при n → ∞.
при n → ∞.
Следовательно, при бесконечно большом числе измерений, среднее арифметическое L будет стремиться к истинному значению измеряемой величины х.
Величина 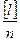 при конечном числе измерений будет вероятнейшим значением определяемой величины, называемой арифметической серединой. Разность между результатом измерения и средним арифметическим называют уклонением от арифметической середины или вероятнейшими ошибками υ, т. е. l1 - L = υ1.
при конечном числе измерений будет вероятнейшим значением определяемой величины, называемой арифметической серединой. Разность между результатом измерения и средним арифметическим называют уклонением от арифметической середины или вероятнейшими ошибками υ, т. е. l1 - L = υ1.
Сумма вероятнейших ошибок равняется нулю 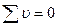 , если величина среднего арифметического не имела округлений.
, если величина среднего арифметического не имела округлений.
В топографии и геодезии в качестве критериев точности измерений в основном применяют среднюю квадратическую ошибку и относительную ошибку.
Среднюю квадратическую ошибку отдельного результата измерения m вычисляют по формуле Гаусса: 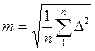 .
.
Формулу Гаусса можно использовать, когда известно истинное значение измеренной величины, а для оценки точности величин, истинное значение которых неизвестно, применяется формула Бесселя 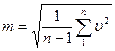 , где υ – вероятнейшая ошибка.
, где υ – вероятнейшая ошибка.
Среднюю квадратическую ошибку арифметической середины М выражают через среднюю квадратическую ошибку m отдельного измерения, т. е. 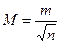 .
.
Таким образом, средняя квадратическая ошибка арифметической середины из результатов равноточных измерений в 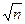 раз меньше средней квадратической ошибки результата отдельного измерения. Для уменьшения ошибки измерения, например, в 2 раза, количество измерений необходимо увеличить в 4 раза.
раз меньше средней квадратической ошибки результата отдельного измерения. Для уменьшения ошибки измерения, например, в 2 раза, количество измерений необходимо увеличить в 4 раза.
Применительно к конкретным условиям указывают критерий отбраковки результатов измерений. В качестве такого критерия служит предельная ошибка. Для наиболее значимых измерений применяются повышенные требования к точности и величину предельной ошибки принимают равной 2m, т. е. Δпр.= 2m (удвоенное значение средней квадратической ошибки. Для менее значимых измерений принимается величина предельной ошибки равная 3m, т. е. Δпр.=3m (утроенное значение средней квадратической ошибки).
Пример, если при угловых измерениях m = 5˝, то «по правилу 2m» отбраковываются все результаты, значения которых по абсолютной величине больше 10˝, а применительно к «правилу 3m» отбраковываются – больше 15˝.
Для суждения о точности многих измерений недостаточно определения величины абсолютной ошибки, необходимо еще знать значение самой измеряемой величины. Так, для получения представления о точности линейных, площадных и других измерений применяется относительная ошибка.
Относительная ошибка – это отвлеченное число, выражающее отношение абсолютной ошибки к результату измерения. Относительную ошибку принято выражать простой дробью, числитель которой равен единице.
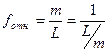 – для отдельного результата измерений
– для отдельного результата измерений
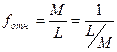 –для арифметической середины.
–для арифметической середины.
Значение знаменателя принято округлять до двух значимых цифр. Чем больше знаменатель, тем выше точность выполненных работ.
Рассмотрим пример. Измерены две линии: одна длиной 220 м со средней квадратической ошибкой 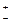 0,17 м, другая – длиной 390 м со средней квадратической ошибкой
0,17 м, другая – длиной 390 м со средней квадратической ошибкой 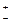 0,23 м, т. е. L1 = 220 м, m1=
0,23 м, т. е. L1 = 220 м, m1= 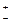 0,17 м, L2 = 390 м, m2=
0,17 м, L2 = 390 м, m2= 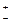 0,23 м. Какая из линий измерена точнее?
0,23 м. Какая из линий измерена точнее?
Подставив результаты измерений и вычислений в вышеприведенные формулы,получим,что относительная ошибка в первом случае будет равна 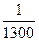 , а во втором –
, а во втором – 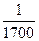 . Следовательно, вторая линия измерена точнее, несмотря на большую величину абсолютной ошибки.
. Следовательно, вторая линия измерена точнее, несмотря на большую величину абсолютной ошибки.
4.5. Оценка точности результатов неравноточных
измерений
При неравноточных измерениях нельзя принимать в обработку среднее арифметическое из результата ряда наблюдений, т. к. необходимо учитывать достоверность каждого результата. Более точные измерения должны оказывать большее влияние на окончательный результат.
Для обработки результатов неравноточных измерений вводят понятие о математическом весе измерения. Вес определяет степень надежности результатов измерений. Чем точнее результат измерений, тем больше его вес. Точность результата измерения характеризуется его средней квадратической ошибкой. Следовательно, чем меньше средняя квадратическая ошибка результата измерения и чем больше его вес, тем надежнее результат.
Таким образом, вес результата измерения р – это величина обратно пропорциональная квадрату средней квадратической ошибки, характеризующей результат данного измерения.
Если ряд неравноточных измерений l1; l2; …; ln, а их средние квадратические ошибки имеют значения m1; m2; …; mn, то соответствующие им веса, будут 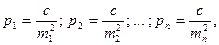 где с – некоторая постоянная величина, число произвольное, но одно и тоже при определении значений всех весов.
где с – некоторая постоянная величина, число произвольное, но одно и тоже при определении значений всех весов.
Обозначим вес среднего арифметического, полученного из n измерений Р, а вес одного измерения – p, тогда 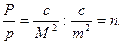
Следовательно, вес арифметической середины в n раз больше веса каждого отдельного результата измерения.
Пусть некоторая величина Х измерена n раз в различных условиях. При этом получены результаты l1 с весом p1 , l2 с весом p2, и т. д. соответственно. Тогда наиболее вероятным значением будет среднее весовое или общее арифметическое среднее (общая арифметическая середина), вычисляемое по формуле 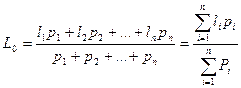 .
.
Общей арифметической серединой или весовым средним неравноточных измерений называется сумма произведений результата каждого измерения на его вес, разделенная на сумму весов.
Истинные значения измеряемых величин, как правило, неизвестны, поэтому при оценке точности результатов неравноточных измерений используют вероятнейшие ошибки.
Средняя квадратическая ошибка единицы веса µ определяется по формуле 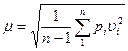 , где υ – вероятнейшая ошибка (уклонение от общей арифметической середины) υ = l – L0 ; n – число измерений.
, где υ – вероятнейшая ошибка (уклонение от общей арифметической середины) υ = l – L0 ; n – число измерений.
Средняя квадратическая ошибка весового среднего или общей арифметической средней М0 вычисляется по формуле 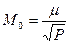 , где Р – сумма весов.
, где Р – сумма весов.
ИЗМЕРЕНИЯ УГЛОВ
Угловые измерения являются одним из основных элементов при выполнении геодезических работ. При создании плановых геодезических сетей и производстве топографических съемок выполняются измерения горизонтальных и вертикальных углов.
Рассмотрим рис. 5.1. Пусть АВС угол на местности, стороны которого не лежат в горизонтальной плоскости. Горизонтальной проекцией этого угла будет угол аВс, полученный проецированием сторон ВА и ВС на горизонтальную плоскость Р. Следовательно, горизонтальный угол аВс – линейный угол, являющийся мерой двугранного угла, образованного вертикальными плоскостями аВВ´А´ и сВВ´С´, проходящими соответственно через стороны ВА и ВС данного угла. Мерой того же двугранного угла будет являться любой другой линейный угол а´в´с´, вершина которого находится на ребре ВВ´ двугранного угла, а стороны в горизонтальной плоскости. Поэтому горизонтальный угол АВС можно измерить с помощью круга, разделенного на градусы и доли градуса, плоскость которого горизонтальна, а центр совмещен с ребром ВВ´ двугранного угла и находится на некоторой удобной для наблюдения высоте в´ относительно точки В. Если деления на круге оцифрованы по ходу часовой стрелки, то угол АВС можно определить как разность отсчетов по кругу, т.е. а´ - с´. Такой круг в геодезии называется лимбом.
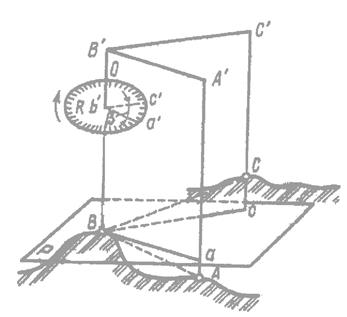
Рис. 5.1.
Для того, чтобы отметить на лимбе отсчеты а´ и с´, необходимо иметь вертикальную плоскость, вращающуюся в центре лимба вокруг вертикальной оси ВВ´. Такая плоскость называется визирной плоскостью.
Изложенный принцип измерения горизонтального угла положен в основу устройства угломерного прибора, называемого теодолитом.
В топографии измеряют углы наклона ν, которые представляют собой вертикальный уголмежду горизонтальной плоскостью и направлением на наблюдаемую точку.
5.1. Теодолиты и их виды. Устройство оптических
теодолитов
Теодолит – это геодезический прибор, предназначенный для измерения на местности горизонтальных и вертикальных углов, а также магнитных азимутов направлений и расстояний по нитяному дальномеру.
Название теодолита (или шифр) состоит из заглавной буквы названия прибора «Т» и цифры после буквы, обозначающей среднюю квадратическую ошибку измерения горизонтального угла в секундах одним приемом, характеризующую сравнительную точность прибора. Последующие модификации теодолитов данной точности получают обозначения, с добавлением новой цифры впереди буквы: 2Т, 3Т. Наличие в названии теодолита буквы «П» говорит о зрительной трубе прямого изображения, а буквы «К» – компенсатора.
Теодолиты классифицируют по конструкции: верньерные и оптические, которые в свою очередь подразделяются на повторительные и неповторительные; и по точности: высокоточные (Т1), точные (Т2, т5) и технические (Т15, Т30, Т–60). Такая классификация принята в России и выпускаемые там теодолиты широко используются в Беларуси.
В настоящее время выпускаются только оптические теодолиты. Рассмотрим устройство теодолита на примере оптического теодолита Т30 и его модификаций (рис. 5.2).
Данный теодолит относится к угломерным прибором технического класса точности. Он состоит из подставки, горизонтального круга, алидады, колонки, вертикального круга, зрительной трубы, отсчетного устройства и уровней.
Для выполнения угломерных работ теодолит устанавливается на штатив. Крепление теодолита к штативу осуществляется при помощи станового винта 10.
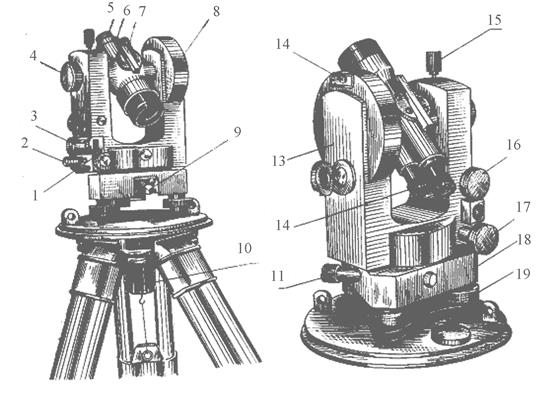
Рис. 5.2
1 – исправительный винт уровня; 2 – закрепительный винт алидады горизонтального круга; 3 – цилиндрический уровень; 4 – кремальерный винт; 5 – окулярное кольцо зрительной трубы; 6 – колпачок, под которым расположены исправительные винты сетки нитей; 7 – зрительная труба; 8 – вертикальный круг; 9 – закрепительный винт горизонтального круга; 10 – становой винт; 11 – наводящий винт горизонтального круга; 12 – отсчетное устройство (микроскоп); 13 – колонка; 14 – паз для установки ориентир-буссоли; 15, 16 – закрепительный и наводящий винты зрительной трубы; 17 – наводящий винт алидады горизонтального круга; 18 – подставка; 19 – подъемный винт.
Подставка (трегер) – нижняя часть теодолита снабжена тремя подъемными винтами и предназначается для горизонтирования прибора. В подставке находится ось горизонтального круга теодолита.
Горизонтальный круг с круговой угломерной шкалой называют лимбом. На шкале через 1˚ нанесены штрихи, которые подписаны по часовой стрелке от 0˚ до 360˚. Лимб наглухо скреплен с его вертикальной трубчатой осью, которая входит во втулку подставки 18. Для вращения в горизонтальной плоскости лимб имеет закрепительный 9 и наводящий 11 винты.
Алидада представляет собой круг, вертикальная ось которой входит в полую ось лимба и таким образом она соединена с ним соосно. Алидада имеет закрепительный 2 и наводящий 17 винты, что позволяет вращать ее в горизонтальной плоскости относительно неподвижного лимба. С алидадой наглухо скреплены колонки 13 и цилиндрический уровень 3. Колонку вместе с алидадой часто называют алидадной частью теодолита.
В колонках теодолита находится его горизонтальная ось, которая наглухо скреплена с вертикальным кругом. Вертикальный круг предназначен для измерения углов наклона и поэтому в отличие от горизонтального имеет секторную оцифровку, т. е. для положения «круг лево» (КЛ) будет иметь знак «+» для положительных углов наклона и знак «-» – для отрицательных. При положении «круг право» (КП) знаки при цифрах будут обратными: оцифровка положительных углов наклона имеет знак «-», а отрицательных – знак «+». Правильный знак угла наклона соответствует положению КЛ. Положение КЛ означает, что вертикальный круг относительно наблюдателя находится слева от зрительной трубы, а при положении КП – справа. Положение вертикального круга меняют переводом зрительной трубы через зенит.
 Зрительная труба 7 также наглухо закреплена на горизонтальной оси прибора и предназначена для визирования на объекты. Она состоит из смотрированных в общем корпусе объектива, фокусирующей линзы, окуляра и расположенной перед ним визирной сетки, которая выгравирована на стеклянной пластинке.
Зрительная труба 7 также наглухо закреплена на горизонтальной оси прибора и предназначена для визирования на объекты. Она состоит из смотрированных в общем корпусе объектива, фокусирующей линзы, окуляра и расположенной перед ним визирной сетки, которая выгравирована на стеклянной пластинке.
Основные штрихи сетки взаимно перпендикулярны, они предназначены для наведения зрительной трубы на объект в горизонтальной и вертикальной плоскостях (рис. 5.3.). Кроме основных штрихов, имеются крайние горизонтальные дальномерные штрихи, предназначенные для определения расстояний по рейке. Для повышения точности визирования половину вертикальной линии сетки нитей наносят в виде близко расположенных параллельных штрихов, называемых биссектором.
 Воображаемая линия, проходящая через центр сетки нитей и оптический центр объектива, называется визирной осью зрительной трубы, а ее продолжение до наблюдаемой точки, образует линию визирования.
Воображаемая линия, проходящая через центр сетки нитей и оптический центр объектива, называется визирной осью зрительной трубы, а ее продолжение до наблюдаемой точки, образует линию визирования.
При наведении зрительной трубы на предмет, наблюдателю необходимо одновременно отчетливо видеть штрихи сетки нитей и наблюдаемый предмет. Отчетливой и резкой видимости сетки нитей по глазу наблюдателя добиваются вращением окулярного кольца 5, а отчетливая видимость предмета достигается путем перемещения фокусирующей линзы кремальерным винтом 4. Для вращения вертикальной плоскости зрительная труба имеет закрепительный 15 и наводящий 16 винты. Таким образом, этими винтами и винтами алидады или лимба зрительную трубу можно наводить на любую точку в пространстве.
Оптические качества зрительной трубы характеризуются увеличением и полем зрения. Увеличение зрительной трубы υ равно отношению угла α, под которым виден предмет в трубу, к углу β, под которым он виден невооруженным глазом 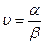 . Зрительная труба теодолита Т 30 имеет увеличение 20х. Поле зрения – угол ограниченный конической поверхностью и видимый через неподвижно установленную трубу (поле зрения Т 30 равно 2˚).
. Зрительная труба теодолита Т 30 имеет увеличение 20х. Поле зрения – угол ограниченный конической поверхностью и видимый через неподвижно установленную трубу (поле зрения Т 30 равно 2˚).
Уровни предназначены для приведения осей или плоскостей геодезических приборов в отвесное или горизонтальное положение. Они бывают цилиндрическими или круглыми. Теодолит Т 30 и его модификации имеют один цилиндрический уровень (рис. 5.4), представляющий собой стеклянную ампулу в оправе заполненную легко подвижной жидкостью (сернистый эфир или этиловый спирт). Внутренняя поверхность ампулы отшлифована и представляет собой дугу постоянного радиуса, а на внешней поверхности нанесены штрихи через 2 мм. «Нуль – пункт» уровня – это средний пункт шкалы. Касательная к пузырьку уровня, когда он находится в нуль-пункте, называется осью цилиндрического уровня. Центральный угол τ, стягивающий одно деление дуги ампулы, называется ценой деления. Цена деления равна 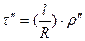 . Таким образом, чем больше радиус кривизны ампулы, тем точнее уровень.
. Таким образом, чем больше радиус кривизны ампулы, тем точнее уровень.
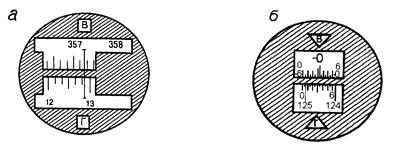
Оптические теодолиты имеют отсчетные устройства (рис. 5.5) в виде штрихового а (Т 30) или шкалового б микроскопов (Т 15; 2 Т 30; 2 Т 30 П).
| 
|
| Рис. 5.4 | Рис. 5.5 |
В поле зрения отсчетных приспособлений одновременно с помощью оптической системы передаются изображения штрихов лимба горизонтального круга, отмеченные внизу буквой «Г» (  ) и изображения штрихов вертикального круга, отмеченные буквой «В» (
) и изображения штрихов вертикального круга, отмеченные буквой «В» (  ). В штриховых микроскопах отсчет берется по неподвижному штриху. Цена одного деления угломерных кругов теодолита Т 30 равна 10΄, десятые доли оцениваются на глаз. Согласно рис. 5.5 а отсчет по горизонтальному кругу (ГК) равен 12˚52΄, а по вертикальному кругу (ВК) – 357˚17΄.
). В штриховых микроскопах отсчет берется по неподвижному штриху. Цена одного деления угломерных кругов теодолита Т 30 равна 10΄, десятые доли оцениваются на глаз. Согласно рис. 5.5 а отсчет по горизонтальному кругу (ГК) равен 12˚52΄, а по вертикальному кругу (ВК) – 357˚17΄.
У теодолита 2 Т 30 П вместо неподвижного штриха в микроскоп вмонтированы неподвижные шкалы для горизонтального и вертикального кругов, длина которых соответствует дуге цены деления лимбов – 1˚. Шкалы разделены штрихами через 5΄ на двенадцать отрезков. Отсчет градусов берется по тому штриху лимба, который находится в пределах шкалы, а минуты определяются по штрихам шкалы слева направо до этого штриха на глаз с точностью до 1΄. Согласно рис. 5.5 б отсчет по ГК равен 125˚06΄.
Шкала для вертикального круга имеет два ряда цифр, в зависимости от угла наклона визирной оси по отношению к плоскости горизонта. При положительных углах наклона отсчет определяется аналогично, как и по ГК. При отрицательных углах наклона (см. рис. 5.5б), когда в пределах шкалы находится штрих вертикального круга со знаком « - » значение минут отсчитывают до этого штриха по шкале справа налево. Согласно рис. 5.5б отсчет по ВК равен минус 0˚27΄.
Поверки теодолитов
Перед проведением полевых угловых измерений необходимо выполнить поверки теодолита, т. е. установить соответствие прибора основным геометрическим условиям, положенных в основу их конструкций. Если геометрические условия не выполняются, то производится юстировка (регулировка) прибора.
Перед началом поверок необходимо провести общий осмотр теодолита. При этом:
1. Оптическая система зрительной трубы должна давать отчетливые изображения.
2. Вращение вертикальной оси теодолита и горизонтальной оси трубы должно совершаться легко и плавно, без заеданий.
3. Все винты (подъемные, наводящие, закрепительные) должны быть исправными, а уровни должны иметь необходимую чувствительность.
К теодолиту предъявляется ряд требований, связанных с взаимным положением его основных осей. Основные оси теодолита (рис. 5.6):
II1 – вертикальная ось (ось вращения алидады горизонтального круга);
НН1 – горизонтальная ось (ось вращения зрительной трубы);
UU1 – ось уровня горизонтального круга (касательная к внутренней поверхности ампулы в нуль-пункте);
VV1 – визирная ось (прямая, проходящая через оптический центр объектива и перекрестие основных штрихов сетки нитей).
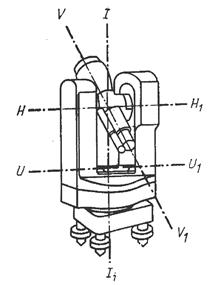
Рис. 5.6
Поверки выполняются в следующем порядке:
1. Ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна вертикальной оси вращения прибора.
Цилиндрический уровень устанавливают по направлению двух подъемных винтов, и вращая их в противоположные стороны приводят пузырек уровня на середину, т. е. в положение нуль-пункт. Затем поворачивают алидаду на 180˚. Если пузырек уровня отклонится с нуль-пункта, то исправительными винтами уровня перемещают его в сторону нуль-пункта на половину дуги отклонения. Поверку повторяют до тех пор, пока пузырек уровня не будет отклоняться от положения «нуль-пункт» более чем на одно деление уровня.
Остальные поверки выполняют после приведения вертикальной оси в отвесное положение. Для этого исправленный уровень устанавливают по направлению третьего подъемного винта, т. е. поворачивают алидаду на 90˚, и вращая этот винт приводят пузырек в нуль-пункт.
2. Визирная ось зрительной трубы должна быть перпендикулярна к ее горизонтальной оси вращения. Отклонение перпендикулярности вызывает коллимационную ошибку с. Зрительную трубу визируют дваждына удаленный хорошо видимый предмет и снимают отсчеты по горизонтальному кругу при двух положениях КЛ и КП. Величину коллимационной ошибки вычисляют по формуле: 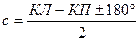 .
.
Колебание значений сдля теодолита Т30 и его модификацийне должно превышать 1΄. В противном случае, для устранения ошибки вычисляется правильный отсчет: 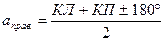 , который устанавливается наводящим винтом алидады. При этом сетка нитей сместится с наведенного предмета. С помощью боковых исправительных винтов перемещают сетку нитей до совмещения с точкой визирования. После исправления коллимационной ошибки поверку необходимо повторить.
, который устанавливается наводящим винтом алидады. При этом сетка нитей сместится с наведенного предмета. С помощью боковых исправительных винтов перемещают сетку нитей до совмещения с точкой визирования. После исправления коллимационной ошибки поверку необходимо повторить.
3. Вертикальный штрих сетки нитей (или биссектор) должен находиться в коллимационной плоскости трубы.
Наводят зрительную трубу на хорошо видимую точку. Наводящим винтом вращают трубу вокруг горизонтальной оси вверх и вниз и следят за изображением наблюдаемой точки. Если вертикальный штрих сетки нитей не отклоняется от изображения точки, то условие поверки считается выполненным. В противном случае отпускают закрепительные винты окулярной части и поворачивают ее, пока вертикальный штрих не займет нужное положение сетки нитей, путем поворота. Эту поверку можно выполнять по подвешенному нитяному отвесу. После этого необходимо повторить вторую поверку.
4. ось вращения зрительной трубы должна быть перпендикулярна к вертикальной оси вращения теодолита.
Теодолит устанавливается в 10–15 м от стены здания и вертикальная ось приводится в отвесное положение. Визируют теодолит на высоко выбранную в стене точку. Опуская зрительную трубу вниз, проецируют эту точку до уровня высоты прибора, т. е. отмечают ее проекцию на стене. Переводят трубу через зенит и при втором положении теодолита наводят на ту же точку, опускают трубу и снова отмечают на стене проекцию перекрестия сетки нитей. Отмеченные проекции точек должны совпасть или не выходить из пределов биссектора. В этом случае условие поверки считается выполненным. В противном случае наклон оси необходимо юстировать в мастерской.
5.3. Установка теодолита и измерение
горизонтальных углов
Для измерения горизонтальных углов на пункте теодолит приводят в рабочее положение, т. е. центрируют и горизонтируют. Кроме этого, устанавливают зрительную трубу по глазу и по предмету.
Центрирование теодолита – это установка вертикальной оси прибора над вершиной измеряемого угла. Выполняется при помощи оптического или нитяного отвеса.
Для этого теодолит на глаз устанавливается над вершиной угла так, чтобы верхняя площадка штатива была приблизительно горизонтальной. Затем, с контролем по отвесу, осторожно заглубляют ножки штатива, пока острие грузика отвеса не окажется над вершиной угла.
Под горизонтированием понимается приведение вертикальной оси прибора в отвесное положение. Для этого выверенный уровень поворотом алидады устанавливают по направлению двух подъемных винтов и вращая их в противоположные стороны приводят пузырек уровня в нуль-пункт. Потом уровень поворачивают на 90˚ и третьим подъемным винтом приводят пузырек к середине. После этого при любом положении алидады пузырек уровня не должен уклоняться от нуль-пункта более чем на одно деление.
Зрительную трубу фокусируют на отчетливую видимость сетки нитей вращением окуляра, а на объект – вращением фокусирующего (кремальерного) винта зрительной трубы.
Горизонтальные углы на местности обычно измеряют двумя способами: способом приемов (способ отдельного угла) и способом круговых приемов (способ В. Я. Струве).
Способ приемов применяется в том случае, когда в точке определяется только один угол между двумя направлениями (табл.5.1). Для исключения влияния коллимационной ошибки и наклона оси вращения зрительной трубы каждый угол измеряют при двух положениях теодолита КП и КЛ. Два полуприема составляют один полный прием.
Таблица 5.1.
| Номер | Отсчеты по горизонтальному кругу | Угол | Среднее из углов | |||||||
| Станции | точки наблюдения | град | мин | с | град | мин | с | град | мин | с |
| II | 07,5 |
Первый полуприем:
1. В вершине измеряемого угла теодолит устанавливается в рабочее положение, направление сторон измеряемого угла обозначается вешками, устанавливаемыми в створах измеряемых линий.
2. Закрепляют горизонтальный круг и перемещая алидаду визируют на нижнюю часть правой (задней) вешки. Точное наведение выполняется наводящими винтами алидады и зрительной трубы. Снимают отсчет по отсчетному устройству и записывают в журнал для измерения углов.
3. Открепив алидаду горизонтального круга, зрительную трубу визируют на нижнюю часть левой (передней) вехи, уточняют и записывают отсчет.
Измеренный угол между двумя направлениями равен разности отсчетов на правую (П) и левую (Л) точки, т. е. β.= П – Л. Причем, если отсчет на заднюю точку меньше, чем на переднюю, то к нему прибавляют 360˚.
Перед выполнением второго полуприема горизонтальный круг смещают примерно на 90˚.
Второй полуприем.
Для этого переводят зрительную трубу через зенит и повторяют измерения угла в том же порядке, что и в первом полуприеме. Результаты измерений записывают в журнал. Расхождение между значениями измеренного угла при КП и КЛ для теодолита Т 30 не должно превышать утроенной точности прибора, т. е. ∆β £ 1,5′.
За окончательный результат принимают среднее арифметическое из двух значений измеренного угла при положении теодолита КП и КЛ, т. е. βср.= 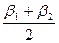 .
.
Для контроля измерений удобно пользоваться способом «от нуля». Совместив нули лимба и алидады, закрепляют алидаду и с открепленным лимбом визируют на левую (переднюю) точку. Закрепив лимб проверяют отсчет по горизонтальному кругу, равному 0˚00΄ и открепив алидаду визируют на заднюю (правую) точку. В этом случае отсчет на правую точку будет равен величине измеряемого угла.
Способ круговых приемовприменяется когда на пункте (станции) необходимо измерить углы по нескольким направлениям, т. е. когда направлений больше двух (табл. 5.2).
Первый прием выполняется при КЛ.
1. Одно из направлений принимают за начальное. Обычно выбирают удаленный пункт с хорошей видимостью. Вращая алидаду устанавливают на лимбе отсчет несколько более 0˚ (например, 0˚05΄). Закрепляют алидаду и винтами горизонтального круга и зрительной трубы визируют на начальное направление. Закрепляют горизонтальный круг, уточняют отсчет и записывают его в журнал измерений.
2. Открепив алидаду, при зафиксированном лимбе последовательно визируют на все другие наблюдаемые точки по ходу часовой стрелки. Снимают отсчеты и записывают их в журнал.
3. Первый полуприем заканчивают повторным наведением и отсчетом на начальный пункт. Сходимость отсчетов при наведении на начальный пункт в начале и конце полуприема называется замыканием горизонта и является необходимым контролем. Расхождение отсчетов не должно превышать утроенной точности прибора.
4. Второй полуприемвыполняется при КП. Открепив алидаду и зрительную трубу, переводят трубу через зенит и визируют на начальный пункт. Снимают и записывают отсчет.
5. Вращая алидаду в обратном порядке, против хода часовой стрелки, наблюдают все остальные пункты. Запись отсчетов в журнале производят снизу вверх. Второй полуприем заканчивают повторным наблюдением на начальный пункт, проверяя сходимость замыкания горизонта.
6. Полевой контроль включает слежение за отсчетами, которые при различных кругах на один и тот же пункт должны отличаться на 180˚. Допустимое расхождение – не более утроенной точности теодолита.
Таблица 5.2
| Станция | Точки визирования | Отсчеты по горизонтальному кругу | Двойная коллимационная погрешность, 2с =КЛ - (КП±180º | Средние отсчеты,
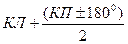 или (КЛ-с)
или (КЛ-с)
| Направление, приведенное к нулевомму | ||
| КЛ | КП | ||||||
| I | Крутая Валун Точка 2 Крутая | 0º08' 38º53' 217º45' 0º09' | 180º09' 218º54' 37º46' 180º10' | Прием 1 -1,0 -1,0 -1,0 -1,0 | 0º08,5' -0,3' 38º53,5' -0,6' 217º45,5' -1,0' 0º09,5' | 0º00,0' 38º44,7' 217º36,4' 0º00,0' | |
| ΔКЛ= +01' ΔКП= +01' | |||||||
При математической обработке журнала полевых измерений вычисляются:
– средняя ошибка незамыкания горизонта по формуле: 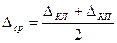 ;
;
– двойная коллимационная ошибка 2с = КЛ–КП ±180˚;
– средний отсчет направления аср=КЛ – с;
– поправки в средние отсчеты за счет незамыкания горизонта 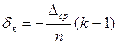 , где n – число наблюдаемых направлений; k – номер по порядку наблюдаемого направления.
, где n – число наблюдаемых направлений; k – номер по порядку наблюдаемого направления.
После этого вычисленные поправки вводятся в средние отсчеты, из которых затем вычитается среднее значение начального направления.
Ошибки измерения горизонтальных углов.К основным источникам погрешностей относятся:
1. Ошибки приборов. Ошибки самих приборов (неточность делений лимба, неперпендикулярность плоскости лимба к основной оси прибора и др.) весьма малы и не оказывают существенного влияния на точность измеряемых углов при измерениях двумя полуприемами.
2. Ошибки измерения угла, возникающие из-за неточности центрирования и визирования. Эти ошибки возрастают с уменьшением сторон угла. Они вызываются неточной установкой теодолита над вершиной измеряемого угла и неправильной постановкой вех. Теодолит необходимо центрировать с точностью 2–4 мм, а вехи – устанавливать отвесно и при измерении углов визировать на их нижнюю часть у поверхности земли.
3. Ошибки от влияния внешней среды. К ним относятся: колебание изображений, нагревание штатива и прибора солнечными лучами, рефракция (преломление световых лучей в земной атмосфере из-за увеличения плотности воздуха к поверхности Земли) и неустойчивость штатива. От прямого воздействия солнечных лучей теодолит и штатив рекомендуется закрывать зонтом.
Дата добавления: 2021-03-18; просмотров: 764;











