Сила давления жидкости на плоские фигуры

Определим силу давления жидкости на дно сосуда. Предположим, что имеются три сосуда разной формы с плоскими днищами одинаковой площади (рис. 10). Уровни воды, налитой в эти сосуды, одинаковы.

Тогда силу давления, действующего на дно сосудов, можно определить Оказывается, что сила давления на плоское горизонтальное дно зависит не от формы сосуда, а только от площади дна и вы-

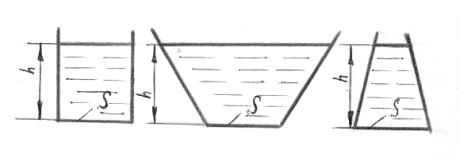
Рис. 10. Гидростатический парадокс

соты уровня жидкости над этим дном. Это положение носит название гидростатического парадокса, потому что при наличии разного количества жидкости в сосудах, сила давления на дно в этих трех сосудах будет одинакова.

Для определения силы давления жидкости на плоскую стенку, произвольно ориентированную в жидкости (рис. 11), следует умножить значение площади стенки на гидростатическое давление в точке центра тяжести стенки.

Сила избыточного давления, создаваемого жидкостью – это вес столба жидкости, основанием которого является площадь стенки, а высотой – глубина погружения центра тяжести стенки

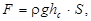(49)

где h_с – глубина погружения центра тяжести стенки;

S – площадь стенки.

Рис. 11. Сила давления на плоскую

фигуру, произвольно ориен-

тированную в пространстве

Если над свободной поверхностью жидкости существует давление р₀, то сила давления будет определена

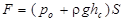. (50)

Иногда при расчётах необходимо определить не только силу давления, но и точку приложения этой силы. Точка приложения силы гидростатического давления называется центром давления. Сила давления, в отличие от силы тяжести, увеличивается с глубиной погружения, и поэтому центр давления будет лежать ниже центра тяжести. Центр давления совпадает с центром тяжести только при горизонтальном расположении плоской фигуры, во всех остальных случаях произвольного расположения фигуры центр давления смещается ниже центра тяжести на расстояние .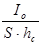

(51)

где 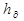– глубина погружения центра давления;

I₀ – момент инерции фигуры относительно горизонтальной оси, которая проходит через центр тяжести;

S – площадь плоской фигуры;

h_c – глубина погружения центра тяжести.

Для прямоугольных фигур глубину погружения центра давления можно принять равной двум третям от полной высоты погруженной фигуры, так как момент инерции для прямоугольников 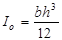, площадь прямоугольника S= b h, а глубина погружения центра тяжести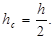

.

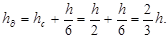(52)

Закон Архимеда

Рассмотрим вертикальный цилиндр высотой h, площадью основания S, находящийся в погруженном состоянии. При этом верхнее основание погружено на глубину h₁ (рис.12), а нижнее – на глубину h₂.

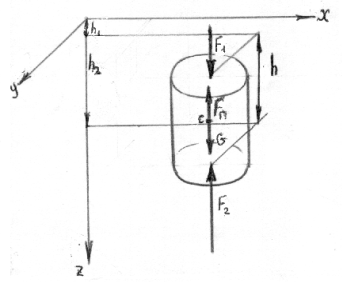
Рис.12. Цилиндр, погруженный в воду

На цилиндр действуют силы:

1. Сила давления на верхнее основание F₁=ρ g h₁ S.

2. Сила давления на нижнее основание F₂=ρ gh₂ S.

3. Силы давления на боковую поверхность цилиндра взаимно уравновешивают друг друга, и поэтому не рассматриваются.

4. Сила тяжести цилиндра G_ц= mg = ρ_ц V g.

Разность сил F₁ и F₂, из которых F₂ всегда больше, так как нижнее основание всегда погружено глубже, называют подъёмной силой (или Архимедовой силой)

F_п=F₂ – F₁=ρ_ж g S (h₂ – h₁)= ρ_ж g S h= ρ_ж g V= m_ж g=G_ж.(53)

То есть подъёмная сила равна весу жидкости, объём которой равен объёмуцилиндра. Отсюда можно сформулировать закон Архимеда: на погруженное в жидкость тело действует сила, направленная вертикально вверх и равная весу объёма жидкости, вытесненной этим телом.

Возможно возникновение трёх случаев:

1. Вес тела цилиндра больше веса вытесненной жидкости (подъёмной силы) G_ц> G_ж и тогда тело тонет.

_2. Вес тела меньше подъёмной силы G_ц<G_ж, и тогда тело всплывает.

3. G_ц=G_ж – тело находится в состоянии равновесия и плавает в погруженном состоянии.

Анализ выражения G_ц^<_>G_ж показывает, что для определения способности тела тонуть или всплывать можно сравнить плотности тела и жидкости.

Выталкивающая (подъемная) сила приложена в центре тяжести вытесненного объёма жидкости, эта точка называется центром водоизмещения . В общем случае центр водоизмещения не совпадает с центром тяжести плавающего тела. Первоочередной задачей в теории плавания является определение плавучести и остойчивости плавающих тел. Плавучестью называется способность тела плавать в полупогруженном состоянии. G_ц < F_п.

Остойчивость – это способность плавающего тела при отклонении от положения равновесия возвращаться в это положение. Положения плавающего тела с креном и без него показаны на рис.13.

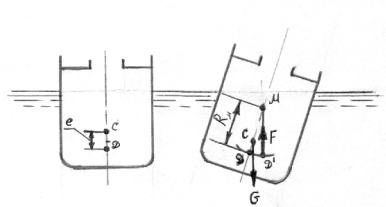
Рис. 13. Плавающее тело без крена и с креном

Здесь С – центр тяжести;

D и D’ – центры тяжести объёма погруженной части в положении без крена и при крене, соответственно;

М – метацентр или же точка пресечения оси плавания с направлением вектора подъёмной силы F при крене;

R_м – метацентрический радиус.

Отрезок СМ – метацентрическая высота.

К плавающему телу прикладываются дополнительные внешние силы, под действием которых тело отклоняется от положения равновесия (ветер, течения, неравномерная нагрузка и т. д.). При исследовании остойчивости судна рассматривают три центра, расположенные на оси плавания. Ось плавания – вертикальная ось, проходящая через центр тяжести судна. Три центра: центр тяжести, центр водоизмещения, метацентр. Два из них не изменяют своего положения при крене (центр тяжести и метацентр), а центр тяжести объёма погруженной части смещается по дуге радиусом R_м с центром в метацентре. Об остойчивости судят по относительному расположению этих центров. Метацентрическая высота всегда должна быть больше нуля. Линия пересечения поверхности воды с боковой поверхностью судна в положении без крена и при полной нагрузке называется грузовой ватерлинией

Объем корпуса судна, расположенный выше грузовой ватерлинии представляет собой запас плавучести. Различают плоскость грузовой ватерлинии и плоскость плавания, которые совпадают только при условии полной загрузки без крена.