Относительный покой жидкости

Относительный покой - это покой жидкости относительно движущегося сосуда, в который жидкость налита. При этом частицы жидкости двигаются вместе с сосудом как одно твердое тело. Для практики представляют интерес три типа относительного покоя:

а) равновесие жидкости в сосуде, который двигается прямолинейно с постоянным ускорением;

б) равновесие жидкости в сосуде, вращающемся с постоянной угловой скоростью вокруг вертикальной оси;

в) равновесие жидкости при вращении сосуда с постоянной угловой скоростью вокруг горизонтальной оси.

а) В первом случае действуют: сила тяжести и горизонтальная сила инерции. Основное дифференциальное уравнение гидростатики упрощается и можно записать

dp =ρ (adx - gdz). Интегрируя, получаем закон распределения давления в жидкости

p_i = p₀ + ρgh_i + ρax_i,(54)

здесь p₀ – давление на поверхности жидкости, ;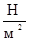

h_i - глубина погружения выбранный точки, м ;

а – линейное ускорение, с которым двигается сосуд, ;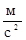

х – линейная координата выбранной точки.

Кроме распределения давления интерес представляет также расположение поверхностей уровня. Поверхностью уровня называется геометрическое место точек с одинаковыми значениями давления. В случае, если из массовых сил действует только сила тяжести, все поверхности уровня жидкости, начиная со свободной поверхности (на которой давление в любой точке p₀), расположены горизонтально. Поверхности уровня (при р = const) описываются уравнением Z = const. В том случае, когда жидкость находится в сосуде двигающемся с постоянным ускорением, поверхности уровня наклоняются к горизонту на угол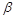

tg 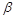= 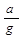.(55)

Поверхности уровня описываются уравнением ax – gz = const

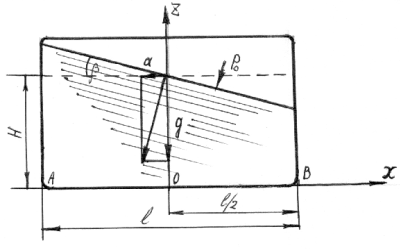
Рис. 14. Равновесие жидкости в сосуде

двигающемся прямолинейно

б) Жидкость налита в сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.

В этом случае на жидкость воздействуют сила тяжести и центробежная силы. Жидкость находится в состоянии покоя относительно сосуда и вращается вместе с ним с той же угловой скоростью.

Проекции массовых сил отнесенных к единице массы на координатные оси x, y, z, будут иметь вид

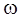А_х = ²х.

А_у = 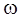²у.,(56)

А_z = g.

где 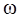- угловая скорость вращения.

Подставляя эти значения проекций массовых сил отнесенных к единице массы в основное дифференциальное уравнение гидростатики (32) получим

dp = r ( 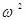x dx + 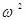y dy + gdz). (57)

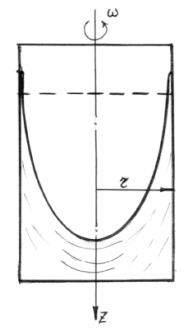
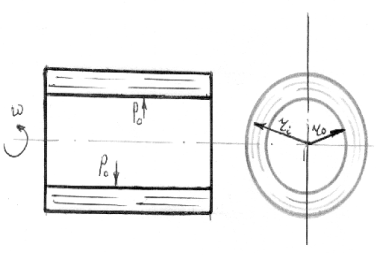
Рис. 15. Сосуд с жидкостью, вращающийся Рис. 16. Сосуд с жидкостью, вращающийся

вокруг вертикальной оси вокруг горизонтальной оси

После интегрирования (57) получаем

p_i = p₀ + rgh_i + 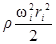. (58)

Уравнение (58) дает возможность определить гидростатическое давление в любой точке жидкости. Поверхности уровня принимают вид параболоидов вращения описываемых уравнением

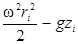= const. (59)

в) При вращении сосуда с жидкостью вокруг горизонтальной оси с постоянной угловой скоростью ускорением свободного падения как правило можно пренебречь. Тогда закон распределения давлений запишется как

p_i = p₀ + 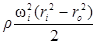. (60)

Поверхности уровня – цилиндрические (рис.14), описываемые уравнением

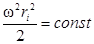. (61)