Основные показатели надежности

Надежность аппарата характеризуется некоторыми количественными показателями.

1. Вероятность безотказной работы – вероятность того, что в определенных

условиях эксплуатации в пределах заданной продолжительности работы отказ не наступит. Вероятность безотказной работы характеризуется статистической оценкой:

P(t) = 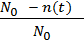, (5.1)

где N₀ – число аппаратов в начале испытания;

n(t) – число аппаратов, отказавших за время t.

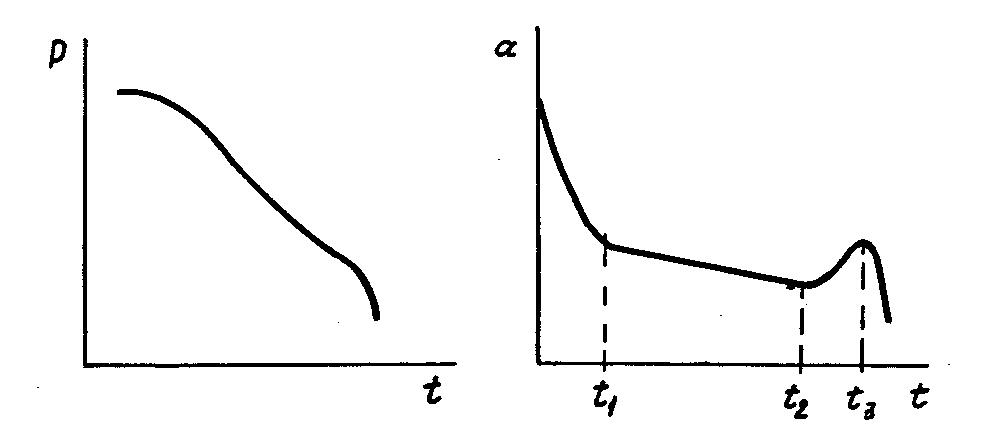
Закон распределения P(t) во времени показан на рис. 5.1, а.

а б

в

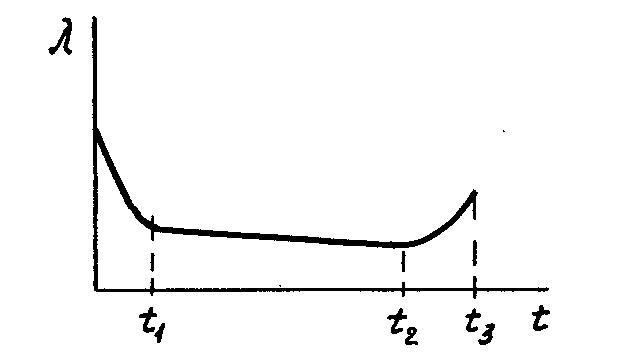
Рис. 5.1. Законы распределения вероятности безотказной работы (а),

частоты отказов (б), интенсивности отказов (в)

Иногда более удобно пользоваться связанной с P(t) величиной – вероятностью отказов. Статистическая оценка вероятности отказа определяется отношением

числа отказавших аппаратов к числу аппаратов в начале испытания:

Q(t) = 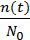= 1 – P(t) . (5.2)

2. Частота отказов – отношение числа отказавших образцов n(t) за данный

отрезок времени Δt к первоначальному числу N₀ , без учета восстановления или замены:

α(t) = 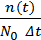. (5.3)

Закон распределения частоты отказов во времени показан на рис. 5.1, б. На первом участке 0 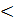t 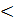t₁, вскрываются производственные дефекты, поэтому частота отказов сравнительно высока. Этот участок является временем приработки. Второй участок t₁ 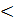t 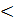t₂ определяет нормальную работу. Третий участок t₂ 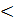t 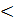t₃ характеризуется возрастанием частоты отказов из-за роста износа аппаратов. После времени t₃ частота отказов уменьшается из-за резкого снижения оставшихся образцов. Частота отказов связана с вероятностью отказов:

α(t) = 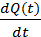. (5.4)

3. Интенсивность отказов – отношение числа отказавших образцов за

время Δt к среднему числу образцов N_ср, исправно работающих, без учета восстановления или замены:

λ(t) = 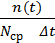, (5.5)

где

N_ср = ,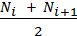

N_i – число аппаратов в начале периода времени Δt;

N_i+1 – число аппаратов в конце периода.

Распределение λ(t) во времени показано на рис. 5.1, в. Здесь можно выделить те же характерные зоны, что и в законе распределения α(t) .

4. Среднее время безотказной работы:

t_ср = 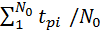. (5.6)

Это математическое ожидание времени безотказной работы.

Все названные критерии имеют вероятностный, статистический характер, поэтому они относятся не к отдельному экземпляру, а к классу устройств. Надо также учитывать, что при сравнении надежности разных устройств необходимо приводить их к одним условиям эксплуатации.