Поперечный профиль каналов
Чаще всего каналы имеют трапециидальную форму поперечного сечения.
Рис. 3.24. Поперечный профиль канала
Поперечным профилем канала называется линия ABCD, пересечения канала с плоскостью, перпендикулярной к направлению сечения. Часть MBCN этого профиля, находящегося под водой, называется смоченным периметром. Его длина обозначается греческой буквой χ (произносится «хи»). Смоченный периметр – это часть периметра живого сечения водотока, соприкасающаяся со стенками и дном русла. Он равен
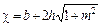 (3.3)
(3.3)
где m – коэффициент откоса (величина характеризующая крутизну откоса);
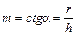 , (3.4)
, (3.4)
где r – заложение откоса; h – глубина воды в канале.
Площадь MBCN, занятая водой называется живым сечением канала и обозначается буквой ω (омега).
ω = (b + mh)h , (3.5)
где b – ширина канала по дну. Ширина канала на уровне воды
В = b +2mh; (3.6)
l– длина откоса. 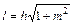 . (3.7)
. (3.7)
Сила трения жидкости о смоченную поверхность зависит от ее площади. Чем больше смоченная поверхность, тем больше при прочих равных условиях сила трения. Для оценки этого влияния в гидравлике широко используется понятие гидравлического радиуса.
Отношение площади живого сечения ω к длине смоченного периметра χ называется гидравлическим радиусом сечения и обозначается буквой R, т.е.
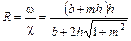 (3.8)
(3.8)
Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности (R ® max при c ® min).
Чем больше смоченная поверхность, тем больше при прочих равных условиях сила трения. Для оценки этого влияния в гидравлике широко используется понятие гидравлического радиуса R. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.
Количество протекающей в единицу времени по каналу воды Q (расход) определяется уравнением
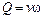 , (3.9)
, (3.9)
причем скорость течения v в свою очередь определяется формулой Шези
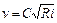 , (3.10)
, (3.10)
где С – коэффициент скорости, зависящий от шероховатости русла;
i – уклон дна канала, равный уклону поверхности потока (равномерное движение). Подставив выражение скорости потока из формулы Шези в формулу расхода получим:
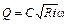 . (3.11)
. (3.11)
Из этой формулы следует, что при данной площади живого сечения ω тот канал пропустит больший расход, у которого при данном уклоне больше гидравлический радиус.
Из формулы R = ω/χ следует, что R ® max при c ® min. Канал такого профиля будет обладать при прочих равных условиях наибольшей пропускной способностью, или иначе сказать, профиль такого канала будет гидравлически наивыгоднейшим.
Как известно из геометрии, из всех фигур минимальным периметром при одной и той же площади обладает круг.
Среди безнапорных потоков таким свойством обладает поток полукруглого сечения (рис. 3.25) гидравлический радиус, которого равен
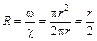 (3.12)
(3.12)
Далее из всех четырехугольных профилей, наивыгоднейшим профилем обладает половина правильного шестиугольника с углом наклона боков к горизонту под углом 60°. Глубина такого канала h = 0,866b, а m = 0,57. Менее выгодным является прямоугольник, как половина квадрата, у которого b = 2h. Можно показать, что и в этих случаях гидравлический радиус равен половине глубины потока[6].
Рис.3.25. Поперечное сечение потоков с гидравлически наивыгоднейшим профилем
На практике выполнение канала такого сечения встречает большие трудности из-за низкой устойчивости боковых поверхностей. Необходимо специальное крепление и т.д. В обыкновенных условиях канал выполняется в виде трапеций с боковыми гранями не круче угла естественного откоса данного грунта, т.к. иначе они будут осыпаться независимо от размывания канала водой.
При трапецеидальном поперечном профиле канала живое сечение канала будет наивыгоднешим в том случае, если соотношение между шириной по дну b и глубиной наполнения h будет
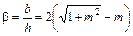 , площадь живого сечения
, площадь живого сечения 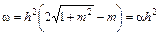 ,
,
а глубина воды в канале 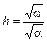 , т.е. гидравлический наивыгоднейший профиль останется только для расчетной глубины наполнения. При всех других наполнениях выгодность такого профиля утрачивается.
, т.е. гидравлический наивыгоднейший профиль останется только для расчетной глубины наполнения. При всех других наполнениях выгодность такого профиля утрачивается.
В осушительных каналах приходиться считаться с большими колебаниями уровней воды, исключающими возможность применения гидравлически выгодных сечений.
Форма поперечного сечения проводящих и оградительных каналов – трапециидальная. Если канал проходит в разных грунтах, то поперечное сечение канала имеет сложный профиль. Откос такого канала имеет переменный коэффициент заложения откосов (рис.3.26).
Разрешается только один перелом откосов. Верхний откос не должен быть положе нижнего.
Рис. 3.26)Схема поперечного сечения канала сложного профиля.
При мощности торфа до 0,7 м перелом откоса не предусматривают.
Ширина проводящих и оградительных каналов по дну определяется расчетом, но не должна быть менее ширины по дну нерасчетных каналов: 0,5 – 0,7 м для магистрального канала; 0,5 м – для валовых; 1,0 м – для оградительных.
Ширину по дну и коэффициент заложения откосов картовых каналов назначаются с учетом принимаемых для строительства и эксплуатации машин (табл.3.7) [7]/
Таблица 3.7
Ширина по дну и коэффициент откоса картовых каналов в зависимости от применяемой для строительства машины
| Наименование машин | Ширина по дну, b, м | Коэффициент заложения откосов m |
| Торфяной экскаватор с профильным ковшом | 0,3 | 0,32 |
| Торфяной экскаватор со штатным ковшом | 0,45 | 0,27(до h = 1,38 м, выше m = 0) |
| Машина для предварительного осушения (типа МТП-37) | 0,1 | 0,375 |
| Машина непрерывного действия (типа МТП-32А) | 0,2 | 0,25 |
Дата добавления: 2021-03-18; просмотров: 743;











