Проводники в электростатическом поле. Электроемкость.

В металлических проводниках концентрация свободных электро­нов достаточно высока, порядка 1028 м-3. Если проводник поместить в электростатическое поле, то произойдет перераспределение свободных электронов, часть из них будет находиться на поверхности проводника, создавая поле, напряженность которого противоположна напряженнос­ти внешнего электростатического поля, установится равновесное состоя­ние (электростатическое равновесие). При равновесии не будет направ­ленного движения электронов, а это означает отсутствие результирую­щего электрического поля внутри проводника, в противном случае свободные заряды постоянно направленно перемещались бы под дейст­вием поля, что противоречит закону сохранения энергии. Так как напряженность поля в проводнике равна нулю, то через лю­бую замкнутую поверхность внутри проводника поток вектора Е равен нулю. Как следует из теоремы Гаусса (10.7.6), алгебраическая сумма электрических зарядов внутри такой поверхности равна нулю. Таким об­разом, несмотря на перераспределение зарядов, концентрация электро­нов равна концентрации положительных ионов. Поэтому удаление внут­ренней части металлического проводника не должно повлиять на раз­мещение зарядов на его поверхности [рис. 10.15; в одинаковых электри­ческих полях расположены одинаковые по форме проводники, но один из них сплошной (а), а другой — полый (б)].

Из формулы (10.6.1) следует, что потенциал всего проводника одинаков, а его поверхность является эквипотенциальной. Следовательно, силовые ли­нии нормальны поверхности проводника (см., например, рис. 10.15).

Таким образом, проводник экранирует внутреннее про­странство от внешних электростатических полей. Эту особенность про­водников используют при электростатической защите. Например, при соответствующих измерениях или для безопасности приборы, лю­дей, животных помещают внутрь металлических проводящих систем, обычно выполненных в виде сетки.

Если источник электрического поля — заряд — находится внутри проводника, то проводник уже не будет экраном, а станет источником электрического поля во внешнем пространстве.

Соединение проводником какого-либо тела с землей называют зазем­лением. При заземлении заряженных проводников, в том числе и тела человека, они теряют заряд и их потенциал будет равен потенциалу зем­ли. Заземление корпусов приборов и аппаратов способствует их безопас­ной эксплуатации, так как исключает возможность для персонала ока­заться под напряжением корпуса аппарата и земли.

Между зарядом и потенциалом проводника существует определенная взаимосвязь. Коэффициент пропорциональности между ними носит название электроемкости. Электроемкость проводника численно равна величине заряда, который нужно сообщить данному проводнику для увеличения его потенциала на единицу:

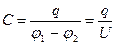
(10.8.1)

Единицей емкости является фарад (1Ф)– емкость такого уединенного проводника,потенциал которогоповышается на 1В при сообщении заряда 1Кл:

1Ф=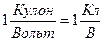

На практике применяется также единицы емкости: 10^-6 фарад = 1 мкФ (микрофарад), 10^-12 фарад = 1 пкФ (пикофарад). Величину емкости любого проводника легко определить, деля величину заряда проводника на его потенциал. Так металлический шар радиуса R, несущий заряд Q, имеет потенциал

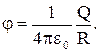
(10.8.2)

Следовательно, его емкость С равна

Для практических целей используется система из двух противоположно заряженных пластин (обкладки), называемая конденсатором. Геометрически это может быть плоская, цилиндрическая или шаровая конфигурация.

Самый простой случай – это плоский конденсатор, который состоит из двух проводящих плоских пластин, пространство между которыми заполнено диэлектриком с проницаемостью ε (рис.10.16.,а). Напряженность поля между пластинами конденсатора

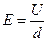
(10.8.4)

где U – разность потенциалов между пластинами конденсатора, d – расстояние между ними.

Если на единице поверхности имеется заряд 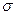и диэлектриком является вакуум, то емкость плоского конденсатора С равна

С = ,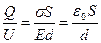

(10.8.5)

где d – расстояние между обкладками конденсатора, S – площадь обкладок конденсатора.

Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостью 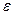, заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то емкость конденсатора

.

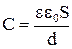(10.8.6)

Известны и другие формы конденсаторов. Так, например, цилиндрические обкладки, разделенные слоем стекла, образуют так называемую лейденскую банку. В экспериментах по наблюдению фотоэффекта часто используется сферический конденсатор(рис.10.16, в), емкость которого

,

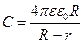(10.8.7)

где R – радиус внешней сферы, r – радиус внутренней сферы. В частном случае, когда внешний радиус R гораздо больше внутреннего r, то емкость сферического конденсатора определяется по следующей формуле:

,

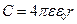(10.8.8)

Емкость цилиндрического конденсатора (рис.10.16, б), состоящего из двух коаксиальных цилиндров длиной L и радиусами r (внутренний) и R (внешний) определяется

,

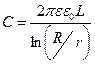(10.8.9)

Если напряжение на конденсаторе сделать слишком большим, то конденсатор «пробивается», т.е. между его обкладками возникает искра (внутри диэлектрика или по его поверхности) и конденсатор портится вследствие нарушения изоляции. Поэтому каждый конденсатор характеризуется не только своей емкостью, но еще и максимальным рабочим напряжением.

Для того чтобы, располагая определенными конденсаторами, осуществить желаемую емкость при нужном рабочем напряжении, конденсаторы соединяются в батареи.

На рис. 10.17. показаны соединения конденсаторов.

При параллельном соединении конденсаторов заряды на всех пластинах складываются и складываются емкости, тогда как потенциалы всех пластин одинакового знака оказываются одинаковыми:

;

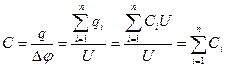(10.8.10)

для последовательного соединения конденсаторовобщее напряжение

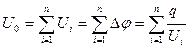
т.к. заряды на всех конденсаторах одинаковы (q=const).

Учитывая, что 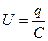, получим

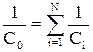
(10.8.11)

В частности, для двух последовательно соединенных конденсаторов общая емкость определяется как:

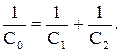
(10.8.12)

Заряженный конденсатор обладает определенной энергией. Энергия электрического поля конденсатора

.

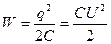(10.8.13)

В однородном поле плоского конденсатора его энергия W должна быть распределена равномерно по всему объему поля V, поэтому используют объемную плотность энергии w, т.е. энергия единицы объема поля, определяемая соотношением

w= = .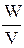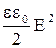

(10.8.14)

Типы диэлектриков

Диэлектриками называют вещества, практически не проводящие электрического тока. В диэлектриках, в отличие от проводников, нет свободных носителей заряда – заряженных частиц, которые могли бы прийти под действием электрического поля в упорядоченное движение и образовать ток проводимости.

Термин «диэлектрик» введен М. Фарадеем для обозначения веществ, через которые проникают электрические поля, в отличие от металлов, внутри которых электростатическое поле равно нулю. К диэлектрикам относят твердые тела, такие, как эбонит, янтарь, фарфор, жидкости (например, чистая вода) и газы при нормальных условиях.

При внесении в электрическое поле каких-либо диэлектриков электрическое поле изменяется. Такую особенность диэлектриков можно пронаблюдать на следующем эксперименте. Приблизим к электрометру какое-либо незаряженное диэлектрическое тело, например толстую стеклянную пластину (рис. 10.18).

Мы увидим, что показания электрометра уменьшаются, когда пластина находится вблизи электрометра, и вновь восстанавливается при удалении пластины.

Если заменить диэлектрик на проводник, то мы будем наблюдать такое же явление. Известно, что на проводнике возникают индукционные заряды, которые и изменяют электрическое поле. Отсюда можно сделать вывод, что и на диэлектрике в электрическом поле также возникают заряды. При этом на ближайшем к телу части диэлектрика появляются заряды, разноименные с зарядом влияющего тела, а на удаленной части диэлектрика – одноименные заряды (рис. 10.18). Появление зарядов на диэлектрике ведет к возникновению сил, действующих на диэлектрики, даже если они первоначально были незаряженными.

Условно выделяют три класса диэлектриков:

1) с полярными молекулами:

2) с неполярными молекулами;

3) кристаллические.

К первому классу относятся такие вещества, как вода, нитробензол и др. Молекулы этих диэлектриков не симметричны, «центры масс» их положительных и отрицательных зарядов не совпадают, и они, подобно диполю, обладают дипольным моментом даже в отсутствие электрического
поля.

На рисунке 10.19 схематически показаны молекулы соляной кислоты (а) и воды (б).

При отсутствии электрического поля дипольные моменты молекул ориентированны хаотически (рис.10.20, а).

В этом случае векторная сумма дипольных моментов всех N молекул равна нулю:

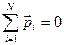
Если полярный диэлектрик поместить в электрическое поле, то дипольные моменты молекул стремятся ориентироваться вдоль линий напряженности поля (рис.10.20, б), однако полной ориентации не будет из-за молекулярно-теплового хаотического движения.

Ко второму классу диэлектриков относятся такие вещества (например, водород, кислород и др.), молекулы которых в отсутствие электрического поля не имеет дипольного момента. В таких молекулах заряды электронов и ядер расположены так, что «центры масс» положительных и отрицательных зарядов совпадают.

Если неполярную молекулу поместить в электрическое поле, то разноименные заряды несколько сместятся в противоположные стороны, и молекула приобретет дипольный момент. На рисунке схематически в виде кружков показаны молекулы такого диэлектрика в отсутствие (рис. 10.21, а) и при наличии поля (рис.10.21, б). Стрелками показано направление дипольных моментов молекул.

Третий класс – кристаллические диэлектрики (например, NaCl), решетка которых состоит из положительных и отрицательных ионов. Такой диэлектрик можно схематически рассматривать как совокупность двух «подрешеток», одна из которых заряжена положительно, другая отрицательно. При отсутствии поля подрешетки расположены симметрично и суммарный электрический момент такого диэлектрика равен нулю. Если диэлектрик поместить в электрическое поле, то подрешетки немного сместятся в противоположные стороны.

При внесении диэлектрика во внешнее электрическое поле происходит поляризация диэлектрика, состоящая в том, что в любом малом его объеме 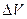возникает отличный от нуля суммарный дипольный электрический момент молекул. Заряды, возникающие на диэлектриках в электрическом поле, называются поляризационными.

Для количественной характеристики поляризации диэлектрика служит специальная физическая величина, называемая поляризованностью (вектор поляризации). Поляризованностью диэлектрика называют электрический момент единицы объема диэлектрика:

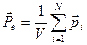(10.9.1)

Единицей поляризованности является кулон на квадратный метр (Кл/м²).

При поляризации диэлектрика на одной его поверхности (грани) создаются положительные заряды, а на другой – отрицательные (рис 10.20, б и 10. 21, б). Эти электрические заряды называют связанными, так как они принадлежат молекулам диэлектрика и не могут перемещаться отдельно от молекулы или быть удалены с поверхности диэлектрика в отличие от свободных зарядов, которых в идеальном диэлектрике нет.

Рассмотрим электрическое поле между пластинами конденсатора, которое характеризуется напряженностью 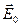(рис.10.22). Внесем в это поле пластину из однородного изотропного диэлектрика. В изотропном диэлектрике поляризация постоянна и не зависит от направления поля.

Смещение зарядов в таких диэлектриках происходит в направлении электрического поля, и поэтому векторы напряженности 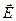и поляризации 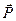параллельны.

Под действием электрического поля диэлектрик поляризуется, и на его поверхности появляются связанные заряды с поверхностной плотностью 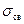. Эти заряды создают внутри пластины однородное поле напряженностью

.

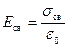Напряженность поля при отсутствии диэлектрика:

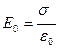
В результате в диэлектрике будет электрическое поле, напряженность которого

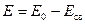(10.9.2)

Поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации, т.е. .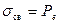

С учетом этого напряженность результирующего поля:

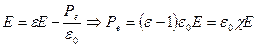, (10.9.3)

Таким образом, вектор поляризации пропорционален напряженности электрического поля в диэлектрике. Величина 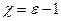называется диэлектрическая восприимчивость среды, которая вместе с диэлектрической проницаемостью характеризует способность диэлектрика к поляризации и зависит от его молекулярного строения, а также от температуры.

Известно, что диэлектрическая проницаемость среды равна отношению силы взаимодействия зарядов в вакууме к силе взаимодействия этих же зарядов на том же расстоянии в среде:

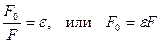
Так как напряженность электрического поля пропорциональна силе, действующей на заряд, то можно записать аналогичное соотношение

,

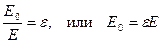т.е. при внесении диэлектрика в электрическое поле его характеристики уменьшаются в ε раз.