Элементы теории потоков применительно к контактной сварке

Основы теории процессов контактной сварки

Тепловые, электрические и диффузионные процессы в металле могут математически рассматриваться как потоки энергии, иногда как потоки частиц или даже как процессы массопереноса.

Для контактной сварки особое значение имеют некоторые характерные поточные дифференциальные уравнения. Одно из них — уравнение теплопроводности Фурье:

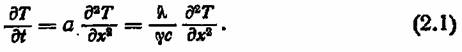
Полностью подобным этому уравнению является уравнение Фика, описывающее процессы диффузии и массопереноса

где С — концентрация вещества в исследуемом объеме; D — коэффициент диффузии, или коэффициент массопереноса.

Дальше следуют два уравнения Максвелла: одно определяет электрическое поле в металле,

другое — магнитное

где Е — электрический потенциал; р — удельное сопротивление среды; μ — магнитная проницаемость; t — время; х — координата; В — магнитная индукция в металле.

Следует подчеркнуть очень существенное обстоятельство. Электрический ток не может существовать без магнитного потока вокруг исследуемого проводящего участка. Основная и главная роль магнитного поля каждого проводящего участка — это сжатие линий протекающего электрического тока. Если речь идет о токе по металлическому проводнику ограниченного сечения, например по стержню, то сжатие его магнитным полем хотя и существует, но оно недостаточно для сжатия линий электрического тока в стержне, а распространение тока по сечению ограничивается габаритными размерами стержня. Если же ток проходит между двумя полюсами по среде неограниченных размеров, и притом в любой среде — металлической, газовой или жидкостной, то магнитное поле не позволит растекаться линиям электрического тока на сколько-нибудь значительное расстояние. Этим определяется, например, существование электрической, в том числе сварочной дуги. Докажем это.

Давление магнитного поля, создаваемого протекающим током в пространстве проводящего участка на линии этого же электрического тока, определяется следующей формулой:

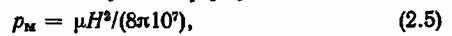
где p_м — давление, МПа; Н — напряженность поля,

d — диаметр проводника, или диаметр круга растекания линий электрического тока. Преобразуя формулы (2.5) и (2.6), получим

Если бы не существовало этого магнитного давления на пространство, занятое дугой, т. е. заполненное горячим газом и плазмой, то под влиянием внутреннего, газового давления (ргаэ = — LRθ) все частицы разлетелись бы в пространство. Число этих частиц, согласно числу Лошмидта, L — 6,02 . 10²⁵ частиц/м3, а давление определяется энергией Rθ. В действительности магнитное давление р_м и газовое р_гаэ уравновешиваются и получается общеизвестное соотношение

откуда видна и причина подъема температуры в так называемой сжатой дуге.

Таким образом, невозможно отрицать эффект сжатия линий электрического тока в неограниченной газовой, даже немагнитной среде. Очень странно в связи с этим отмечать, что факт сжатия линий тока в неограниченной металлической, да еще и магнитной среде некоторые сварщики отрицают до сих пор. Это отрицание реальной действительности приводит иногда к весьма заметным технологическим просчетам.

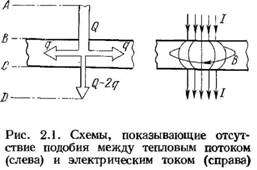
Сравнивая уравнения (2.1)—(2.4), приходится заметить, что они отличаются друг от друга только физическими константами и природой потенциальных функций Т, С, Е и В. Формально, математически, уравнения полностью подобны. Это значит, что при одинаковости начальных и граничных условий решения конкретных задач обеспечиваются одними и теми же математическими функциями от координат и времени. Однако подобие — это не тождество, особенно для процессов физических, разных по своей природе. Для того чтобы внушить осторожность при использовании принципов подобия, достаточно рассмотреть два разных потока, движущихся по одной и той же модели (рис. 2.1). На участках АВ по стержням ограниченных размеров оба потока (Q и I) движутся абсолютно подобно. Как только эти потоки вступают в пространство ВС, т. е. в неограниченную металлическую пластину, электрический ток выходит из этой пластины в область CD таким же по величине, каким он и вошел в нее, какие бы искривления он ни претерпел при этом внутри пластины.

Что касается теплового потока Q, то в пластине он потеряет значительную долю своего потенциала 2q и выйдет из пластины значительно ослабленным. Таким образом, в отличие от стержня в пластине ВС подобия между Q и I нет. Это и понятно: тепловой поток внутри пластины не сжимается никакими силами, а электрический ток сжат магнитным полем В. Как было показано, уравнение теплопроводности Фурье дает безразмерные критерии подобия: Фурье (1.42) и М. В. Кирпичева (1.44).

Уравнения электрического и магнитного полей также имеют критериальное число Максвелла

Для синусоидального переменного тока, поскольку t = 1/f,

где f — частота переменного тока.

Для многих практических электротехнических расчетов академик Л. Р. Нейман ввел несколько видоизмененный критерий, который он назвал символом,

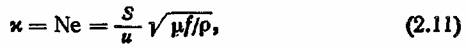
где S — площадь поперечного сечения исследуемого проводника, u — периметр этого сечения.

Формулу (1.36) можно записать в общем виде

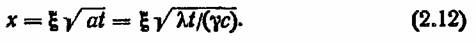
По аналогии с этой записью на основе формулы (2.9) правомерно сделать другую:

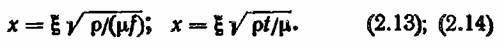
Если из формулы (2.12) видно, чему пропорциональна глубина проникания температуры, то формулы (2.13) и (2.14) показывают, чему пропорциональна глубина проникания электрического тока.

Для практических расчетов используют не полную глубину проникания тока, а только 0,63 от этого размера и называют ее эквивалентной глубиной проникания тока — δ_экв

Если измерять р в Ом . см, t— в с, μ считать безразмерным

числом из отношения

то численно δ_экв определяется по формуле

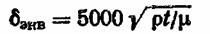
или для переменного тока

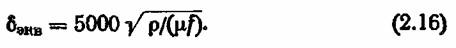
В дальнейшем магнитные величины В и Н будут необходимы для расчетов. Их физический смысл сводится к следующему: на пряженность магнитного поля электрического тока, проходящего по проводнику любого сечения, определяется через периметр этого сечения и

Следовательно, физический смысл понятия напряженности — это число магнитных линий, которое пронизывает воздушное пространство вокруг проводника.

Как известно, воздух немагнитен. Если же вокруг проводника вместо воздуха окажется магнитная сталь, то концентрация магнитных линий в ней получится во много раз большей, чем в воздухе. Такую концентрацию уже называют магнитной индукцией и обозначают символом В.

Таким образом, равенство (2.15) говорит о том, что абсолютная магнитная проницаемость μ представляет собой число, показывающее, во сколько раз магнитных линий в магнитной среде, окружающей проводник, больше, чем в том же объеме, если бы он был немагнитным.

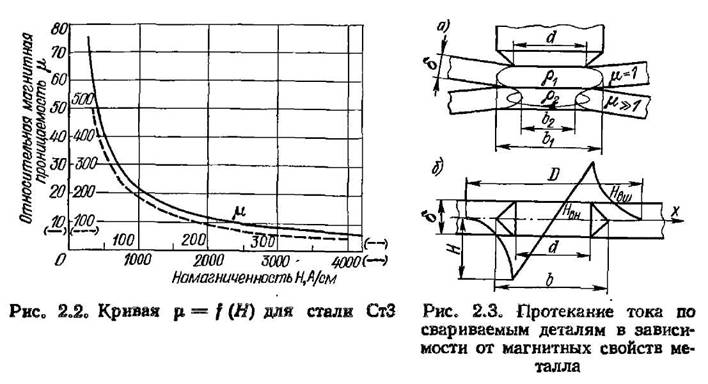
На рис. 2.2 для иллюстрации этой картины представлены кривые В = f (H) для стали СтЗ для воздуха кривая изменения В = f (H) суть прямая под углом 45°.

Рассмотрим теперь картины наиболее достоверного распределения электрического переменного тока по свариваемым деталям различной конфигурации при точечной сварке, что представляет наибольший интерес. На рис. 2.3, а показаны возможные распределения сварочного тока по толщине листов. В верхнем листе из немагнитного металла (μ = 1) не создается большой концентрации магнитного потока вокруг сварочного тока, и его силовые линии могут растекаться на расстояние b₁ > d. Нижний лист из магнитного материала и здесь наблюдается магнитное сжатие тока: b₂ <d.

Если моделировать действительную эллипсоидально-сферическую область в металле, занимаемую током в виде усеченных конусов, то согласно схеме рис. 2.3, б можно написать следующее.

1.Внутренний магнитный поток при напряженности поля определится так:

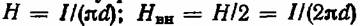
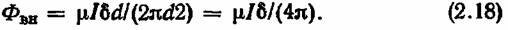
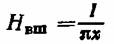
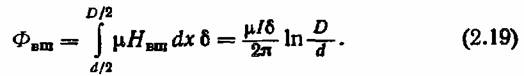
3. Суммарный поток

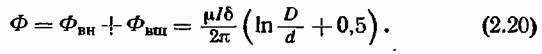
Этот суммарный поток создает в металле индуктивную противоэлектродвижущую силу

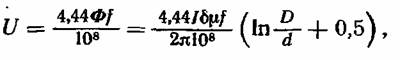
которая эквивалентна падению напряжения на индуктивном сопротивлении (IX).

Академик Л. Р. Нейман установил, что индуктивное сопротивление проводников любой формы определяется формулой

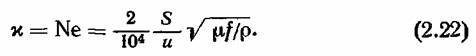
Это сопротивление конусов, которыми моделирует область распространения в металле тока, равно

Учитывая выражение (2.23), запишем

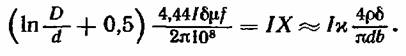
Отношение S/u в данном случае

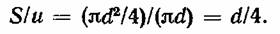
Имея в виду формулы (2.16) и (2.22), определяем

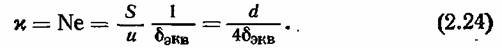
Соответственно

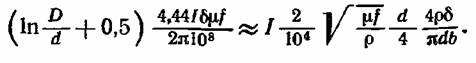
Произведя сокращения и учитывая выражение (2.24), окончательно получаем

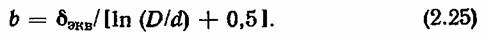
Эта формула весьма существенна. Она показывает, что размер области растекания тока b может быть в действительности и больше и меньше d в зависимости от электрического сопротивления металла при данной температуре и его магнитной проницаемости μ.

Поскольку обе эти характеристики в процессе сварки переменны, то и размер b нестабилен. Формула (2.25) правильно отображает физический смысл токораспределения по сечению металлических листов. Подобно тому как электрический ток, пробивая воздушный зазор между электродами, в первое мгновение концентрируется по стриммеру, совпадающему с осевой линией, он также пронизывает массу металлического листа. Ток возникает по осевой линии электродов в виде тонкого шнура.

Используем формулы этого параграфа для расчета путей протекания тока по листам разной толщины из магнитного металла (СтЗ) и немагнитного титана.

Пример. Толщина свариваемых пластин из СтЗ 3 + 3 мм. Диаметр ядра сварной точки предусмотрим равным dT = 10 мм. Сварочный ток примем I = 12 000 А. Сила сжатия электродов Р = 5750 Н. Напряженность магнитного поля

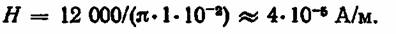
Учитывая величину магнитного поля, по кривой намагничивания стали СтЗ (см. рис. 2.2) находим абсолютную величину относительной магнитной проницаемости μ ≈ 10.

Ширину свариваемой пластины примем D = 40 мм. При этих Данных рассчитываем диаметр круга контактирования в момент включения, т. е. при холодном металле, согласно формуле (1.8),

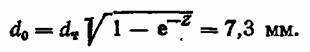
Размер b_о по формуле (2.25) b_о — 4,6 мм.

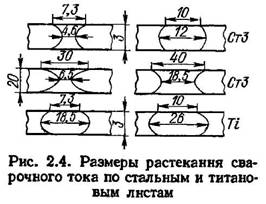
Линии тока сильно сжаты (рис. 2.4). В момент сваривания точки, когда удельное сопротивление металла вокруг ядра возрастает в несколько раз, а магнитная проницаемость становится равной единице, линии тока (рис. 2.4, правая часть) растекаются до размера b = 12 мм.

Произведя расчет по тем же формулам для сварки листов большой толщины δ + δ = 20 +20 мм при d_т = 40 мм, I = 60 кА, Р = 100 кН, D = 100 мм, получим d_о = 30 мм, b_о = 6,5 мм, b = 18,5 мм. Как видно, при больших толщинах стали СтЗ растекания тока до конца сварки нет вообще, а в металле он сжимается.

Для немагнитного титана, обладающего высоким удельным сопротивлением и в холодном, и в горячем состоянии, в течение всего процесса сварки наблюдается растекание тока (рис. 2.4, низ).

В условиях производства никаких расчетов картин растекания или концентрации тока не производят. Рассмотренные здесь примеры имеют цель дать представление об очень сложной электротепловой динамике, которая имеет место не только по плоскости контакта, но и по толщине металла. Многие расчетные формулы часто имеют большое познавательное значение, показывая, от каких именно переменных величин и в какой их связи зависят электрические, тепловые и другие процессы при контактной сварке.