РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ

РАСТЯЖЕНИЕ-СЖАТИЕ

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.1, 2.2), гл. 3 (§ 3.1, 3.4, 3.6–3.12).

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 2.

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 1 (§ 1.3), гл. 2.

Основные понятия и формулы

Растяжение-сжатие – простейший вид деформации стержня. При растяжении-сжатии в стержне из шести видов внутренних усилий возникает только одно усилие – продольная сила N.

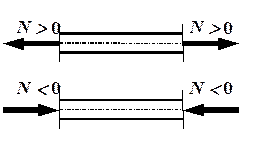Рис.1.1. Правило знаков для продольной силы

Для определения внутренних усилий в стержнях и стержневых системах используется метод сечений. Согласно этому методу продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 1.1). Часто внутреннее усилие меняется по длине стержня, в этом случае принято рисовать график изменения усилия вдоль оси стержня, который называется эпюрой. Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти 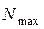при растяжении-сжатии). Сечение, где действует максимальное усилие, будем называть опасным.

После определения продольной силы можно найти нормальное напряжение в поперечном сечении стержня при растяжении-сжатии по формуле

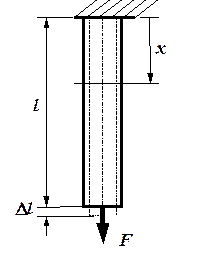Рис. 1.2. Деформация растянутого стержня

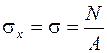. (1.1)

Абсолютная деформация стержня (его удлинение или укорочение) в том случае, если материал стержня работает упруго, т. е. подчиняется закону Гука, определяется так:

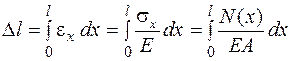(1.2)

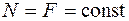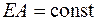На рис. 1.2 показано удлинение стержня Dl, загруженного силой F.Если не учитывать собственный вес, то продольная сила не меняется по длине стержня (для стержня, показанного на рис. 1.2, ) и , то

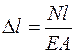. (1.3)

Если задача решается с учетом собственного веса, т. е. усилие N линейно зависит от х, то из (1.2) при 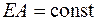можно получить формулу

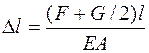, (1.4)

где 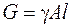– собственный вес стержня; g – объемный вес материала.

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ