Влияние вертикальной рефракции на точность тригонометрического нивелирования

Нивелирование является одним из главнейших видов геодезических работ. Первые сведения о водяном нивелире связывают с именами римского архитектора Марка Витрувия (1 в. до н.э.) и древнегреческого учёного Герона Александрийского (1 в. н.э.). Дальнейшее развитие методов нивелирования связано с изобретением зрительной трубы (конец 16 в.), барометра (Э. Торричелли, 1648), сетки нитей в зрительных трубах (Ж. Пикар, 1669), цилиндрического уровня (английский оптик Дж. Рамсден, 1768).

В 18 веке высоты пунктов в России определяли барометром. Тригонометрическое нивелирование стали применять в начале 19 века. В 1836-37гг. под руководством В.Я. Струве тригонометрическим нивелированием были определены разности уровней Каспийского и Чёрного морей и высоты гор Бештау, Казбек и Эльбрус.

Под тригонометрическим (геодезическим) нивелированием понимается определение разности высот точек местности по измеренному углу наклона направления с одного пункта на другой и известному (или измеренному) горизонтальному расстоянию между этими пунктами.

Тригонометрическое нивелирование применяется для определения высот пунктов триангуляции и полигонометрии, а также при топографических съёмках. Точность его результатов в основном зависит от трудно учитываемого влияния земной рефракции.

По принципу Ферма, световой луч проходит от точки к точке по такому пути, на который затрачивается наименьшее время. Вследствие неравномерной плотности атмосферы световой луч имеет в ней не прямолинейную, а изогнутую форму и обращён своей выпуклостью в сторону менее плотных воздушных масс. При выполнении тригонометрического нивелирования наблюдатель в некоторой точке А (рис.2.19) видит точку В не по прямой АВ, а по направлению последнего элемента визирного луча, т.е. по направлению касательной AD к визирному лучу ВсА в точке А. Проекция угла DAB на вертикальную в точке А плоскость, проходящую через точку В, называется углом вертикальной рефракции.

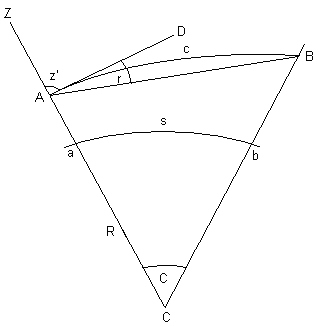
Рис.2.19. Вертикальная рефракция в тригонометрическом нивелировании

Вертикальная рефракция возрастает с увеличением расстояния между пунктами и, кроме того, зависит от времени дня, облачности, высоты луча над Землёй, характера земного покрова и т.д. Поэтому точный учёт вертикальной рефракции невозможен, а вертикальные углы в триангуляции измеряются обычно с несколько меньшей точностью, чем горизонтальные.

На рис.2.19 пусть А – центр прибора в пункте наблюдения; В – верх визирной цели; АсВ – рефракционная кривая (проекция визирного луча на вертикальную в пункте А плоскость, проходящую через В); ZC – направление отвесной линии в пункте А; z¢ - измеренное зенитное расстояние; r – угол вертикальной рефракции; z¢+ r = z – истинное зенитное расстояние; а – пересечение отвесной линии с уровенной поверхностью, от которой ведётся счёт высот; ав – пересечение вертикальной в пункте А плоскости с исходной уровенной поверхностью. Дугу ав примем за дугу окружности радиуса R, равного среднему радиусу кривизны земного эллипсоида на широте пункта А.

По построению отрезок Аа=Н₁ есть высота пункта А. Отрезок Вв может отличаться от высоты пункта В по причине того, что форма уровенной поверхности может отличаться от сферической. Пренебрегая этим, примем Вв=Н₂. Горизонтальное расстояние между пунктами А и В примем равным длине дуги ав=s.

В геодезии доказывается

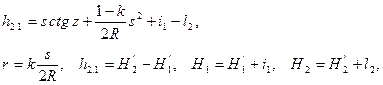(2.26)

где k – коэффициент рефракции, равный в среднем 0,14;

H¢_i (i=1, 2) – высоты центров пунктов А и В соответственно;

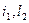– высоты прибора и знака над центрами пунктов А и В соответственно.

Член 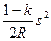обусловлен влиянием сферичности Земли и рефракции и называется поправкой за кривизну Земли и рефракцию.

Существуют различные способы тригонометрического нивелирования (одностороннее, двухстороннее, способ створов), что вызвано стремлением ослабить влияние земной рефракции. Рассматриваются две гипотезы действия земной рефракции на результаты измерения вертикальных углов (зенитных расстояний). В первой предполагается равенство углов земной рефракции при измерении вертикальных углов на концах линии в направлении друг друга. Другая гипотеза предполагает равенство углов земной рефракции при одновременных измерениях вертикальных углов с точки стояния прибора в любых направлениях. Первая гипотеза учитывает разнообразие условий рельефа по линиям, вторая – идентичность условий наблюдений в пункте стояния приборов.

Сложившаяся практика выполнения тригонометрического нивелирования основана на использовании одностороннего и двухстороннего способов с использованием горизонтальных проложений. Способы с непосредственно измеренными наклонными расстояниями не применяются.

Для определения коэффициента рефракции применяют следующие способы:

• по измеренному углу между двумя точками, разность высот и расстояние между которыми известны с достаточной точностью;
• по одновременным взаимным измерениям углов наклона;
• определением поправки к принятому значению коэффициента по данным тригонометрического нивелирования.

В первом способе высоты точек определяются геометрическим нивелированием, а расстояния либо известны из триангуляции, либо измеряются дальномерами. Из (2.26) следует

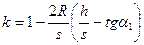, (2.27)

где 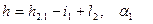- угол наклона, измеренный в пункте А.

Пусть 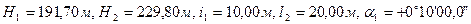. Тогда 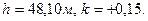Вычислим среднюю квадратическую ошибку определения коэффициента рефракции этим способом.Пренебрегая ошибками определения h и s, запишем

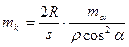. (2.28)

При малых углах a

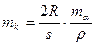. (2.29)

Из (2.29) следует, что при измерении углов наклона с равной точностью коэффициент рефракции определяется тем точнее, чем больше расстояние. Оценим, с какой точностью следует измерять углы наклона. Средняя квадратическая ошибка

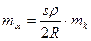(2.30)

при 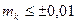и s = 10км 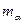будет равна ±1,6².

Во втором способе принимается, что для взаимных направлений прямого и обратного коэффициенты 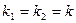и поэтому определяется только один коэффициент. Формула для вычисления коэффициента рефракции имеет вид

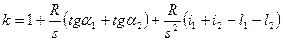. (2.31)

С достаточной точностью для практики запишем

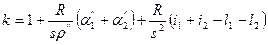. (2.32)

Примем, что углы наклона измеряются равноточно, расстояние и высоты знаков и приборов определены с пренебрегаемо малыми ошибками. Тогда

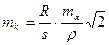. (2.33)

В практике тригонометрического нивелирования прямое и обратное направления обычно наблюдаются неодновременно. К тому же принимаемое равенство коэффициентов рефракции для взаимных направлений не соответствует действительности. Поэтому результаты определения коэффициента рефракции первым и вторым способами нельзя сравнивать между собой.

В третьем способе принимают

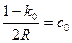, (2.34)

где 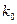- принятое для обработки тригонометрического нивелирования значение коэффициента рефракции.

Затем находят поправку к коэффициенту с₀ под условием, что прямое и обратное превышения, вычисленные со значением с₀+Dс₀, равны между собой по абсолютной величине и противоположны по знаку. Поправку вычисляют по формуле

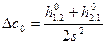, (2.35)

где

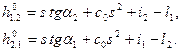(2.36)

Средняя квадратическая ошибка определения поправки вычисляется по формуле

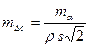. (2.37)

Исправление принятого коэффициента рефракции не изменит средних значений из прямого и обратного превышений по каждой стороне. Но оно исключит систематическую часть расхождений между ними. Исправление коэффициента рефракции изменит превышения, полученные из односторонних наблюдений. Повышение точности определения высот пунктов, определяемых из односторонних наблюдений, является основным назначением исправления принятого коэффициента рефракции.

В табл. 15 представлены результаты оценки точности определения разности высот пунктов, определённых односторонним тригонометрическим нивелированием. Вычисления выполнены по формуле

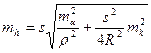, (2.38)

которую легко получить из (2.26), пренебрегая ошибками определения расстояния, высот прибора и визирной цели.

Таблица 15

S, км
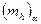
	0,04	0,06	0,09	0,12	0,15	0,29	0,44
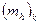
	0,02	0,04	0,08	0,15	0,23	0,94	2,12
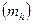
	0,05	0,07	0,12	0,19	0,28	0,99	2,16

Из табл.15 видно, что для больших сторон влияние ошибки определения коэффициента рефракции является преобладающим.

В триангуляции обычно применяется двухстороннее нивелирование, выполняемое в разное время. Исследования показали, что на точность нивелирования оказывают влияние не только возмущения рефракционного поля в месте наблюдения, но также в промежуточных областях и в месте расположения наблюдаемого пункта. Для правильной постановки тригонометрического нивелирования важно знать причины изменения коэффициента рефракции и возмущений рефракционного поля.

Теоретические исследования и производственный опыт показывают, что основной причиной изменений коэффициента рефракции являются изменения вертикального градиента температуры в приземных слоях атмосферы. Известна формула

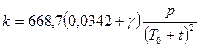, (2.39)

где g - вертикальный градиент температуры, т.е. мера изменения температуры воздуха с увеличением высоты на выбранную единицу длины. В (2.39) он выражен в градус/метр (градус на метр);

р – атмосферное давление, выраженное в миллиметрах ртутного столба;

T₀ = 273° и t – температура воздуха по стоградусной шкале Цельсия.

Для нормального адиабатического состояния приземного слоя воздуха градиент g ₀ = - 0,0098 град/м и в этом случае формула (2.39) принимает вид

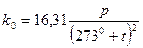. (2.40)

Вычисленный по (2.40) коэффициент называется нормальным адиабатическим коэффициентом рефракции.

Стандартный температурный градиент g _с = - 0,0065 град/м. С этим значением температурного градиента вычисляется нормальный стандартный коэффициент рефракции по формуле

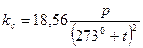. (2.41)

Распределение температуры в нижних слоях воздуха определяется главным образом теплообменом между почвой и воздухом. При равных условиях градиенты температуры больше в засушливых районах, чем во влажных. Над растительными покровами (лес, луг) градиенты температуры меньше, чем над оголённой почвой.

В дневное время и в ясную погоду температурный градиент вблизи земной поверхности (до высоты 1-1,5м над почвой) может достигать больших значений, что ведёт к уменьшению коэффициента рефракции. На высоте нескольких десятков метров градиент температуры становится близким к нормальному. Вечером наступает охлаждение почвы и приземных слоёв воздуха. В этих слоях температура начинает не убывать с высотой, а возрастать, конвекционный теплообмен затухает. Такое изменение в распределении температуры, когда она снизу вверх не убывает, а возрастает, называется инверсией температуры. В период инверсии коэффициент рефракции претерпевает значительные изменения.

Периоды возникновения и исчезновения инверсии наступают тогда, когда Солнце находится на высоте около 15° над горизонтом. На этой высоте Солнце бывает в летнее время примерно за 3 часа до захода и через 3 часа после восхода. Этот период отсутствия инверсии (в летнее время в средних широтах с 9 до 17 часов) рекомендуется для измерения вертикальных углов. В пасмурную погоду колебания градиентов температуры происходят значительно медленнее, период благоприятного времени для измерения вертикальных углов увеличивается, однако в пасмурную погоду не следует измерять вертикальные углы ранним утром и поздним вечером. Зимнее время непригодно для тригонометрического нивелирования, так как температурные градиенты соответствуют инверсии температуры, при этом сильно возрастают случайные колебания коэффициента рефракции.

Геодезистами уже давно замечена связь изменения коэффициента рефракции с колебаниями изображений наблюдаемых предметов. Это явление ещё в середине 19 века академик В.Я.Струве объяснял так: «Причину этого изменения надо искать во влиянии большего или меньшего нагрева земной поверхности (почвы), что нарушает правильную слоистость воздуха. Если почва теплее, чем соприкасающийся с ней воздух, то происходит расширение нижних слоёв воздуха, которое приводит к уменьшению рефракции и, благодаря поднятию тёплого воздуха, к колебаниям изображений. Если температура почвы равна температуре воздуха, то имеет место правильная слоистость воздуха, изображения успокаиваются, и этому состоянию соответствует нормальная рефракция».

В вопросах рефракционных влияний важна высота прохождения визирного луча над подстилающей поверхностью. Из–за различий подстилающей поверхности визирный луч будет проходить через области с разными температурными градиентами. По этой причине не рекомендуется передавать высоты тригонометрическим нивелированием, если высота визирного луча составляет менее 1,5м над земной поверхностью.

Целесообразно также приёмы измерения вертикальных углов разделять промежутками времени (0,5-1ч), для того чтобы приблизить измерения к некоторым средним условиям дня. Рекомендуется половину приёмов выполнять до полудня, а другую после полудня. При таком распределении наблюдений по времени будет достигаться их симметричность относительно изменения градиентов температуры. Такая методика призвана компенсировать в известной мере ошибки, происходящие из-за изменений коэффициента рефракции.

При правильной постановке тригонометрического нивелирования и строгой математической обработке его данных и при условии, что некоторые геодезические пункты являются и астрономическими, можно получить обширный материал для изучения фигуры Земли (определить высоты физической поверхности над земным эллипсоидом и составляющие уклонения отвесных линий). При этом могут быть испытаны гипотезы о вертикальной составляющей рефракции и оценена её величина на каждом пункте.

До сих пор, к сожалению, к измерению зенитных расстояний предъявляются пониженные требования. Так, при конструировании и изготовлении теодолитов вертикальные круги делают менее точными, чем горизонтальные, понижены требования к изготовлению уровня при алидаде вертикального круга. Зенитные расстояния измеряются в одной и той же части вертикального круга. Современная практика требует уточнения основных положений методики выполнения тригонометрического нивелирования и повышения требований к изготовлению новых угломерных приборов.

ЛИТЕРАТУРА

1. Атлас офицера. М., РИО ВТУ ГШ, 1984.

2. Е.П. Аксенов. Теория движения искусственных спутников Земли. М., Наука, 1977.

3. С.В. Зверева.В мире солнечного света. Л., Гидрометеоиздат, 1988.

4. Б.С. Кузьмин, Б.А. Литвинов. Руководство по геодезии (Общие сведения и триангуляция). М., ВИА, 1961.

5. Н.В. Короновский.Общая геология. М., изд-во Московского университета, 2002.

6. Г.Д. Курошев.Геодезия и география. СПб., изд-во СПб университета, 1999.

7. Курс астрономии (часть теоретическая) Н. Цингера. Петроград, РИО Морского комиссариата, 1922.

8. М.М. Машимов. Планетарные теории геодезии. М., Недра, 1982.

9. М.М. Машимов. Высшая геодезия. Методы изучения фигуры Земли и создания общеземной системы геодезических координат. М., ВИА, 1991

10. М.М. Машимов. Геодезические этюды. Журнал «Геодезия и картография» №1, 2. М., Картгеоцентр-Геодезиздат, 1996.

11. П. Мельхиор.Физика и динамика планет. Пер. с франц. Части 1, 2. М., Мир, 1975.

12. Г. Мориц.Современная физическая геодезия. Пер. с англ. М., Недра, 1983.

13. Справочник геодезиста. Книги 1, 2. М., Недра, 1985.

14. В. Торге.Гравиметрия. Пер. с англ. М., Мир, 1999.

15. Физика космоса.Маленькая энциклопедия. М., Советская энциклопедия, 1976.