Основные закономерности фильтрования

Ввиду небольшого размера отверстий в слое осадка и фильтровальной перегородке, а также малой скорости движения жидкой фазы в них можно считать, что фильтрование протекает в ламинарной области. При этом условии скорость фильтрования в каждый данный момент прямо пропорциональна разности давлений и обратно пропорциональна вязкости жидкости фазы и общему гидравлическому сопротивлению слоя осадка и фильтровальной перегородки. В связи с тем, что в общем случае в процессе фильтрования значения разности давлений и гидравлического сопротивления слоя осадка с течением времени изменяются, то переменную скорость фильтрования w (м/сек) выражают в дифференциальной форме, а основное уравнение фильтрования имеет вид:

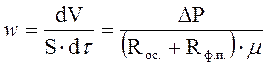, (2-86)

где V- объем фильтрата, м³; S - поверхность фильтрования, м²; t - продолжительность фильтрования, сек; DR - разность давлений, Н/м²; m - вязкость жидкой фазы суспензии, Н×сек/м²; R_oc - сопротивление слоя осадка, м^-1; R_ф.п. - сопротивление фильтровальной перегородки (его можно считать приблизительно постоянным).

Величина R_ос по мере увеличения толщины слоя осадка изменяется от нуля в начале фильтрования до максимального значения в конце процесса. Для интегрирования уравнения (2-86) необходимо установить зависимость между R_оси объемом полученного фильтрата. Учитывая пропорциональность объемов осадка и фильтрата, обозначим отношение объема осадка V_ос к объему фильтрата V через х₀.Тогда объем осадка V_ос = х₀×v. Вместе с тем объем осадка может быть выражен как V_ос = h_oc×S, где h_oc – высота слоя осадка. Следовательно:

V×x_o=h_oc×S.

Отсюда толщина равномерного слоя осадка на фильтровальной перегородке составит:

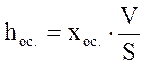, (2-87)

а его сопротивление

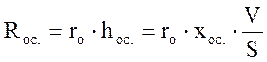, (2-88)

где r_o - удельное сопротивление слоя осадка, м^-2.

Подставив значение R_oc из выражения (2-88) в уравнение (2-86) получим:

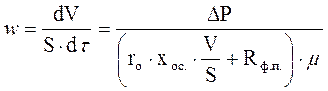. (2-89)