Осаждение в гравитационном поле (отстаивание)

Скорость осаждения в гравитационном поле невелика. Поэтому процесс отстаивания малоэффективен и не обеспечивает выделения из разделяемой системы частиц с высокой степенью дисперсности.

Рассмотрим процесс падения частицы в вязкой среде и выведем уравнение для определения скорости отстаивания. На рис.2.45. схематически представлены силы, действующие на падающую частицу шарообразной формы диаметром "d".

Для частицы с диаметром "d" и плотностью «r_ч» сила тяжести, составляет:

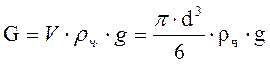, (2-75)

где V - объем частицы; g - ускорение свободного падения.

Согласно закону Архимеда, подъемная сила:

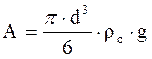, (2-76)

где r_c - плотность среды, в которой находится частица.

Сила, заставляющая частицу падать:

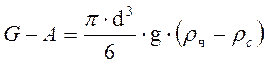(2-77)

Среда, в которой падает частица, оказывает сопротивление R, которое будет зависеть от ее вязкости и плотности r_c , площади сечения частицы F и ее формы. Величина силы R определяется по закону Ньютона

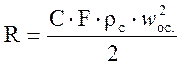, (2-78)

где С - коэффициент сопротивления среды, зависящий от режима движения частицы; w_oc - скорость осаждения частицы.

Осаждающаяся частица в начале своего движения движется ускоренно. Однако участок такого движения невелик. Т.к. сила (G-А) становится равной силе R , то в дальнейшем частица начинает двигаться равномерно со скоростью w_oc. Значение w_oc может быть найдено из условия (G-А)=R. Приравнивая уравнения (2-77) и (2-78 и преобразуя их (обе части умножим на 1/n²) получим уравнение осаждения:

,

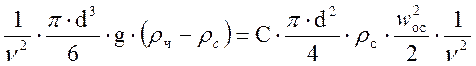или в критериальном виде:

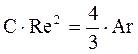, (2-79)

где 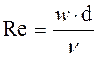; 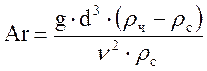(критерий Архимеда).

При осаждении крупных частиц (размер больше 0,1мм) в относительно маловязкой среде основное сопротивление вызывается силами инерции, под действием которых происходит отрыв струй и образование турбулентных вихрей за опускающейся частицей, а силы трения играют второстепенную роль.

В условиях турбулентного режима (Re ³ 500) сопротивление среды пропорционально квадрату скорости и коэффициенту сопротивления С=0,44. Тогда:

Re² = 3,03Ar. (2-80)

Отсюда:

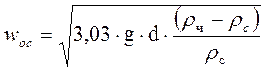. (2-81)

При ламинарном режиме Re 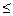2 сопротивление среды пропорционально первой степени и 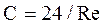. Подставляя это значение "С" в уравнение (2-79), получим

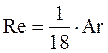. (2-82)

Тогда:

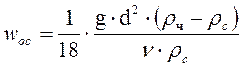. (2-83)

Выражение (2-83) носит название формулы Стокса.

В суспензии и эмульсии обычно имеются частицы разных размеров. Расчет необходимо вести для частиц меньшего размера, т.к. если создать условия для осаждения мелких частиц, то для крупных они будут заведомо достаточны. Из уравнения (2-83) видно, что скорость осаждения возрастает с увеличением диаметра частиц, разности плотностей осаждаемых частиц и среды, и понижением ее вязкости. Поэтому для более эффективного проведения процесса отстаивания необходимо воздействовать теми или иными способами именно на эти параметры. Так, уменьшая вязкость и плотность среды путем повышения ее температуры или разбавления маловязким растворителем, можно увеличить скорость осаждения. Соответствующее воздействие на размеры осаждаемых частиц с целью их увеличения (добавление коагулянтов; электрического поля высокого напряжения) приводит к значительному повышению скорости осаждения.

Для определения расчетной скорости движения w_p необходимо учесть влияние формы частиц и объемной концентрации суспензии путем введения коэффициентов j и l. Тогда расчетная скорость:

w_p = w_oc×j×l,

где С_v – объемная концентрация (в долях):

j = 0,43…0,77, l = .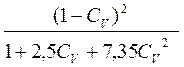

Расчет отстойников

В прямоугольный отстойник (Рис.2.46.) с размерами l, h, b поступает на разделение неоднородная смесь с линейной скоростью v. Рабочий объем отстойника равен V= l×h×b=V_t×t₀ , где V_t - секундная производительность отстойника, м3/с; t₀ - средняя продолжительность отстаивания частиц, с. t₀, выраженная через среднюю скорость отстаивания частиц ×v₀, равна: t₀= h/×v₀.

Удельная производительность отстойника:

V_t = l×b×v₀ , (2-84)

т.е. она равна произведению площади отстаивания F₀= l×b на скорость отстаивания.

Если задана производительность отстойника, то из уравнения (2-84) можно определить площадь поверхности отстаивания:

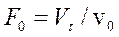. (2-85)

Уравнение (2-84) показывает, что производительность отстойника зависит только от скорости и поверхности осаждения, а не от его высоты. Поэтому отстойники имеют значительную площадь при небольшой высоте, которая обычно не превышает 1,8-4,5 м, а для отстойников очень больших диаметров не более 7 м. Это условие реализовано, например, в конструкциях многоярусных отстойников.