Понятие о квантовой статистике Бозе — Эйнштейна

И Ферми- — Дирака

Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невзаимодействующих частиц задается с помощью так называемых чисел заполнения N — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами системы, состоящей из многих тождественных частиц.

Для систем частиц, образованных бозонами — частицами с нулевым или целым спином), числа заполнения могут принимать любые целые значения: 0, 1, 2, ... . Для систем частиц, образованных фермионами — частицами с полуцелым спином, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых . Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения .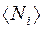

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна . Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:

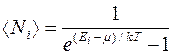(4.2.1)

Это распределение называется распределением Бозе — Эйнштейна. Здесь 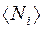— среднее число бозонов в квантовом состоянии с энергией E_i, k — постоянная Больцмана, Т — термодинамическая температура, 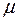— химический потенциал; 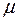не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех 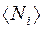равна полному числу частиц в системе. Здесь 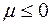, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.

Идеальный газ из фермионов — ферми-газ —описывается квантовой статистикой Ферми — Дирака . Распределение фермионов по энергиям имеет вид

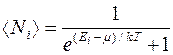, (4.2.2)

где 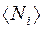— среднее число фермионов в квантовом состоянии с энергией 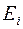, 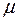— химический потенциал. В отличие от (4.2.1) 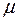может иметь положительное значение (это не приводит к отрицательным значениям чисел 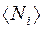). Это распределение называется распределением Ферми — Дирака.

Если 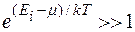, то распределения Бозе — Эйнштейна (4.2.1) и Ферми — Дирака (4.2.2) переходят в классическое распределение Максвелла — Больцмана:

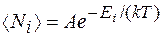(4.2.3)

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчи-няющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низких температурах и больших плотностях. Параметром вырождения называется величина А. При A <<1, т.е. при малой степени вырождения, распределения Бозе — Эйнштейна (4.2.1) и Ферми — Дирака (4.2.2) переходят в классическое распределение Максвелла — Больцмана .

Температурой вырождения 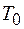называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т.е. 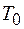— температура, при которой вырождение становится существенным. Если 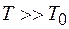, то поведение системы частиц (газа) описывается классическими законами.