Математические модели пассивных компонентов

Резистор

Математическая модель резистора (рис. 2.1) описывается законом Ома:

U_R=I×R, или I=g×U_R, где g=1/R.

В первом случае задано падение напряжения U_R на резисторе, а искомая величина – ток I через резистор. Во втором случае задан ток Iчерезрезистор, а искомая величина – это U_R на резисторе.

Параметры математической модели:

· номинальное значение сопротивления R_Н;

· допуск на сопротивление dR;

· температурный коэффициент ТКR.

Допуск dR является границей отклонений сопротивления от номинального значения, возникающих в процессе изготовления резисторов:

при этом сопротивления резисторов в процессе их производства могут принимать значения:

Если значение сопротивления R меньше номинального R_H , то относительное отклонение DR/ R_H < 0, в противном случае DR/ R_H > 0.

Обычно допуск dR задается в процентах.

Температурный коэффициент ТКR задает значение сопротивления для текущего значения температуры Т:

,

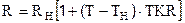где Т_Н – номинальное значение температуры, принимаемое равным 27⁰ С.

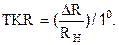
Таким образом, TKRравен относительному отклонению сопротивления от номинального значения при изменении температуры на 1⁰ С. Иногда TKR задается в propromil (ppm):

TKR_ppm= TKR × 10⁶.

Конденсатор

Математическая модель конденсатора (рис. 2.2) записывается в виде:

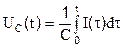или

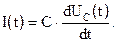
В первом случае заданной величиной является падение напряжения U_C(t) на конденсаторе, а искомой – ток через конденсатор I(t). Во втором случае заданной величиной является ток через конденсатор I(t), а искомой – падение напряжения U_C(t).

Параметры математической модели:

· номинальное значение емкости C_H;

· допуск на емкость dС;

· температурный коэффициент TKC.

Понятие о допуске и температурном коэффициенте были даны при описании модели резистора.