ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ

Для расчета плотности теплового потокаq при теплопередаче через однослойную плоскую стенкунеобходимо знатьтолщину стенки δ, ко-эффициент теплопроводности стенки λ, температуры теплоносителей Т₁ и Т₂ ,коэффициенты теплообмена с обеих сторон стенки α₁ и α₂ (рис. 5.1).

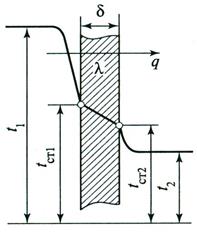
Рис. 5.1. Схема теплопередачи через

однослойную плоскую стенку

При стационарном режиме теплообмена плотности теплового потока от первого теплоносителя к стенке, через стенку и от стенки ко второму теплоносителю одинаковы, т.е.

q = α₁(Т_ж1 – Т_ст1) = λ(Т_ст1 – Т_ст2)/δ = α₂(Т_cт2 – Т_ж2) (5.3)

или Т_ж1 – Т_ст1 = q/α₁; Т_ст1 – Т_ст2 = qδ /λ; Т_cт2 – Т_ж2 = q/α₂. (5.4)

Просуммировав уравнения (5.4), получим:

q = (Т_ж1 – Т_ж2) /(1/α₁ + δ /λ +1/α₂) = k(Т_ж1 – Т_ж2). (5.5)

Следовательно, значение коэффициента теплопередачи

k = 1/(1/α₁ + δ /λ +1/α₂), (5.6)

Значение k всегда меньше наименьшего коэффициента теплоотдачи α.

Отсюда полное термическое сопротивление теплопередачи имеет вид:

R = 1/k = 1/α₁ + δ /λ +1/α₂. (5.7)

Из (5.7) следует, что полное термическое сопротивление теплопередачи равно сумме отдельных, так называемых частных термических сопротивлений: термического сопротивления теплоотдачи (1/α₁) со стороны теплоносителя с более высокой температурой; термического сопротивления теплопроводности стенки (δ /λ); термического сопротивления теплоотдачи (1/α₂) со стороны теплоносителя с более низкой температурой.

Неизвестные температуры стенок Т_ст1 и Т_ст2 можно определить из уравнений (5.4):

Т_ст1 = Т_ж1 – q/α₁;

(5.8)

Т_ст2 = Т_ж2 + q/α₂.

Если стенка состоит изn слоевтолщиной δ₁, δ₂, ..., δ_n, коэф-фициенты теплопроводности которых λ₁, λ₂, ..., λ_n, то с помощью аналогичных выкладок получим следующее выражение для коэф-фициента теплопередачи:

_n

k = 1/(1/α₁ + ∑δ_i/λ_i +1/α₂), (5.9)

^{i = 1}

а полное термическое сопротивление теплопередаче через многослойной плоскую стенку

_n

R = 1/α₁ + ∑δ_i/λ_i +1/α₂. (5.10)

^{i = 1}

ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ

СТЕНКУ

Для получения расчетной формулы плотности теплового потокаq при теплопередаче через однослойную цилиндрическую стенкунеоб-ходимо знатьнаружный d₂ и внутренний d₁ диаметр цилиндра, коэффи-циент теплопроводности стенки цилиндра λ, температуры теплоносите-лей Т₁ и Т₂ ,коэффициенты теплообмена с обеих сторон стенки α₁ и α₂ (рис. 5.2).

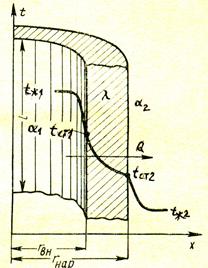
Рис. 5.2. Схема теплопередачи через однослойную

цилиндрическую стенку

При стационарном режиме теплообмена плотности теплового по-тока, приходящиеся на каждый метр длины цилиндрической стенки, от первого теплоносителя к стенке, через стенку и от стенки ко второму теплоносителю одинаковы. С учетом формулы (2.41) тепловые потоки, приходящиеся на единицу длины цилиндрической стенки, можно выразить уравнениями:

q_l = Q/ℓ =α₁πd₁(Т_ж1–Т_ст1); (5.11)

q_l = π(Т_ст1–Т_ст2)/(1/ 2λ) ln(d₂/d₁); (5.12)

q_l =α₂πd₂(Т_ст2–Т_ж2). (5.13)

Определим из уравнений (5.11)-(5.13) разности температур в явном виде:

Т_ж1–Т_ст1 = q_l/α₁πd₁; (5.14)

Т_ст1–Т_ст2 = q_l ln (d₂/d₁)/2πλ; (5.15)

Т_ст2–Т_ж2 = q_l /α₁πd₁. (5.16)

Просуммировав правые и левые части равенств (5.14)-(5.16), получим для теплового потока q_l следующую формулу:

q_l = π(Т_ж1–Т_ж2) / [1/α₁d₁ +ln (d₂/d₁) /2λ +1/α₂d₂] = k_l π(Т_ж1–Т_ж2), (5.17)

откуда получим выражение для линейного коэффициента теплопередачи, который определяет тепловой поток, приходящийся на единицу длины цилиндрической стенки:

k_l = 1/ [1/α₁d₁ + ln (d₂/d₁)/2λ + 1/α₂d₂]. (5.18)

Линейный коэффициент теплопередачи имеет размерность Вт/(м·К).

Из уравнений (5.13)-(5.15) получим выражения для определения неизвестных температур Т_ст1 и Т_ст2 :

Т_ст1 = Т_ж1 - q_l /α₁πd₁;

(5.19)

Т_ст2 = Т_ж2 + q_l /α₂πd₂.

Если цилиндрическая стенка состоит изn слоеви заданы (известны) диаметры каждого слоя, коэффициенты теплопроводности каждого слоя, температуры теплоносителей и коэффициенты теплообмена с обе-их сторон многослойной стенки, то линейный коэффициент теплопе-редачи определяется по формуле:

_n

k_l = 1/ [1/α₁d₁ + ∑ (1/2λ_i) ln (d_{i + 1}/d_i) +1/α₂d_{n +1}]. (5.20)

^{i = 1}

Температура поверхностей, соприкасающихся с теплоносителем, определяется из формул, аналогичных уравнениям (5.18):

Т_ст1 = Т_ж1 - q_l /α₁πd₁;

(5.21)

Т_{ст n+1} = Т_ж2 + q_l /α₂πd_n+1.