КРИТИЧЕСКАЯ ТОЛЩИНА ТЕПЛОВОЙ ИЗОЛЯЦИИ

Для снижения потерь тепла в окружающую среду необходимо увеличение полного термического сопротивления нагретого тела. Чаще всего это достигается путем нанесения на нагретую поверхность слоя тепловой изоляции. Для тепловой изоляции могут быть использованы материалы с низким коэффициентом теплопроводности [λ ≤ 2 Вт/(м·К)] и достаточно стабильными другими физическими характеристиками - асбест, слюда, пенопласты, шлаковая или стеклянная вата и др.

Анализ формулы полного термического сопротивления плоской стенки (5.10) показывает, что слой тепловой изоляции любой толщины независимо от величины ее коэффициента теплопроводности приводит к увеличению полного термического сопротивления стенки и уменьшению тепловых потерь; чем толще слой изоляции, тем меньше тепловые потери..

Это правило не может быть распространено на тела, имеющие вы-пуклые поверхности, например, на трубы . При наложении изоляции на выпуклую поверхность внутреннее термическое сопротивление увеличивается, но из-за увеличения поверхности соприкосновения стенки (наружной поверхности изоляции) с внешним теплоносителем уменьшается внешнее термическое сопротивление. Поэтому при использовании материалов с достаточно большим коэффициентом теплопроводности для покрытия изоляцией выпуклой поверхности можно получить не уменьшение, а увеличение теплового потока, т.е. тепловые потери могут увеличиться. Следовательно, необходимо исследовать на экстремум зависимость полного термического сопро-тивления теплопередаче многослойной цилиндрической стенки от на-ружного диаметра тепловой изоляции.

Установим условие, при котором материал, используемый для изоляции трубы, уменьшает тепловой поток . Для однородной трубы, покрытой слоем изоляции (рис. 5.3), из формулы (5.20) получим:

1/k_l = 1/α₁d₁ + (1/2λ) ln (d₂/d₁)+ (1/2λ_из) ln (d_из/d₂) + 1/α₂d_из, (5.22)

где k_l – линейный коэффициент теплопередачи.

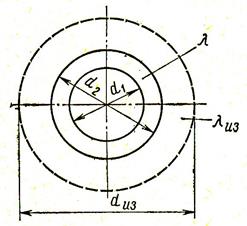
Рис. 5.3. Влияние тепловой изоляции на коэффициент теплопередачи

Анализ уравнения общего термического сопротивления двухслойной цилиндрической стенки (5.22) показывает, что при увеличении внешнего диаметра изоляции d_из увеличивается сопротивление слоя изоляции [член (1/2λ_из) ln (d_из/d₂)], но одновременно уменьшается сопротивление теплоотдачи на наружной поверхности изоляции (член 1/α₂d_из). Выявим экстремум функции 1/k_l = f (d_из) в предположении, что коэффициент теплоотдачи α₂ не зависит от наружного диаметра изоляции d_из.

Приравняем нулю первую производную полного термического сопротивления теплопередаче по наружному диаметру изоляции:

(1/k_l)' = 1/(2λ_изd_из) - 1/(α₂d²_из) = 0. (5.23)

Отсюда критический диаметр изоляции, отвечающий экстремуму, оп-ределяется формулой:

d_кр =2λ_из/α₂. (5.24)

Из уранения (5.24) следует, что критический диаметр изоляции не зависит от тощины слоя изоляции, от коэффициента теплоотдачи α₁ (от теплоносителя к внутренней поверхности трубы), ни от наружного, ни от внутреннего диаметров трубы. Он будет тем меньше, чем меньше коэффициент теплопроводности изоляции λ_из и чем больше коэффици-ент теплоотдачи α₂ от наружной поверхности изоляции к окружающей среде.

Определим вторую производную полного термического сопротивле-ния теплопередаче по наружному диаметру изоляции:

(1/k_l)" = - 1/(2λ_изd²_из) + 2/(α₂d³_из). (5.25)

Подставив в уравнение (5.25) вместо d_из значение d_кр из (5.24), полу-чим:

(1/k_l)" =α₂²/(8λ³_из) >0. (5.26)

Так как вторая производная (1/k_l)" больше нуля, то критический диаметр соответствует минимуму полного термического сопротивления теплопередаче и максимуму теплового потока (рис. 5.4).

Пригодность тепловой изоляции удобно определять по параметру:

А_кр = d_кр/d₂. (5.27)

С учетом выражения (5.24) для d_кр можно записать:

А_кр = 2λ_из/(α₂d₂) . (5.28)

При А_кр > 1 из формулы (5.27) получается d₂ < d_кр. Как видно из рис. 5.4 в этом случае увеличение диаметра d_из от d₂ до d_кр приведет к уве-личению линейного коэффициента теплопередачи, а значит, к увеличе-нию теплового потока (тепловых потерь). Следовательно, изоляцию необходимо признать непригодной.

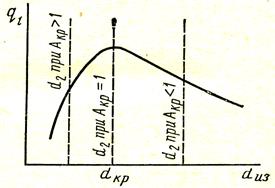
Рис. 5.4. К выбору тепловой изоляции для труб небольшого

диаметра

При А_кр ≤ 1 из формулы (5.27) получается d₂ ≥ d_кр, и потому в соответствии с рис. 5.4 слой изоляции любой толщины позволит уменьшить тепловой поток через стенку трубы.

Таким образом, для того, чтобы изоляция вызвала уменьшение тепловых потерь цилиндрической стенки по сравнению с неизолиро-ванной трубой при заданных наружном диаметре трубы и коэффици-енте теплоотдачи α₂, необходимо, чтобы выполнялось следующее условие:

λ_из ≤α₂d₂/2. (5.29)

Например, при наружном диаметре трубы d₂=40 мм и коэффициенте теплоотдачи внешнего конвективного теплообмена α₂ = 6 Вт/(м²·К) при-годна изоляция с коэффициентом теплопроводности λ_из ≤ 0,12 Вт/(м·К).