Расчет статически неопределимых плоско-пространственных рам методом сил

При расчете пространственных систем, как и при расчете плоских, обычно в целях простоты расчета пренебрегают влиянием на перемещения внутренних сил N_z, Q_x и Q_y, поэтому при расчете пространственных систем чаще всего приходится строить эпюры М_х, М_у и M_z от каждого основного неизвестного и от нагрузки, по которым определяются коэф­фициенты и свободные члены канонических уравнений.

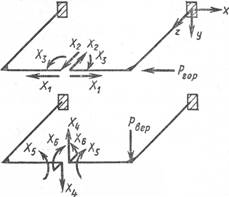Рис. 7

В плоской раме (рис. 7) основные неизвестные Х₁, Х₂, Х₃, лежащие в плоскости рамы, вызывают перемещения только в этой плоскости, поэтому все побочные перемещения от этих сил Х₁, Х₂ и Х₃ по направле­нию остальных основных неизвестных и Х₄, Х₅, Х₆, как и взаимные их перемещения, равны нулю. Следовательно, канонические уравнения для таких систем независимо от нагрузки распадаются на две независимые группы. В одну из них будут входить неизвестные типа Х₁, Х₂ и Х₃, а в другую— неизвестные типа Х_4у Х₅ и Х₆. Если нагрузку также разложить на нагрузку, лежащую в плоскости рамы, и нагрузку, перпендикулярную ей, то нагрузка, лежащая в плоскости рамы, вызывает только основ­ные неизвестные, расположенные в плоскости рамы (Х₁, Х₂ и Х₃), а на­грузка, перпендикулярная плоскости рамы, вызывает неизвестные Х₄, Х₅ и Х₆.

Пример . Построить эпюры изгибающих и крутящих моментов в раме (рис. 8, а), если сечения стержней круглые, E/G = 2,5; Г// = 2.

Основная система показана на рис. 8, б. По условию симметрии будем иметь одно неизвестное Х₁ (изгибающий момент). Эпюры от Х₁=1 показаны на рис. 8, в, а грузовые — на рис. 8, г. Каноническое уравнение:

δ₁₁Х₁ + Δ_1Р = 0.

Коэффициент δ₁₁ и свободный член Δ_1Р при Т = 2I будут:

δ₁₁ = 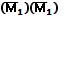= 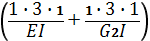2 =

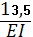
Δ_1Р = = – =– .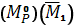

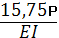Следовательно:

13,5 Х₁ – 15,75Р = 0, откуда Х₁ = 1,167Р.

Окончательные эпюры показаны на рис. 8, д.

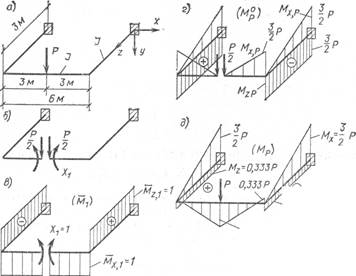
Рис. 8