Общие сведения о пространственных фермах

Пространственные системы подобно плоским в большинстве случаев являются неизменяемыми, поскольку они, как правило, несут различно­го вида нагрузки. Все рассуждения о поведении изменяемых и мгновен­но изменяемых систем при различных нагрузках, а также и соображе­ния об их применении, которые были приведены для плоских систем, принципиально сохраняют свою силу и для систем пространственных. Всякую неизменяемую пространственную систему будем называть те­лом. Каждое свободное тело по отношению к другому имеет шесть сте­пеней свободы, т. е. может совершать три поступательных перемещения и три поворота. Соединение отдельных тел в одно неизменяемое тело производится при помощи связей. Каждая связь имеет кинематическую и статическую характеристики. Кинематические характеристики связей будем рассматривать при бесконечно малых перемещениях.

Различают следующие виды связей пространственных систем.

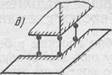
Стержень с шаровыми щарнирами по концам, допускающим пово­роты в любом направлении (плоско-подвижная шаровая связь — рис. 2, а). Кинематическая характеристика: связь уничтожает поступа­тельное перемещение присоединяемого тела вдоль стержня (по оси у), т. е. уничтожает одну степень свободы, но допускает поступательное пе­ремещение присоединяемого тела в плоскости, перпендикулярной стержню (две степени свободы), и повороты вокруг трех осей, проходя­щих, например, через шаровой шарнир (три степени свободы). Статиче­ская характеристика: в связи может возникать реактивная сила вдоль стержня. Стержень с шаровыми шарнирами по концам является основ­ным элементарным видом связи пространственных систем. Связи ос­тальных видов обычно являются различной комбинацией нескольких таких стержней.

Два стержня с общим шаровым шарниром на одном из их концов (линейно-подвижная шаровая связь — рис. 2, б). Кинематическая характеристика: связь уничтожает поступательные перемещения в плос­кости двух стержней (в плоскости хОу), т. е. уничтожает две степени свободы, но допускает поступательное перемещение присоединяемого тела по прямой, перпендикулярной плоскости двух стержней (по оси у — одна степень свободы), и повороты вокруг трех осей, проходящих, например, через общий шарнир (три степени свободы). Статическая ха­рактеристика: в связи может возникать реактивная сила, лежащая в плоскости стержней и проходящая через общий шарнир, которая может быть разложена на две составляющие.

Два параллельных стержня (плоско-подвижная связь с двумя по­воротами— рис. 2, в). Кинематическая характеристика: связь унич­тожает поступательное перемещение присоединяемого тела вдоль стерж­ней (по оси у) и поворот в их плоскости (в плоскости yOz), т. е. унич­тожает две степени свободы, но допускает поступательное перемещение присоединяемого тела по направлению, перпендикулярному стержням (в плоскости хОz — две степени свободы), и два поворота вокруг вер­тикальной и горизонтальной осей, например проходящих через два шар­нира (вокруг осей у и z — две степени свободы). Статическая характе­ристика: в связи могут возникать две реактивные силы вдоль стержней, которые могут быть сведены к силе, действующей параллельно стерж­ням, и паре сил в плоскости стержней.

Три стержня, не лежащие в одной плоскости, с общим шаровым шарниром на одном из их концов (неподвижная шаровая связь или шаровой шарнир – рис. 2, г). Кинематическая характеристика: связь уничтожает все три поступа­тельные перемещения присо­единяемого тела, т. е. уничто­жает три степени свободы, но допускает повороты вокруг трех осей, проходящие через общий шарнир (три степени свободы). Статическая харак­теристика: в связи может воз­никать реактивная сила, про­ходящая через общий шарнир, которая может быть разложе­на на три составляющие.

5. Три параллельных стерж­ня, не лежащих в одной плос­кости (плоско-подвижная связь с одним поворотом — рис. 2, д). Кинематическая характе­ристика: связь уничтожает по­ступательное перемещение при­соединяемого тела вдоль стер­жней (по оси у) и два поворо­та вокруг осей х и z, т. е. уни­чтожает три степени свободы, но допускает поступательное перемещение присоединяемого тела в плоскости, перпендику­лярной стержням (в плоскости хОz, — две степени свободы), и поворот вокруг оси, парал­лельной стержням (парал­лельно оси у одна степень свободы). Статическая характеристика: в свя­зи могут возникать три реактивные силы по направлению трех стерж­ней, которые могут быть сведены к силе, действующей, например, вдоль углового стержня, и к двум парам сил в плоскостях хОу и zOy.

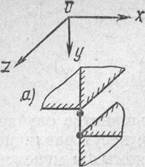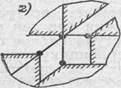
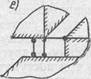
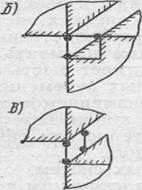
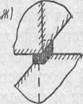
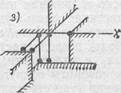
Рис. 2

Три стержня в одной плоскости, из которых два параллельны, а третий имеет общий шаровой шарнир с одним из них (линейно-подвиж­ная связь с двумя поворотами — рис. 2, е). Кинематическая характе­ристика: связь уничтожает поступательные перемещения и поворот при­соединяемого тела в плоскости стержней (в плоскости хОу), т. е. унич­тожает три степени свободы, но допускает поступательное перемещение по прямой, перпендикулярной плоскости стержней (одна степень свобо­ды), и два поворота, например, вокруг осей х и у (две степени свободы). Статическая характеристика: в связи могут возникать реактивные силы вдоль стержней, которые могут быть сведены к силе и паре сил в плос­кости стержней.

Припайка (неподвижная связь без поворотов — рис. 2, ж). Кинематическая характеристика: связь уничтожает все перемещения присоединяемого тела, т. е. уничтожает все шесть степеней свободы. Статическая характеристика: в связи могут возникать три реактив­ные силы по направлениям координатных осей и три реактивных момента в координатных плоскостях. Припайка эквивалентна шести стержням.

Кроме рассмотренных простых связей возможны и более сложные, получаемые из простых добавлением стержней. Так, например, если к связи (рис. 2, г) добавить два стержня, препятствующих поворотам вокруг двух осей, получим так называемый цилиндрический шарнир, до­пускающий поворот только вокруг одной оси х, проходящей через шаро­вые шарниры на концах пяти стержней (рис. 2, з).