Затухающие колебания инженерных сооружений
Подставляя вместо сил R, F и X их выражения (2)—(4), деля уравнение на m и меняя знаки, получаем обыкновенное однородное линейное дифференциальное уравнение второго порядка:
у" + 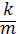 y′ +
y′ + 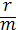 y = 0. (5)
y = 0. (5)
Решение этого дифференциального уравнения можно представить так:
у = a0e-kt/2m sin (wt + 𝜑0). (6)
Здесь е — основание натуральных логарифмов (e 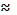 2,72); w — круговая частота свободных колебаний, т. е. число циклов колебаний в течение 2
2,72); w — круговая частота свободных колебаний, т. е. число циклов колебаний в течение 2 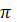 секунд;
секунд;
w = 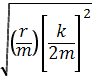 ; (7)
; (7)
α0 — начальная амплитуда свободных колебаний;
α0 = 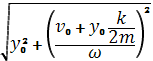 ; (8)
; (8)
𝜑0 – начальная фаза свободных колебаний, характеризующая отклонение
перемещение;
𝜑о = arcsin 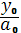 ;
;
y0 – начальное перемещение;
y0 = а0 sin𝜑0; (9)
v0 — начальная скорость массы.
Период, т. е. продолжительность полного цикла колебаний в секундах, составляет Т = 2  / w. (10)
/ w. (10)
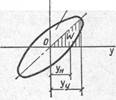
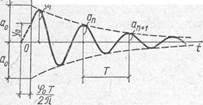
Рис. 3
Рис. 2
Рис. 3
График свободных затухающих колебаний показан на рис. 2.
Найдем натуральный логарифм отношения двух последовательных однозначных амплитуд свободных колебаний, который обозначим δ:
δ = 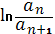 = αТ. (11)
= αТ. (11)
Эта величина, характеризующая скорость затухания колебаний, н а з ы- вается логарифмическим декрементом колебаний, а величина α = k/(2m) — коэффициентом затухания.
В системе с затуханием зависимость между какой-либо внешней силой Р и перемещением у нелинейна, поэтому при каждом цикле колебаний на диаграмме Р — у получается замкнутая кривая, называемая петлей гистерезиса (рис. 3). Можно принять, что при гармонических колебаниях петля гистерезиса имеет форму эллипса с центром в начале координат. Отношение работы неупругих сопротивлений ΔW за цикл к работе W упругих сил за четверть цикла, т. е. на пути от ненагруженного до крайнего деформированного состояния системы, называется коэффициентом поглощения энергии.
На графике рис. 3 работа ΔW выражается площадью эллипса, а работа W — площадью заштрихованного треугольника.
Если не учитывать затухания колебаний, то из формул (6) – (9) получим:
y = a sin (wt + 𝜑0), (12)
w = 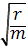 = =
= = 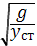 , (13)
, (13)
а = 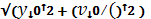 , (14)
, (14)
𝜑0 = arcsin (y0/а). (15)
При этом уст = δ11Q – статическое перемещение системы от груза Q = mg.
График уравнения (12) представлен на рис. 4.
Величина а, характеризующая размах колебания, называется амплитудой колебаний. Величина 𝜑0 является начальной фазой колебаний.
На графике рис. 4 величина периода Т, имеющая размерность времени, показана как отрезок времени между двумя соседними однозначными амплитудами.
Частота колебаний, т. е. число полных циклов колебаний в 1 с, выражается в герцах и составляет
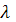 = 1/Т = w/(2
= 1/Т = w/(2 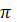 ),
),
где Т должно быть выражено в секундах.
Из формулы (13) видно, что частота уменьшается с увеличением статического прогиба упругой системы, т. е. с уменьшением ее жесткости. Частота убывает также с увеличением массы.
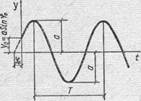
Рис. 4
Технической частотой n называют число колебаний в минуту. Техническая частота выражается формулами:
n = 60λ = 60/T = 30а)/я = (30/ 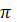 )
) 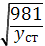
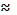 300/
300/  .
.
Как показывает формула (7), затухание приводит к уменьшению частоты свободных колебаний. Однако второй член под корнем этого выражения, как правило, во много раз меньше первого, поэтому практически можно считать, что затухание не оказывает влияния на частоту свободных колебаний.
Дата добавления: 2016-11-29; просмотров: 1492;











