Мгновенное значение частоты ФМ-колебания равно
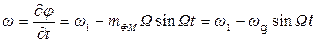 , (2.25)
, (2.25)
ωg = mФМ W , (2.26)
где ωg – девиация частоты колебания.
Процесс получения ФМ-сигнала показан на рисунке 2.7, а векторное представление – на рисунке 2.8.
Сравнение выражений (2.19) и (2.24) показывает, что при гармоническом модулирующем сигнале выражение, описывающее ЧМ-колебания, отличается от такового для ФМ-колебания только фазой гармонической функции, определяющей изменение полной фазы носителя. Векторное представление ФМ-колебания (рисунок 2.8) такое же, как и для ЧМ-колебания (см. рисунок 2.5), т.е. это будет качающийся вектор с постоянной длиной Uω1 и с максимальным углом отклонения в обе стороны mФМ =qmax.
На рисунке 2.9 приведены зависимости индекса модуляции и девиации частоты ФМ-колебания от частоты модулирующего сигнала W.
\ 
| Рисунок 2.7 – Процесс получения ФМ-сигнала | Рисунок 2.9 – Зависимость mФМ и ωg от W при ФМ |
В соответствии с выражениями (2.23) и (2.26) индекс модуляции mФМ от W не зависит и определяется только величиной амплитуды модулирующего сигнала UW, девиация частоты ωg прямо пропорциональна частоте W модулирующего сигнала.
2.3.1 Различие ЧМ- и ФМ-колебаний. Итак, при модуляции одним тоном по характеру колебания и его свойствам нельзя заключить, с какой модуляцией мы имеем дело – с частотной или фазовой. Различие между ЧМ и ФМ проявляется при изменении частоты модуляции или при одновременной модуляции полосой частот.
При ЧМ величина девиации частоты ωg остается постоянной при изменении частоты модуляции W. Величина же индекса модуляции mЧМ =qmax с увеличением частоты модуляции W убывает (см. рисунок 2.6).
При ФМ величина индекса модуляции mФМ =qmax остается постоянной при изменении частоты модуляции W. Девиация частоты ωg изменяется прямо пропорционально частоте модуляции W (см. рисунок 2.9).
Если модуляция осуществляется не одним гармоническим, а сложным сигналом, то структура модулированного колебания будет различной для ЧМ и ФМ.
В случае ЧМ медленным изменениям модулирующего сигнала (т.е. низким частотам его спектра) будут соответствовать очень большие значения
mЧМ =qmax(см. рисунок 2.6). В случае ФМ медленным изменениям модулирующего сигнала будут соответствовать очень малые значения девиации частоты ωg (см. рисунок 2.9).
Наконец, Чм и ФМ различаются по способам их технического осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебания задающего генератора. В случае ФМ задающий генератор вырабатывает стабильную частоту, а фаза модулируется в одном из последующих каскадов передатчика.
2.4 Спектры сигнала с угловой модуляцией
Рассмотрим случай модуляции одним тоном. Выражение для сигнала, модулированного по частоте или фазе, запишем в виде
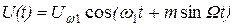 . (2.27)
. (2.27)
Произведя преобразования, получим
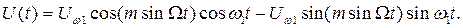 (2.28)
(2.28)
Рассмотрим сначала спектр сигнала, когда m<<1. Тогда можно считать, что

Подставив эти приближенные равенства в формулу (2.28), получим
|
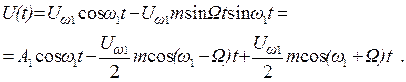
Сравнивая выражения (2.7) и (2.29), заключаем, что спектр ЧМ или ФМ-сигнала при малом значении m состоит, как и спектр АМ сигнала, из несущей частоты ω1 и двух боковых частот ω1+W и ω1-W. Единственное отличие заключается в сдвиге фазы сигнала нижней боковой частоты (знак минус) на 1800 относительно его положения при АМ. Спектр амплитуд сигнала с угловой модуляцией при m<<1 показан на рисунке 2.10.
Так как фаза отдельных составляющих сигнала этой диаграммой не учитывается, то характер диаграммы такой же, как и в случае АМ (см. рисунок 2.2,а). Отметим, что в данном случае влияние индекса модуляции m совпадает с влиянием коэффициента глубины модуляции mАМ, а ширина спектра
∆ω=2Ω. (2.30)
Последний вывод говорит о том, что при очень малых величинах девиации частоты ωg = mW (по сравнению с W) ширина спектра от величины ωg не зависит. Векторное изображение рассмотренного случая дано на рисунке 2.11.
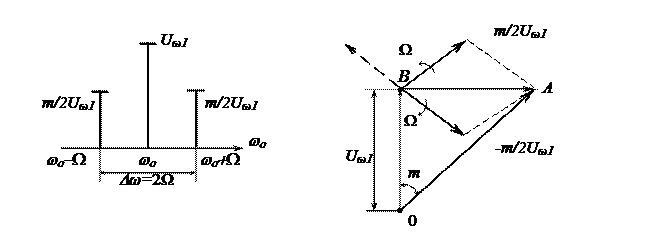
| Рисунок 2.10 – Спектр амплитуд сигнала с угловой модуляцией при m<<1 | Рисунок 2.11 – Векторное изображение сигнала с угловой модуляцией при m<<1 |
Оно отличается от векторного изображения АМ-сигнала (см. рисунок 2.3) только направлением вектора, изображающего составляющую нижней боковой частоты. В результате вектор модуляции BA всегда перпендикулярен к направлению вектора Uω1. Вектор ОА, изображающий результирующее колебание, изменяется по фазе и по амплитуде. Однако при m=qmax<<1 амплитудными изменениями можно пренебречь, вследствие чего модуляция может, в первом приближении, рассматриваться как чисто угловая.
Обратимся к рассмотрению более общего случая, когда m – любая величина. Для этого функции sin(msinW t) и cos(msinW t)из выражения (2.28) разложим в тригонометрические ряды.
В теории Бесселевых функций доказываются следующие соотношения:
|
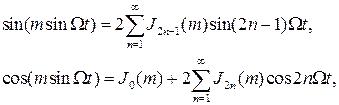
где Jn(m) – Бесселева функция первого рода n-го порядка от аргумента m.
С учётом формул (2.31) выражение (2.28) перепишем в виде
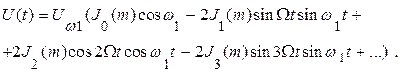
Заменив в этом выражении произведения косинусов и синусов суммами, окончательно получим
|

Таким образом, при угловой модуляции спектр сигнала состоит из бесконечного числа боковых частот, отличающихся от несущей частоты ω1 на ± nW.
Примерный вид спектра сигнала с угловой модуляцией одним тоном W при m=3и Uω1=1 В представлен на рисунке 2.12. По мере удаления от ω1 амплитуды боковых составляющих уменьшаются.
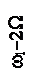
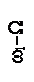
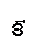
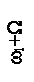
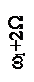
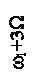
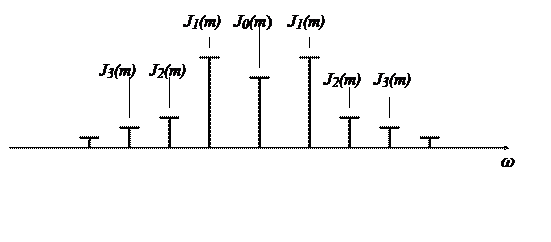
Рисунок 2.12 – Спектр сигнала с угловой модуляцией при m=3 и W=const
Хотя теоретически спектр колебаний с угловой модуляцией бесконечен, практически он ограничен. Практическую ограниченность спектра сигнала с угловой модуляцией позволяют усмотреть свойства Бесселевых функций. При n>m функция Jn(m) (таблица 2.1) имеет малые значения. Это означает, что амплитуды боковых составляющих в рассмотренном спектре сигнала с угловой модуляцией становятся очень малыми и ими можно пренебречь. При увеличении m происходит перераспределение энергии. Все большая часть энергии переносится боковыми составляющими.
Таблица 2.1 – Значения Бесселевых функций Jn(m)
| m | J0 | J1 | J2 | J3 | J4 | J5 | J6 | J7 |
| 0,2 | 0,99 | 0,10 | — | — | — | — | — | — |
| 0,4 | 0,96 | 0,20 | 0,02 | 0,001 | — | — | — | — |
| 0,6 | 0,91 | 0,29 | 0,044 | 0,004 | — | — | — | — |
| 1,0 | 0,76 | 0,44 | 0,115 | 0,02 | 0,002 | — | — | — |
| 2,0 | 0,22 | 0,58 | 0,35 | 0,13 | 0,034 | — | — | — |
| 5,0 | 0,18 | 0,33 | 0,05 | 0,36 | 0,39 | 0,26 | 0,13 | 0,05 |
| 10,0 | 0,25 | 0,06 | 0,25 | 0,06 | 0,22 | 0,23 | 0,015 | 0,022 |
Этим и определяется практическая ширина спектра сигнала с угловой модуляцией, т.е.
| ∆ω=2nW=2mW=2(m+1) W = 2ωg ; | ||
| при m>5 | ∆ω=2nW@2mW=2ωg . |
Как следует из (2.33), практически ширина полосы равна удвоенной девиации частоты. Полоса частот, равная 2ωg, называется полосой качания, так как в процессе модуляции несущая частота может принимать любое мгновенное значение внутри интервала ω 1 ± ωg.
Векторная диаграмма сигнала с угловой модуляцией представлена на рисунке 2.13.

Рисунок 2.13 – Векторное представление сигнала с угловой модуляцией
На диаграмме показаны вектор основной частоты ω1, первая (ω1±W), вторая (ω1±2W) и третья (ω1±3W) пары боковых частот. Равнодействующая первой пары боковых частот направлена перпендикулярно к вектору основной частоты, второй – вдоль вектора основной, третьей – перпендикулярно и т.д. В результате сложения всех этих векторов получается вектор, вращающийся по дуге окружности с частотой W на угол ±m радиан.
Как указывалось выше, различие между ЧМ- и ФМ-сигналами при модуляции одним тоном проявляются только при изменении частоты модуляции W. Посмотрим, как будут изменяться спектры ЧМ- и ФМ-сигналов в этом случае.
Для ЧМ-сигналов при m>>1 ширина спектра в соответствии с выражениями (2.19) и (2.33) равна
2ωg =2кЧМUW , (2.34)
т.е. зависит только от амплитуды UW модулирующего сигнала. Число спектральных линий (гармонических составляющих) практического спектра ЧМ-колебаний с учетом (2.19), изменяется обратно пропорционально частоте W, т.е.
n @ m= ωg /W . (2.35)
Поэтому, например, при увеличении частоты модуляции W и постоянной амплитуде UW число спектральных составляющих уменьшается (2.35), а практическая ширина спектра ЧМ-колебаний остается постоянной, ибо
∆ω = 2nW @ 2mW = 2ωg (2.36)
И, наоборот, с уменьшением частоты W число спектральных составляющих возрастает (2.35). При этом практическая ширина спектра в соответствии с (2.36) опять-таки остается постоянной.
Для ФМ-колебаний при m>>1 ширина спектра в соответствии с выражениями (2.23), (2.26) и (2.33) равна
∆ω=2nW@2mW=2kфмUWW , (2.37)
т.е. она зависит как от амплитуды UWmax, так и от частоты W модулирующего сигнала. При ФМ число спектральных линий спектра при UW=const остается неизменным. С изменением W при UW=const изменяется интервал между соседними гармоническими составляющими и общая ширина спектра ФМ-сигнала также изменится.
2.5 Сравнение АМ-, ЧМ- и ФМ- сигналов
Сравним указанные виды модуляции по их двум основным характеристикам: средней за период высокой частоты мощности и ширине спектра.
Для АМ-сигналов средняя за период высокой частоты мощность изменяется, так как изменяется амплитуда сигнала. Эта мощность в максимальном режиме в (1+mАМ)2 раз больше мощности молчания. Ширина спектра АМ сигнала зависит от величины максимальной частоты модуляции и равна 2Wmax.
Для ЧМ-сигналов средняя за период высокой частоты мощность постоянна, так как амплитуда колебаний неизменна (Uω1= const). Ширина спектра ЧМ-сигнала, равна 2ωg, зависит только от амплитуды модулирующего сигнала и не зависит от его частоты.
Для ФМ-колебаний средняя за период высокой частоты мощность также неизменна, ибо Uω1=const. Ширина спектра равна 2mW=2ωg, и зависит как от амплитуды модулирующего сигнала, так и от его частоты.
Таким образом, практическая ширина спектра колебаний с угловой модуляцией в m раз больше ширины спектра АМ-колебаний.
2.6 Одновременная модуляция по амплитуде и по частоте
В ряде случаев возникает необходимость в передаче двух сообщений с помощью одного носителя. Тогда одним сообщением носитель модулируют по частоте, а другим – по амплитуде. Наиболее простой по составу спектр сигнала с двойной модуляцией получится при гармоническом законе изменения, как частоты, так и амплитуды. Пусть по частоте носитель модулируется сообщением с частотой W1, а по амплитуде – с частотой W2. Тогда частота и амплитуда носителя будут изменяться в соответствии с выражениями
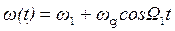 , (2.38)
, (2.38)
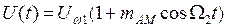 . (2.39)
. (2.39)
Модулированное по частоте напряжение было получено выше при постоянной амплитуде Uω1 (2.32). При изменении амплитуды в этом выражении следует заменить постоянную амплитуду Uω1 изменяющейся в соответствии с (2.39). Тогда получим:
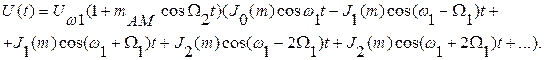
По сравнению с напряжением, модулированным только по частоте, здесь появляются дополнительные составляющие двух видов:
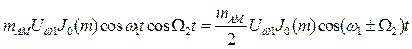 (2.40)
(2.40)
и
|
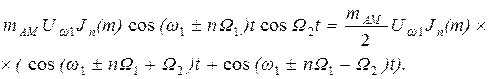
Чтобы яснее выявить спектральный состав сигнала, предположим сначала, что W1>>W2, т.е. изменение амплитуды происходит значительно медленнее, чем изменение частоты. Тогда можно считать, что в спектре частотно-модулированного сигнала около несущего колебания с частотой ω1 и боковых составляющих с частотами ω1±nW1 появилось дополнительно по два спутника с частотами, отличающимися на ±W2. Спектр такого сигнала показан на рисунке 2.14.

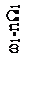
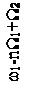
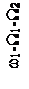
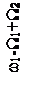
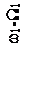
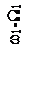

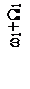
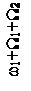
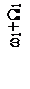
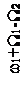
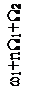
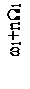
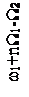

Рисунок 2.14 – Спектр сигнала при одновременной модуляции
по частоте и амплитуде при W1>>W2
Для систем телемеханики интерес представляет второй случай, а именно спектр сигнала при W1<<W2. Тогда можно считать, что у каждой из трех спектральных линий АМ сигнала (несущей с частотой ω1, нижней (ω1-W2) и верхней (ω1+W2) боковых составляющих) появились дополнительно по две боковые дискретные полосы: верхняя с частотами +nW1 и нижняя с частотами -nW1. Спектр сигнала для этого случая двойной модуляции показан на рисунке 2.15.
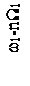
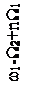
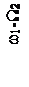
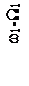

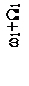
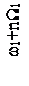
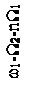
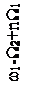
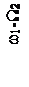
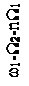

Рисунок 2.15 – Спектр сигнала при одновременной модуляции
по частоте и амплитуде при W1<<W2
Практически необходимая ширина спектра сигнала примерно равна сумме необходимых спектров только при амплитудной модуляции DωАМ и только при частотной модуляции DωЧМ (рисунки 2.14, 2.15). При малом индексе частотной модуляции (mЧМ <1) необходимая ширина спектра сигнала лишь немногим больше, чем при амплитудной модуляции.
3 ИМПУЛЬСНАЯ МОДУЛЯЦИЯ
При импульсных видах модуляции в качестве носителя используется, как правило периодическая последовательность прямоугольных импульсов, которая описывается рядом Фурье в следующем виде:
|
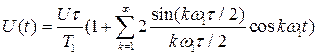
где 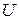
| – амплитуда импульса, |
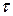
| – длительность импульса; |
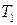
| – период следования импульсов. |
Учитывая, что угловая частота импульсной последовательности 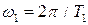 , а отношение T1/t =Q – скважность импульсной последовательности, выражение (3.1) представим в виде:
, а отношение T1/t =Q – скважность импульсной последовательности, выражение (3.1) представим в виде:
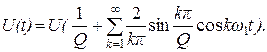 (3.2)
(3.2)
Как следует из выражений (3.1) и (3.2), изменяя модулирующим сообщением амплитуду, длительность импульса, период следования, а также время появления импульсов относительно тактовых точек можно получить соответственно амплитудно-импульсную модуляцию (АИМ), широтно-импульсную модуляцию (ШИМ), частотно-импульсную(ЧИМ) и фазоимпульсную модуляцию (ФИМ).
3.1 Амплитудно-импульсная модуляция
При АИМ амплитуда импульсов изменяется по закону передаваемого (модулирующего) сигнала.
Рассмотрим простейший случай АИМ одним тоном, т.е. когда модулирующий сигнал описывается выражением
|
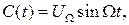
a немодулированная последовательность импульсов представляется рядом Фурье (3.2).
Различают АИМ первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 высота импульса в пределах его длительности (t) изменяется по закону модулирующего напряжения. При АИМ-2 высота импульса зависит лишь от значения сигнала в тактовой точке.
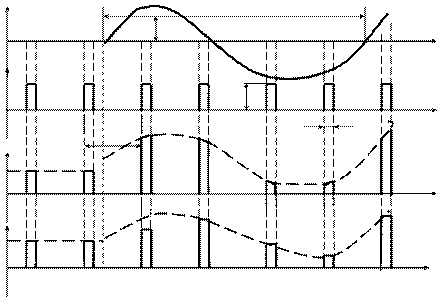
Временные диаграммы АИМ-1 и АИМ-2 сигналов приведены на рисунке 3.1.
 C(t) Т
C(t) Т
UW
0 t
U(t)
U
0 t
T1 t
АИМ-1
0 t
АИМ-2
0 t
Рисунок 3.1 – Временные диаграммы АИМ-1 и АИМ-2 сигналов
В соответствии с определением АИМ амплитуда импульсов U при
АИМ-1 будет изменяться по следующему закону:
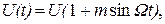 (3.4)
(3.4)
| – коэффициент глубины модуляции, | ||||
| k | – коэффициент пропорциональности, устанавливающий связь между амплитудой модулирующего сообщения и изменением амплитуды импульсов носителя. |
Подставив (3.4) в (3.3), получим выражение для АИМ-1 в виде
|
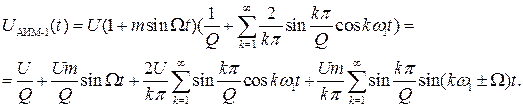
Cравнение выражений (3.3) и (3.5) показывает, что в случае модуляции одним тоном W спектр амплитуд модулированной последовательности импульсов отличается от спектра немодулированной последовательности наличием составляющей с частотой модуляции W и боковых составляющих с частотами kω1±W возле каждой гармоники спектра немодулированной последовательнос-ти, представленного на рисунке 3.2.
 |
 ½Ак½
½Ак½

 Q=3
Q=3
КФНЧ
 | |||
 |



 U
U



 Q
Q
W 


 W 2p/t 4p/t
W 2p/t 4p/t









 W W W W
W W W W

|
|
|
|
|
|


 ω
ω
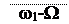 | 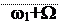 |
Рисунок 3.2 – Спектр амплитуд АИМ-1 сигнала
Появление в спектре составляющей с частотой W можно объяснить следующим образом. Если у последовательности импульсов постоянной высоты среднее значение также постоянно, то у последовательности импульсов, модулированных по амплитуде с частотой W (см. рисунок 3.1), и среднее значение изменяется с частотой W. Важно заметить, что ширина спектра последовательности импульсов, которую нужно сохранить при передаче, практически не изменяется в результате модуляции по амплитуде (появление боковых частот kω1±W не сказывается на ширине спектра). Действительно, в обоих случаях необходимая ширина спектра определяется длительностью импульсов (t), которая при АИМ не изменяется:
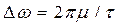 . (3.6)
. (3.6)
На практике в большинстве случаев принимают m=1, т.е. необходимая полоса частот определяется первым лепестком спектра, где сконцентрировано около 90% энергии всего сигнала. Так как в спектре есть модулирующая частота W, то выделить в приемнике первичный сигнал можно фильтром низких частот (см. рисунок 3.2), но для неискаженного выделения необходимо выполнить условие
W<ω1-W или ω1>2W.(3.7)
Условие (3.7) соответствует требованиям теоремы Котельникова, рассмотренной ранее.
Если последовательность импульсов модулируется не простым гармоническим сигналом, а сигналом, ширина спектра которого лежит в пределах от Wmin до Wmax, то в спектре модулированного сигнала появляются полосы частот Wmin¸Wmax и kω1±(Wmin¸Wmax), как показано на рисунке 3.3.
 ½Ак½
½Ак½
 А1
А1

 Q = 3
Q = 3
А2










 А0 А4 А5
А0 А4 А5























 2p/t
2p/t











 А6
А6
|
|
|

 |


|











 ω .
ω .
|
 |  |

Рисунок 3.3 – Спектр амплитуд АИМ-1 сигнала при модуляции
сложным сообщением
Выражение для сигнала АИМ-2 при модуляции одним тоном может быть получена в виде:
|
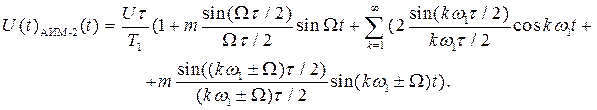
Спектр амплитуд АИМ-2 показан на рисунке 3.4.

 ½Ак½
½Ак½

 Q=3
Q=3



 Ao
Ao





W 




 W 2p/t 4p/t
W 2p/t 4p/t










 W W
W W
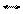
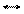

|
|
|
|
|
|


|
|
|


Рисунок 3.4 – Спектр амплитуд АИМ-2 сигнала
Спектральный состав модулированной последовательности импульсов при АИМ-2 не отличается от спектрального состава при АИМ-1. Несколько изменяются только амплитуды боковых составляющих и составляющих с частотами спектра модулирующего сообщения (3.8).
3.2 Фазоимпульсная модуляция
При ФИМ по закону изменения передаваемого сигнала с(t)=UWsin(Wt) изменяется величина временного сдвига относительно тактовых точек (рисунок 3.5)

Рисунок 3.5 – Временные диаграммы ФИМ-сигнала
Если у немодулированного импульса фронт соответствует моменту времени -τ/2, а спад – моменту времени +τ/2, то для модулированного импульса эти моменты будут (рисунок 3.6)
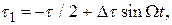 (3.9)
(3.9)
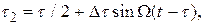 (3.10)
(3.10)
где ∆τ =kUW – наибольшее смещение фронта.
В выражении (3.10) время t заменено временем t-τ, так как спад импульса смещен относительно фронта на интервал времени, равный длительности импульса τ.

Рисунок 3.6 – ФИМ-сигнал на одном интервале времени
Для записи модулированного напряжения в формуле (3.1) для немодулированной последовательности, во-первых, заменим τ на τ2-τ1, чтобы учесть смещение фронта и спада импульса, во-вторых, время t заменим временем
t-(τ2+τ1)/2, чтобы учесть смещение центра импульса относительно тактовой точки. Тогда
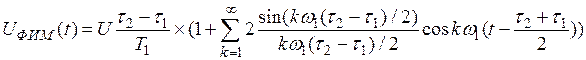
или, заменив произведение синуса на косинус по формуле тригонометрических преобразований и подставив T1ω1=2p, найдем
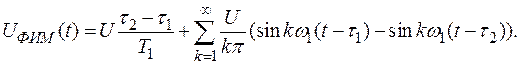 (3.11)
(3.11)
Заменив в (3.11) τ1 и τ2 согласно (3.9) и (3.10), получим
|
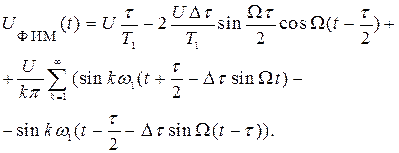
В выражении (3.12) 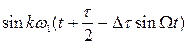 и
и 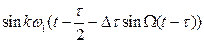 заменим рядами Фурье, коэффициентами которых являются функции Бесселя, т.е.
заменим рядами Фурье, коэффициентами которых являются функции Бесселя, т.е.
|
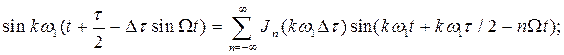
|
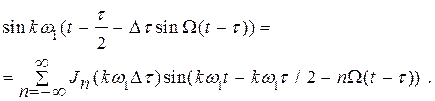
Подставив (3.13) и (3.14) в (3.12) и заменив разность синусов по тригонометрическим формулам, получим
|
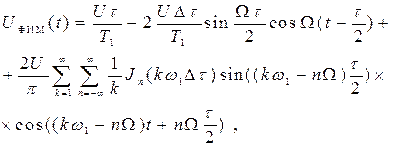
где ω1Dt=mФИМ – индекс модуляции при ФИМ.
Из анализа выражения (3.15) следует, что спектр сигнала при ФИМ содержит постоянную составляющую, составляющую с частотой модулирующего сигнала W, основную гармонику с частотой ω1(k=1) и кратные ей высшие гармоники с частотами kω1, вокруг которых размещаются полосы боковых гармоник с частотами kω1±nW (рисунок 3.7).

Рисунок 3.7 – Спектр ФИМ-сигнала
В заключение следует отметить, что сигнал ФИМ относится к широкополосным и его спектр намного шире спектра сообщения и простирается от постоянной составляющей до частоты ωB=2p /t, а следовательно, необходимая полоса частот
DωФИМ=2p /t. (3.16)
Доля мощности, заключенная в составляющих с частотами выше ωB, настолько мала, что эти составляющие можно не учитывать.
3.3 Широтно-импульсная модуляция
При ШИМ длительность импульсов изменяется пропорционально модулирующему сигналу, а их амплитуда остается постоянной.
Рассмотрим модуляцию одним тоном, т.е. когда модулирующий сигнал описывается выражением
C(t)=UW sinWt .
Дата добавления: 2021-02-19; просмотров: 612;











