Полная фаза модулированного колебания определяется в виде
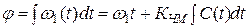 . (2.18)
. (2.18)
Отсюда видно, что при ЧМ имеет место изменение фазы колебания, т.е. ФМ.
Подставив (2.18) в (2.16), получим выражение для частотно-модулирован-ного сигнала
|
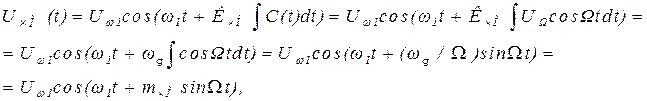
| где ωg =кЧМ×UW | – девиация частоты, т.е. максимальное отклонение частоты от значения ω1; |
| mЧМ= ωg /W | – индекс частотной модуляции. |
Индекс частотной модуляции фактически равен максимальному отклонению фазы ЧМ-колебания, т.е. mЧМ =qmax. Он не зависит от средней ω1 (немодулированной) частоты, а определяется исключительно величиной девиации частоты ωg и модулирующей частотой W.
Векторное представление ЧМ-колебания для рассмотренного случая показано на рисунке 2.5. Вектором Uω1 показано немодулированное высокочастотное колебание. Чтобы этот вектор был неподвижен, предполагаем, что ось времени вращается по часовой стрелке с угловой скоростью ω1. Приращение фазы вектора Uω1 изменяется по гармоническому закону с частотой W. Максимальное изменение фазы определяется индексом модуляции mЧМ, т.е. вектор Uω1 отклоняется в обе стороны на угол mЧМ. Например, если mЧМ =1, то это означает, что вектор Uω1 отклоняется в обе стороны на один радиан. На практике с целью повышения помехоустойчивости приема при использовании ЧМ применяются большие значения mЧМ.
На рисунке 2.6 приведены зависимости индекса модуляции mЧМ и девиации частоты ωg ЧМ-колебания от частоты модулирующего сигнала W.
Как видно из рисунка 2.6 и соответствующих выражений, ωg от W не зависит и определяется только величиной UW, а mЧМ с увеличением W убывает.
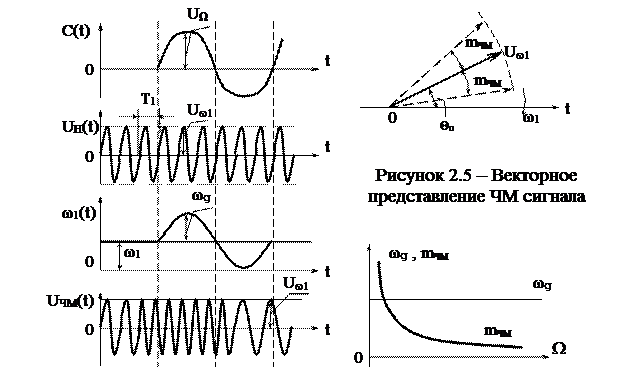
Рисунок 2.4 – Процесс получения Рисунок 2.6 – Зависимость
частотно –модулированного сигнала mЧМ и ωg от W при ЧМ
2.3 Фазовая модуляция (ФМ)
При фазовой модуляции по закону модулирующего сигнала изменяется начальная фаза.
Рассмотрим частный случай, когда модулирующий сигнал является гармоническим, т.е.
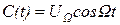 , (2.20)
, (2.20)
а носитель описывается выражением
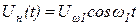 . (2.21)
. (2.21)
Тогда полная фаза ФМ-колебания в соответствии с определением ФМ запишется в виде
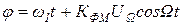 . (2.22)
. (2.22)
Обозначим
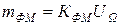 , (2.23)
, (2.23)
| где mФМ | – индекс фазовой модуляции, т.е. максимальное отклонение фазы колебания; |
| кФМ | – коэффициент пропорциональности, определяющий связь между модулирующим сигналом и изменением фазы колебания. |
Подставив (2.22) в (2.21), получим выражение для ФМ в виде
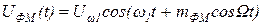 . (2.24)
. (2.24)
Дата добавления: 2021-02-19; просмотров: 470;











