ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА 10.1
Заданы схема сети напряжением 10 кВ, приведенная на рис. 10.24, и параметры сети: длины участков сети, их марки проводов и номинальные мощности трансформаторов 10/0,38 кВ. В центре питания установлен трансформатор 110/10 кВ со ступенями РПН δUCT = 1,78 %. Суммарный ток ЦП в режиме наибольших нагрузок со стороны 10 кВ
Iнб =30 A, cosφ = 0,92. Допустимые отклонения напряжения у электроприемников
δUдоп = ±5 %. Отношение наименьшей нагрузки к наибольшей m = 0,25. Потерю напряжения в режиме наибольших нагрузок от шин 0,38 кВ ТП до ближайшего приемника принять ΔU”hн.б= 0 %, а до наиболее удаленного — ΔU”hн.у= 5 %. Коэффициент чувствительности регулятора напряжения принять n= 1,3.
Выбрать режим регулирования напряжения в ЦП и ответвления трансформаторов ТП.
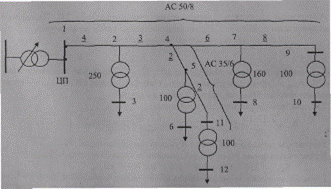
Рис. 10.24. Заданная схема сети.
Решение
1. Расчет параметров трансформаторных подстанций 10/0,38 кВ и участков сети.
По заданным маркам проводов, используя справочные данные, находим удельные сопротивления r0 и x0. По заданным длинам линий находим активные и реактивные сопротивления. Заносим их в табл. 10.5 и указываем на схеме рис. 10.25.
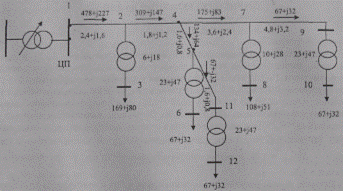
Рис.10.25. Схема сети с параметрами участков и потоками мощности.
Аналогично поступаем с параметрами трансформаторов ТП. Паспортные данные приведены в табл. 10.6. Расчет сопротивлений ведем по формулам:
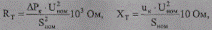
где ΔРК — потери короткого замыкания, кВт; UK — напряжение короткого замыкания, %; SH0M — номинальная мощность трансформатора, кВА; UНOM — номинальное напряжение обмотки высшего напряжения, кВ.
Так, для трансформатора 100 кВА имеем:
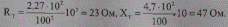
Результаты заносим в табл. 10.5 и указываем на схеме рис. 10.25.
Найдем суммарную номинальную мощность трансформаторов ТП:
SHOMΣ = 250+ 100+ 160+ 100+ 100 = 710кВА.
По заданному току трансформатора ЦП в режиме наибольших нагрузок Iцп.нб = 30 А вычислим токи всех трансформаторов ТП, приняв их пропорциональными номинальным мощностям трансформаторов Siном:
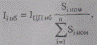
где n — число ТП, подключенных к ЦП.
Так, для трансформатора 2—3: I2-3 = 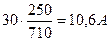
Таблица 10.5
Параметры участков сети
| Номер участка сети | R, Ом | X, Ом | Рнб, кВт | Qнб,квар | 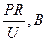
| 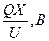
| ΔU, В | ΔU,% | |
| Линии | 1—2 | 2,4 | 1,6 | 114,7 | 36,3 | 1,51 | |||
| 2—4 | 1,8 | 1,2 | 55,6 | 17,6 | 73,2 | 0,73 | |||
| 4—5 | 1,6 | 0,8 | 21,4 | 5,1 | 26,5 | 0,26 | |||
| 4—7 | 3,6 | 2,4 | 19,9 | 82,9 | 0,83 | ||||
| 5—11 | 1,6 | 0,8 | 10,7 | 2,6 | 13,4 | 0,13 | |||
| 7—9 | 4,8 | 3,2 | 32,2 | 10,2 | 42,4 | 0,42 | |||
| Трансформаторы | 2—3 | 101,4 | 245,4 | 2,45 | |||||
| 5—6 | 3,04 | ||||||||
| 7—8 | 2,51 | ||||||||
| 9—10 | 3,04 | ||||||||
| 11—12 | 3,04 |
Таблица 10.6
Паспортные данные трансформаторов 10/0,38 кВ
| Sном кВА | uк,% | ΔРк,кВт |
| 4,7 | 2,27 | |
| 4,5 | 2,65 | |
| 4,5 | 3,7 |
Таблица 10.7
Режимные параметры трансформаторов ТП
| Номер трансформатора | Ток 1и6, А | Мощности | |
| Рнб,кВт | Qнб, квар | ||
| 2—3 | 10,6 | ||
| 5—6 | 4,2 | ||
| 7—8 | 6,8 | ||
| 9—10 | 4,2 | ||
| 11—12 | 4,2 |
Результаты занесем в табл. 10.7
По заданному cosφ = 0,92 вычислим активные и реактивные мощности ТП. Так, для  трансформатора 2—3 получим:
трансформатора 2—3 получим:
Результаты вычислений занесем в табл. 10.7 и укажем на схеме рис. 10.25.
2. Определение зоны нечувствительности автоматического регулятора напряжения трансформатора в центре питания.
С использованием заданных ступени регулирования на трансформаторе ЦП δUCT=1,78 % и коэффициента чувствительности n=1,3 по формуле (10.37) найдем зону нечувствительности  регулятора:
регулятора:
3. Расчет режимов распределительной сети.
Найдем потоки мощности на каждом участке сети без учета потерь мощности и нанесем их на схему рис. 10.25 и занесем в табл. 10.5. Найдем потери напряжения в вольтах и в процентах, после чего также занесем их в табл. 10.5. Так, для участка 1—2 будем иметь:
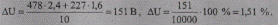
По найденным потерям напряжения на участках сети вычислим потери напряжения в процентах от шин ЦП до шин 0,38кВ каждой ТП. Так, для шин 10 будем иметь:
ΔU1-10 = 1,51 + 0,73 + 0,83 + 0,42 + 3,04 = 6,53%.
Результаты занесем в табл. 10.8.
По заданному отношению наименьшей нагрузки к наибольшей m = 0,25 найдем потери напряжения от шин ЦП до шин 0,38 кВ ТП в режиме наименьших нагрузок с использованием формулы:
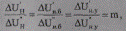
где
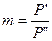
Здесь: Р’ , Р” — активная нагрузка в режиме наибольших и наименьших нагрузок; ΔU’н, ΔU’н.б, ΔU’н.у — соответственно потери напряжения от шин ЦП до шин 0,38 кВ ТП, ближайшего к ТП приемника и до наиболее удаленного от ТП приемника в режиме наименьших нагрузок; ΔU”н, ΔU”н.б, ΔU”н.у — то же, но в режиме наибольших нагрузок.
Таблица 10.8
Потери напряжения от шин ЦП до шин 0,38 кВ ТП
| Номер шин 0,38 кВ ТП | ΔU, %, в режиме | |
| наибольших нагрузок | наименьших нагрузок | |
| 3,95 | 0,99 | |
| 5,54 | 1,39 | |
| 5,58 | 1,4 | |
| 6,53 | 1,63 | |
| 5,67 | 1,42 |
Следовательно,
ΔU’н = ΔU”н m.
Так, для шин 3 (см. рис. 10.25) будем иметь:
ΔU’н = ΔU”н m = 3,95 • 0,25 = 0,99 %.
Результаты расчетов занесем в табл. 10.8.
4. Определение допустимых отклонений напряжения на шинах 0,38 кВ ТП.
Будем ориентироваться на то, что у ближайшего к ТП приемника отклонение напряжения может быть равно верхнему допустимому пределу δUб = +5 %, а у наиболее удаленного — нижнему допустимому пределу δUy = -5 %.
По условию задачи потеря напряжения в сети 0,38 кВ от шин ТП до наиболее удаленного приемника в режиме наибольших нагрузок равна ΔU”нн.у = 5 %, а до ближайшего приемника ΔU”нн.б = 0 %. Тогда в режиме наименьших нагрузок эта потеря напряжения составит:
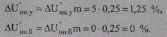
Допустимые отклонения напряжения на шинах 0,38 кВ ТП в режиме наибольших нагрузок вычислим по формулам (10.53):

Таким образом, в режиме наибольших нагрузок отклонение напряжения на шинах 0,38 кВ ТП должно находиться в пределах:
0% ≤ δU”ТП.доп ≤ +5 %.
 По формулам (10.54) аналогично найдем допустимые отклонения напряжения на шинах 0,38 кВ ТП в режиме наименьших нагрузок.
По формулам (10.54) аналогично найдем допустимые отклонения напряжения на шинах 0,38 кВ ТП в режиме наименьших нагрузок.
Таким образом, в режиме наименьших нагрузок отклонение напряжения на шинах 0,38 кВ ТП должно находиться в пределах:
-3,75%≤ δU”ТП.доп ≤ +5 %.
5. Выбор режима встречного регулирования напряжения на шинах 10 кВ ЦП.
Выберем следующий режим регулирования:
при наибольших нагрузках δU”цп = +5 %;
при наименьших нагрузках δU’цп =0 %;
Тогда, с учетом найденной зоны нечувствительности регулятора δUнч = 1,2%, по формулам для режима 4 из табл. 10.3 найдем пределы возможных отклонений напряжения на шинах ЦП в режиме наибольших нагрузок:
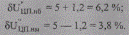
Аналогично по формулам для режима 4 из табл. 10.3 для режима наименьших нагрузок найдем: 
6. Выбор ответвлений трансформаторов ТП.
Найдем зону сети, в которой может быть выбрана наименьшая добавка напряжения на трансформаторах δUт.нм = 0,25 (соответствует ответвлению +5 % — табл. 10.4). Для этого вычислим соответствующие наибольшие потерн напряжения от ЦП до шин 0,38 кВ ТП. Для режима наибольших нагрузок по формулам (10.57) и (10.59) получим:
а) 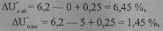
отсюда 1,45 ≤ ΔU”н≤ 6,45;
б) 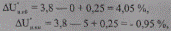
отсюда — 0,95 ≤ ΔU”н≤ 4,05.
Обобщая неравенства по пп. а) и б), получим, что при ответвлении +5 % потеря напряжения должна находиться в пределах:
1,45 ≤ ΔU”н≤ 4,05.
Этому условию удовлетворяет только трансформатор 2—3 (рис. 10.25), до шин 3 которого потеря напряжения равна 3,95 % (табл. 10.8):
1,45 ≤ 3,95 ≤ 4,05.
Проверим теперь выполнение требований (10.62) и (10.64) для режима наименьших нагрузок. Для этого произведем вычисления по формулам (10.61) и (10.63):
а) ΔU’н.нб= 1,2 — (-3,75) ± 0,25 = 5,20 %,
ΔU’н.нм = 1,2 —5+ 0,25 = -3,55%,
отсюда —3,55 ≤ ΔU’н.нм ≤ 5,20;
б) ΔU’н.нб = -1,2 — (-3,75) + 0,25 = 2,80 %,
ΔU’н.нм = -1,2 —5+0,25 = -5,95%,
отсюда —5,95 ≤ ΔU’н ≤ 2,80.
Обобщая неравенства по пп. а) и б), получим, что при ответвлении +5 % потеря напряжения должна находиться в пределах:
— 3,55 ≤ ΔU’н ≤ 2,80.
Этому условию трансформатор 2—3 также удовлетворяет, т. к. потеря напряжения до шин 3 составляет 0,99 % (табл. 10.8):
— 3,55 ≤ 0,99 ≤ 2,80.
Следовательно, по условию обоих режимов на трансформаторе 2—3 может быть выбрано ответвление +5 %.
Перейдем теперь к нахождению зоны сети, в которой может быть установлено ответвление трансформаторов +2,5 % с добавкой напряжения δUT = 2,70 % (табл. 10.4).
Для режима наибольших нагрузок по формулам (10.57) и (10.59) получим:
а) ΔU”н.нб = 6,2 — 0 + 2,7 = 8,9 %,
ΔU”н.нм = 6,2 — 5 + 2,7 = 3,9 %,
отсюда 3,9 ≤ ΔU”н ≤ 8,9;
б) ΔU”н.нб =3,8 — 0 + 2,7 = 6,5 %,
ΔU”н.нм =3,8 — 5 + 2,7 = 1,5 %,
отсюда 1,5 ≤ ΔU”н ≤ 6,5.
С учетом неравенств а) и б):
3,9≤ ΔU”н ≤ 6,5.
Этому условию удовлетворяют трансформаторы 5—6, 7—8, 11—12. По данным табл. 10.-8 для них соответственно имеем:
3,9 ≤5,54 ≤ 6,5,
3,9 ≤ 5,58 ≤ 6,5,
3,9 ≤ 5,67 ≤ 6,5.
Проверим требования режима наименьших нагрузок. По формулам (10.61) и (10.63) получим:
а) ΔU’н.нб = 1,2 — (-3,75) + 2,7= 7,65 %,
ΔU’н.нм = 1.2 — 5 + 2,7 = -1,1 %,
отсюда — 1,1 ≤ ΔU’н.нм ≤7,65;
б) ΔU’н.нб = -1,2 — (-3,75) + 2,7 = 5,2 5%,
ΔU’н.нм = -1,2 — 5 + 2,7 = -3,5 %,
отсюда —3,5 ≤ ΔU’н ≤5,25.
С учетом ограничений а) и б):
-1,1 ≤ ΔU’н.нм ≤5,25.
Трансформаторы 5—6, 7—8, 11—12 этим ограничениям также удовлетворяют, т. к. по данным табл. 10.8 для них соответственно имеем:
-1,1 ≤ 1,39 ≤ 5,25,
-1,1 ≤ 1,4 ≤ 5,25,
-1,1 ≤ 1,42 ≤5,25.
Следовательно, по условию обоих режимов на трансформаторах 5—б, 7—8 и 11—12 может быть установлено ответвление +2,5 %.
Далее найдем зону сети, соответствующую ответвлению трансформаторов 0 % с добавкой напряжения δUт = 5,26 % (табл. 10.4). Для этого проведем аналогичные расчеты.
Для режима наибольших нагрузок по формулам (10.57) и (10.59) получим:
а) ΔU”н.нб = 6,2 — 0 + 5,26 = 11,46 %,
ΔU”н.нм = 6,2 — 5 + 5,26 = 6,46 %,
отсюда 6,46 ≤ ΔU”н ≤ 11,46;
б) ΔU”н.нб = 3,8 — 0 + 5,26 = 9,06 %,
ΔU”н.нм = 3,8 — 5 + 5,26 = 4,06 %,
отсюда 4,06 ≤ ΔU”н ≤ 9,06.
С учетом неравенства по пп. а) и б):
6,46 ≤ ΔU”н ≤ 9,06.
Этому условию удовлетворяет трансформатор 9—10. Для него (табл. 10.8):
6,46 ≤ 6,53 ≤ 9,06
Для режима наименьших нагрузок:
а) ΔU’н.нб = 1,2 — (-3,75) + 5,26= 10,21 %,
ΔU’н.нм = 1,2 — 5 + 5,26 = 1,46 %,
отсюда 1,46 ≤ ΔU’н.нм ≤10,21;
б) ΔU’н.нб = -1,2— (-3,75)+ 5,26 = 7,81 %,
ΔU’н.нм = - 1,2 — 5 + 5,26 =-0,94 %,
отсюда — 0,94 ≤ ΔU’н≤7,81.
С учетом ограничений по пп. а) и б):
1,46 ≤ ΔU’н≤7,81.
Трансформатор 9—10 этому условию удовлетворяет (табл. 10.8):
1,46 ≤ 1,63 ≤ 7,81
Следовательно, на нем должно быть установлено ответвление 0 %.
Результаты выбора ответвлений трансформаторов сведены в табл. 10.9
Таблица 10.9
Выбранные ответвления трансформаторов
| Номер трансформатора | Выбранные ответвления, % |
| 2—3 | +5 |
| 5—6 | +2,5 |
| 7—8 | +2,5 |
| 9—10 | +0 |
| 11—12 | +2,5 |
ЗАДАЧА 10.2
На понижающей подстанции установлен трехфазный двухобмоточный трансформатор ТМН-4000/35 с регулированием напряжения под нагрузкой на стороне высшего напряжения, имеющий номинальные напряжения и диапазон регулирования
35 ± (6 x 1,5)% /6,3 кВ. По результатам расчета режимов сети на шинах низшего напряжения получены напряжения, приведенные к высшему напряжению: при наибольших нагрузках U’н.нб = 34 кВ, при наименьших нагрузках U’н.нм = 37 кВ, в послеаварийном режиме U’н.па = 32 кВ. За счет использования устройства РПН требуется обеспечить на шинах низшего напряжения режим стабилизации напряжения, т. е. неизменное напряжение во всех режимах сети Uн.ж.нб=Uн.ж.нм=Uн.ж.па=6,6 кВ
Решение
Рассчитаем напряжения ответвлений, соответствующие каждой ступени регулирования (табл. 10.10).
Таблица 10.10
Параметры регулирования напряжения трансформатора
с диапазоном регулирования ±(6 x 1,5) %
| Номер ответвления | 9 | ||||||||||||
| Добавка . напряжения, % | +9 | +7,5 | +6 | +4,5 | +3 | +1,5 | -1,5 | -3 | -4,5 | -6 | -7,5 | -9 | |
| Напряжение ответвления UВН.д, кВ | 38,2 | 37,6 | 37,1 | 36,6 | 36,1 | 35,5 | 34,5 | 34.0 | 33.4 | 32,9 | 32,4 | 31,9 |
По формулам (10.38) определим расчетные напряжения ответвлений обмотки высшего напряжения из условия обеспечения желаемого напряжения на шинах низшего напряжения, равного 6,6 кВ для всех рассматриваемых режимов:

На основе полученных расчетных напряжений ответвлений выберем из табл. 10.10 ближайшие стандартные напряжения для каждого из режимов:
UВН.д.нб = 32,4 кВ (добавка — 7,5 %),
UВН.д.нм = 35,5 кВ(+1,5%),
UВН.д.па = 31,9кВ(-9%).
По формулам (10.39) определим действительные напряжения на шинах 6 кВ во всех режимах:

Определим отклонения полученных действительных напряжений от желаемых
на шинах 6 кВ:

Результаты расчетов подставлены в табл. 10.11
Проведенные расчеты позволяют сделать следующие выводы: поскольку расчетное напряжение ответвления округлялось до ближайшего стандартного (большего или меньшего), то при достаточности имеющегося на трансформаторе диапазона регулирования и правильном выборе ответвлений отклонение действительного напряжения на шинах низшего напряжения от желаемого не должно превышать половины ступени регулирования, т. е. ±1,5/2 = ±0,75 %. Данное условие выполняется для нормальных режимов (наибольших и наименьших нагрузок). При этом в процессе регулирования напряжения в различных рабочих режимах сети от наибольших до наименьших нагрузок потребуется использование ответвлений от 12 (-7,5 %) до 6 (+1,5 %). Что касается рассмотренного послеаварийного режима, то для него выбрано крайнее ответвление 13 (-9 %). Тем не менее отклонение напряжения от желаемого оказалось
-4,24 %, т. е. больше половины ступени регулирования трансформатора. Следовательно, имеющегося диапазона регулирования устройства РПН трансформатора недостаточно для обеспечения желаемого напряжения в этом режиме. В подобных случаях требуется дополнительная проверка допустимости такого режима по условию работы потребителей либо применение дополнительных мер по регулированию напряжения.
Таблица 10.11
Результаты выбора ответвлений трансформатора
| Режим | Приведенное напряжение на шинах 6 кВ | Расчетное напряжение ответвления, кВ | Стандартное ответвление | Действительное напряжение на шинах 6 кВ | Отклонение действительного напряжения на шинах 6 кВ от желаемого,% | ||
| кВ | % | номер | |||||
| Наибольших нагрузок | 32,5 | 32,4 | -7,5 | 6,61 | +0,15 | ||
| Наименьших нагрузок | 35,3 | 35,5 | + 1,5 | 6,57 | -0,45 | ||
| Послеава-рийный | 30,5 | 31,9 | -9 | 6,32 | -4,24 |
ЗАДАЧА 10.3
На понижающей подстанции предполагается установить трехфазные двухобмоточные трансформаторы ТДН-10000/110 с регулированием напряжения под нагрузкой на стороне высшего напряжения, имеющие номинальные напряжения и диапазоны регулирования 115 ±(9 х 1,78)% /11 кВ. В результате выполненных проектных расчетов режимов питающей электрической сети получены напряжения на шинах 10 кВ, приведенные к напряжению 110 кВ: при наибольших нагрузках U’н.нб=10З кВ, при наименьших нагрузках, U’н.нм =114кВ, в послеаварийном режиме при наибольших нагрузках
U’н.па =100 кВ. Проверить достаточность диапазона регулирования устройства РПН для обеспечения встречного регулирования напряжения на шинах 10 кВ при следующих желаемых напряжениях: Uн.ж.нб = Uн.ж.па = 1,05Uном = 10,5 кВ, Uн.ж.нм= 1,0 Uном = 10,0 кВ.
Решение
Рассчитаем напряжения ответвлений для всех ступеней регулирования (табл. 10.12).
Таблица 10.12
Параметры регулирования напряжения трансформаторов
с диапазоном регулирования ±(9 х 1,78)%
| Номер ответвления | |||||||||||||||||||
| Добавка напряжения, % | +16,02 | +14,24 | +12,46 | +10,68 | +8,9 | +7,12 | +5,34 | +3,56 | +1,78 | -1,78 | -3,56 | -5,34 | -7,12 | -8,9 | -10,68 | -12,46 | -14,24 | -16,02 | |
| Напряжение ответвления Ubh.д, кВ | 133,4 | 131,4 | 129,3 | 127,3 | 125,2 | 123,2 | 121,1 | 119,1 | 117,0 | 115,0 | 113,0 | 110,9 | 108,9 | 106,8 | 104,8 | 102,7 | 100,7 | 98,6 | 96,6 |
По формуле (10.42) рассчитаем возможный наименьший коэффициент трансформации, соответствующий ответвлению 19 (-16,02 %):

Определим возможные максимальные напряжения на шинах 10 кВ при наибольших нагрузках и в послеаварийном режиме:

По формуле (10.43) найдем возможный наибольший коэффициент трансформации, соответствующий ответвлению 1 (+16,02 %):

Вычислим возможное минимальное напряжение на шинах 10 кВ при наименьших нагрузках:
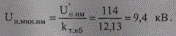
Таким образом, во всех режимах сети имеющегося диапазона регулирования трансформаторов будет достаточно для обеспечения заданного режима напряжений на шинах 10 кВ. Действительно, полученные возможные максимальные напряжения при наибольших нагрузках и в послеаварийном режиме больше желаемого (11,73 > 10,5 и 11,39 > 10,5). Следовательно, в условиях эксплуатации при переходе с крайнего ответвления —16,02 % на какое-то другое ответвление, с более высоким значением коэффициента трансформации, можно будет снизить полученные максимальные значения напряжений до желаемого. При наименьших нагрузках возможное минимальное напряжение получилось ниже желаемого (9,4 < 10,0). Отсюда следует, что в условиях эксплуатации оно также может быть повышено до желаемого путем перехода из крайнего ответвления +16,02 % в какое-то другое, соответствующее меньшему значению коэффициента трансформации.
На основании проведенных расчетов можно оценить запас, которым обладает располагаемый диапазон регулирования, путем сравнения полученных максимальных и минимального значений напряжений с желаемыми:
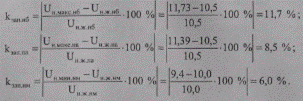
ЗАДАЧА 10.4
На понижающей подстанции установлен трехфазный трехобмоточный трансформатор ТДТН 16000/110 с регулированием напряжения под нагрузкой на стороне высшего напряжения и с переключением ответвлений без возбуждения на стороне среднего напряжения, имеющий номинальные напряжения и диапазоны регулирования
115±(9 х 1,78) % /38,5±(2 х 2,5) %/11 кВ.
По результатам электрических расчетов сети при наибольших и наименьших нагрузках, а также в послеаварийном режиме получены напряжения, приведенные к напряжению 110кВ:нашинах10кВ U’10нб = 105 кВ, U’10па = 102 кВ, U’10нм = 115 кВ; на шинах 35 кВ U’35нб = 107кВ, U’36па = 104 кВ, U’35нм = 117 кВ. Желаемые напряжения принять: на шинах 10 кВ исхода из требований встречного регулирования при наибольших нагрузках и в послеаварийном режиме Uж.нб=Uж.па=1,1Uном = 11 кВ, при наименьших нагрузках
Uж.нм = 1,0Uном; на шинах 35 кВ во всех режимах Uж = 36,5 кВ. Требуется выбрать ответвления на обмотках высшего и среднего напряжений.
Решение
Напряжение всех ответвлений обмотки 110 кВ приведены в табл. 10.12. Рассчитаем напряжения ответвлений обмотки 35 кВ (табл. 10.13).
Таблица 10.13
Параметры регулирования напряжения трансформатора
с диапазоном регулирования ±(2 х 2,5)%
| Номер ответвления | |||||
| Добавка напряжения, % | +5 | +2,5 | -2,5 | -5 | |
| Напряжение ответвления UСН.д , кВ | 40,43 | 39,46 | 38,5 | 37,54 | 36,58 |
Рассмотрим сначала трансформатор как двухобмоточный в направлении от обмотки высшего напряжения к обмотке низшего напряжения и в соответствии с желаемыми напряжениями на шинах 10 кВ выберем регулировочные ответвления при наибольших и наименьших нагрузках, а также в послеаварийном режиме. Для этого по формулам (10.38) определим желаемые напряжения ответвлений в каждом из режимов:
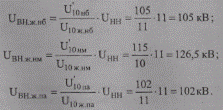
Из табл. 10.12 выберем ближайшие стандартные ответвления:
UВН.д.нб = 104,8 кВ (добавка — 8,9 %),
UВН.д.нм = 127,3 кВ (+8,9 %),
UВН.д.па = 102,7 кВ (—10,68 %).
При этих ответвлениях по формулам (10.39) найдем действительные напряжения на шинах 10 кВ:
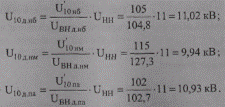
Отклонения напряжения от желаемых составят:
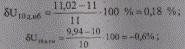
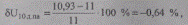
т. е. меньше половины ступени регулирования ±1,78/2 = ±0,89 %.
Таким образом, диапазон регулирования устройства РПН на обмотке 110 кВ позволяет во всех режимах создать заданные (желаемые) напряжения.
Рассмотрим теперь трехобмоточный трансформатор как двухобмоточный в направлении от обмотки высшего напряжения к обмотке среднего напряжения с целью выбора ответвления на обмотке 35 кВ. Поскольку на этой обмотке нет устройства РПН, приходится выбирать одно ответвление для всех режимов. Учитывая, что длительность послеаварийных режимов несоизмеримо меньше длительности нормальных режимов, а также то, что в сети 35 кВ по направлению передачи мощности потребителям будут встречаться трансформаторы 35/10(6) кВ с РПН, ориентироваться будем только на нормальные режимы наибольших и наименьших нагрузок. В качестве исходной информации примем уже выбранные ответвления для этих режимов на обмотке 110 кВ.
Желаемое напряжение ответвления на обмотке 35 кВ определим по формуле (10.40):

Из табл. 10.11 примем ближайшее ответвление UCH.д = 37,54 (-2,5 %).
По формулам (10.41) найдем действительные напряжения на шинах 35 кВ при выбранном ответвлении в различных режимах работы сети:
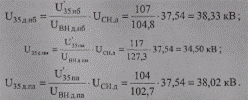
Полученные результаты показывают, что на шинах 35 кВ, так же как и на шинах 10 кВ, режим напряжений соответствует встречному регулированию, что благоприятно отразится на режиме напряжений в сети 35 кВ и далее по направлению передачи мощности в сети 10(6) кВ.
ЗАДАЧА 10.5
На понижающей подстанции установлен автотрансформатор с РПН на стороне среднего напряжения с номинальным напряжением вывода высшего напряжения UBH = 230 кВ и номинальным напряжением среднего ответвления на выводе среднего напряжения
UCH = 121 кВ. Ступень регулирования устройства РПН на автотрансформаторе составляет 2 %. По результатам расчета режима сети на шинах среднего напряжения получено напряжение U’с=206kB, приведенное к высшей стороне. Выбрать ответвление устройства РПН, если желаемое напряжение на шинах среднего напряжения UС.ж = 115 кВ.
Решение
По формуле(10.44) найдем желаемое напряжение ответвления

а по формулам (10.45) и (10.46) желаемую добавку напряжения
δUж = UСН.ж -UCH =128,39-121 = 7,4 кВ
или
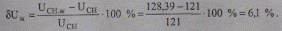
Ближайшая стандартная добавка δUд = 6 % или δUд = 0,06∙121= 7,26 кВ.
Действительное напряжение на шинах среднего напряжения без добавки и с добавкой δUд по формулам (10.47) и (10.48) будут равны:
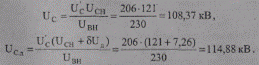
Изменение напряжения при введении добавки δUд = 7,26 кВ
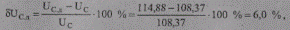
т. е. равно введенной добавке δUд = 6 %.
ЗАДАЧА 10.6
Задана электрическая сеть с номинальным напряжением 10 кВ и фиксированным коэффициентом трансформации 10/0,4 кВ трансформатора ТМ-1000/10 (рис. 10.26). Марка провода линии А70/11, длина линии 12,0 км. Мощность подключенная на стороне 0,38 кВ трансформатора при номинальном напряжении 10 кВ, Sном= Рном + jQном = 0,60 +j0,50 MBА и изменяется по статическим характеристикам
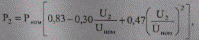
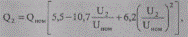
где Рном, Qном— нагрузки при номинальном напряжении.
Напряжение в точке питания U1 = 10,5 кВ. Требуется определить мощность батареи конденсаторов, которую необходимо установить на шинах 0,38 кВ подстанции для повышения напряжения в этой точке на 5%. Определить изменение потерь активной мощности в результате установки батареи конденсаторов.

Рис. 10.26. Схема сети
Решение
Из справочных данных найдем удельные параметры линии 10 кВ
Ro = 0,46 Ом/км, Хо = 0,341 Ом/км и рассчитаем сопротивления линии:
Rл = 0,46 • 12,0 = 5,52 Ом, Хл = 0,341 • 12,0 = 4,09 Ом.
Из справочных данных найдем сопротивления трансформатора
RT = 1,22 Ом, Хт = 5,36 Ом. Потерями холостого хода трансформатора будем пренебрегать.
Сопротивления от источника питания до точки подключения нагрузки равны:
R = Rл+ Rт = 5,52 + 1,22 = 6,74 Ом, X = Хл + Хт = 4,09 + 5,36 = 9,45 Ом.
Вычислим потерю напряжения от источника питания до точки подключения нагрузки:
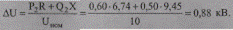
Найдем напряжение на шинах 0,38 кВ, приведенное к напряжению 10 кВ:
U'2 = U1 - ΔU = 10,5 - 0,88 кВ = 9,62 кВ.
Найдем напряжение на шинах 0,38 кВ с учетом заданного коэффициента трансформации:
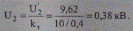
По условию задачи на шинах 0,38 кВ необходимо повысить напряжение на 5%, т. е. получить напряжение U2ж = 1,05U2 = 1,05∙0,38 = 0,40 кВ, что будет соответствовать приведенному напряжению
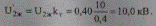
Для нахождения необходимой мощности батареи конденсаторов с целью повышения напряжения с U’2 =9,62 кВ до U’2ж = 10,0 кВ воспользуемся формулой (10.70):
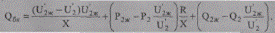
Предварительно найдем активные и реактивные мощности по статическим характеристикам: при U’2= 9,62 кВ
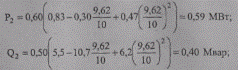
при U’2ж = 10,0 кВ, поскольку U’2ж оказалось равным Uном = 10 кВ, сразу можно записать Р2ж = 0,60 МВт, Q2ж = 0,50 Мвар.
Тогда
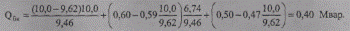
Требуемая номинальная мощность батареи конденсаторов будет равна
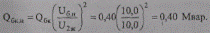
Найдем также по формуле (10.72) мощность батареи конденсаторов без учета статических характеристик:
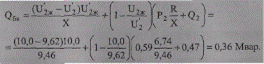
Таким образом, неучет изменения мощности нагрузки по статическим характеристикам привел к занижению мощности батареи конденсаторов на

Найдем потери активной мощности до и после установки батареи конденсаторов:
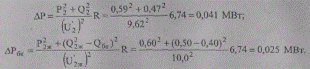
Таким образом, снижение потерь мощности составило:

ЗАДАЧА 10.7
Для линии электропередачи без потерь, работающей в режиме передачи натуральной мощности, определить напряжение U1 в начале линии при известном напряжении в конце линии U2 = 330 кВ. Линия выполнена сталеалюминиевыми проводами с расщепленными на два провода фазами и номинальным сечением проводов 240/32 мм2. Длину линии L принять изменяющейся от 200 до 1000 км.
Решение
Для заданных параметров линии (напряжения и площади сечения проводов) из справочников находим реактивное сопротивление х0 = 0,33 Ом/км и реактивную проводимость b0 = 3,38∙10-6 См/км.
Определим коэффициент изменения фазы волны для линии без потерь:

или в градусах

Из свойств натурального режима линии без потерь (параграф 10.4) следует, что модуль напряжения вдоль длины линии не изменяется. Следовательно,
|U1 |=U2 =330 кВ.
Угол сдвига между напряжением U1 и напряжением U2, направленным по вещественной оси, найдем по формуле (10.13):
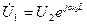
Здесь достаточно вычислить произведение α0L, называемое волновой длиной линии, при изменении длины линии в заданных пределах:
| L, км | |||||
| α0L, град | 12,1 | 24,2 | 36,3 | 48,4 | 60,5 |
ЗАДАЧА 10.8
Воздушная линия электропередачи номинальным напряжением Uном = 500 кВ длиной
L = 600 км выполнена маркой провода АС 400/51 с числом проводов в расщепленной фазе, равном 3. Напряжение в конце линии U2 = 500 кВ.
Определить реактивные мощности в конце и начале линии при следующих условиях:
1) Мощности в конце линии Р2=430 МВт, напряжение в начале линии U1 = 500 кВ,
2) Мощность в конце линии Р2=430 МВт, напряжение в начале линии U1 = 525 кВ.
3) Мощность в конце линии Р2 = 0, напряжение в начале линии U1 = 500 кВ.
4) Мощность в конце линии Р2=0, напряжение в начале линии U1 = 525 кВ.
5) Мощность в конце линии Р2 = 860 МВт, напряжение в начале линии U1 = 500 кВ.
6) Мощность в конце линии Р2 = 860 МВт, напряжение в начале линии U1 = 525 кВ.
7) Мощность в конце линии Р2 = 1290 МВт, напряжение в начале линии U1= 500 кВ.
8) Мощность в конце линии Р2 = 1290 МВт, напряжение в начале линии U1= 525 кВ.
Решение
Для заданных параметров линии (номинального напряжения и марки провода) из справочников найдем удельное реактивное сопротивление X0 = 306 Ом/км и реактивную проводимость bо = 3,62∙10-6 См/км.
Определим волновое сопротивление линии без потерь:
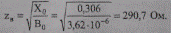
Вычислим натуральную мощность линии без потерь:
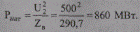
Найдем коэффициент изменения фазы волны и волновую длину линии:

Примем за базисные величины U6aз = U2 = 500 км, Р6aз = Рнат = 860 МВт.
Перейдем теперь к определению реактивной мощности в конце и начале линии при различных заданных условиях.
Условие 1. Р2 = 430 МВт, U1 = 500 кВ.
Мощность в конце линии в относительных единицах
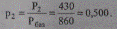
 Напряжение в начале линии в относительных единицах
Напряжение в начале линии в относительных единицах
Используя уравнение (10.16), найдем угол δ между векторами напряжений U1 и U2:
p2 sin(α0L) = U1*. sin δ;
0,5 sin 36,18 = sin δ, sin δ = 0,295, δ = 17,16°.
Поскольку в данном случае линия работает без перепада напряжения (U1 = U2), для вычисления реактивной мощности в конце линии воспользуемся формулой (10.18): 
В именованных единицах
Q2= q2Pбаз = 0,25∙860 = 215 Мвар.
Поскольку оказалось, что Q2 > 0, то, следовательно, мощность направлена в конец линии.
Аналогичным образом по формуле (10.20) найдем реактивную мощность в начале линии:
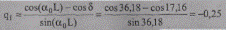
или
Q1= q1Pбаз =- 0,25∙860 = -215 Мвар.
Мощность Q1 < 0, следовательно, она направлена в сторону начала линии.
Таким образом, при передаче активной мощности меньше натуральной (430 < 860) и отсутствии перепада напряжений в линии возникает избыток зарядной мощности, который направлен в оба конца линии. Причем, поскольку U1 = U2, значения реактивной мощности в начале и конце линии оказываются одинаковыми.
Произведем также вычисления реактивных мощностей Q2 и Q1 по формулам, в которые непосредственно входит передаваемая активная мощность.
По формуле (10.25), соответствующей работе линии без перепада напряжений, имеем:
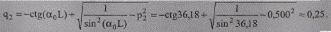
По формуле (10.24) для реактивной мощности в начале линии аналогично получим:
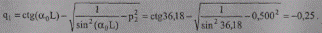
Таким образом, результат получился тот же самый:
Q2= q2Pнат = 0,25∙860 = 215 Мвар
Q1= q1Pнат = -0,25∙860 = -215 Мвар
Условие 2. Р2 = 430 МВт, U1 = 525 кВ.
В относительных единицах p2 = 0,500, 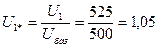 .
.
Составив уравнение (10.16), найдем угол δ:
0,5 sin 36,18 = 1,05 sin δ; sin δ = 0,281, δ = 16,32°.
Тогда по формуле (10.17)
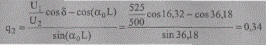
или
Q2 = q2Pнат = 0,34∙860 = 292,4 Мвар;
По формуле (10.19) вычислим реактивную мощность в начале линии:

или
Q1 = q1Pнат = -0,18∙860 = -154,8 Мвар.
Таким образом, направления реактивных мощностей в начале и конце линии сохранились прежними. Но из-за увеличения напряжения в начале линии значение потока реактивной
Дата добавления: 2021-02-19; просмотров: 1153;











