Теория гетерогенного горения углерода

В чистом виде гетерогенные реакции проявляются в крайне ограниченных областях температур, когда скорости этих реакций малы. Искажение закона реагирования вызывается появлением диффузионного торможения: диффузией кислорода и продуктов горения в объеме, окружающем горящую частицу и диффузией внутри массы кокса.

Физическая картина заключается в следующем: кислород подводится к внешней поверхности куска, на участках этой поверхности, где нет трещин, часть кислорода вступает в соединение с углеродом и выделяется определенное количество оксида и диоксида углерода.

При горении углеродной частицы можно выделить два основных процесса, определяющих скорость выгорания: диффузию кислорода к поверхности углеродной частицы и собственно скорость химического реагирования кислорода с углеродом [18].

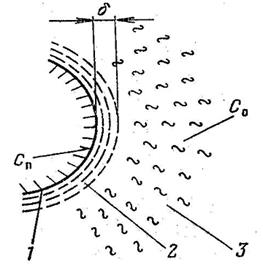
Рассмотрим общую теорию гетерогенного горения на примере горения одиночной углеродной сферической частицы, принимая следующие условия (рис. 4.1):

1. Концентрация кислорода по всей поверхности одинакова.

2. Реакция протекает на поверхности с образованием конечных продуктов, вторичное реагирование на поверхности и в газовом объеме отсутствует, т. е. идет только реакция (р1).

3. Имеет место реакция первого порядка по кислороду.

Поток кислорода, поглощаемый за счет химического реагирования, может быть рассчитан по формуле, кг/(м²×с),

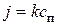, (4.7)

где k – константа скорости химического реагирования, м/с; с_п – концентрация кислорода на поверхности частицы кокса, кг/м³. С другой стороны, поток кислорода, доставляемый за счет диффузии к реагирующей поверхности, кг/(м²·с),

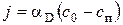, (4.8)

где a_D – коэффициент диффузионного массообмена, м/с; с₀ – концентрация кислорода в объеме газа, кг/м³.

Приравнивая потоки и исключая неизвестное значение концентрации углерода на поверхности с_п, получим выражение для константы обобщающей скорости взаимодействия кислорода с горящей углеродной частицей, включающей как диффузионное сопротивление, так и сопротивление химической реакции, кг/(м²·с),

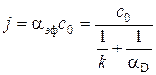, (4.9)

где α_эф – коэффициент реакционного газообмена, м/с.

В области низких температур скорость химических реакций мала (рис. 4.2) и во много раз меньше k << a_D ( 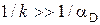) скорости, с которой кислород может быть доставлен диффузией к поверхности. Процесс ограничивается скоростью самого химического реагирования (j = kc₀). Поэтому эта область протекания реакции получила название кинетической. Концентрация кислорода на поверхности частицы равна концентрации кислорода в объеме газа с_п = с₀. При высоких температурах горение в кинетической области может наступить при больших скоростях потока и малых размерах частиц топлива.

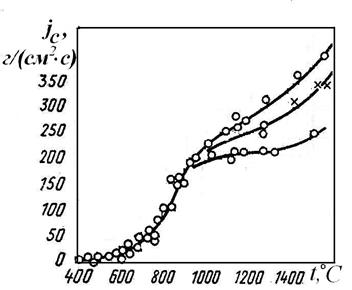
При высоких температурах скорость реакции, определяемая законом Аррениуса k=k₀·exp[-E/(RT)], настолько возрастает, что процесс горения начинает лимитироваться скоростью доставки кислорода к частице k >> a_D (1/k << 1/ά_D). Скорость реакции настолько велика, что доставляемый диффузией кислород мгновенно вступает в химическую реакцию с_п→0. Скорость горения в этом случае определяется скоростью диффузии кислорода к поверхности частицы (j = ά_Dc₀), режим горения называется диффузионным.

При сжигании твердого топлива в плотном либо псевдоожиженном слое, горение крупных частиц идет обычно в диффузионной области. При пылевидном сжигании относительная скорость между газом и топливной частицей невелика, при этом число Шервуда стремится к двум: 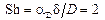. В данном выражении коэффициент молекулярной диффузии рассчитываю как коэффициент взаимодиффузии кислорода в азоте

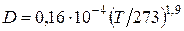. (4.10)

В данной области поток почти пропорционален температуре 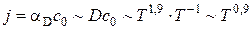. С уменьшением диаметра частицы, падает диффузионное сопротивление 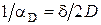, т. е. уменьшение диаметра пылевых частиц, позволяет повысить скорость их горения.