Расчет энтальпий и теплоемкостей
Как видно из приведенных уравнений, при тепловом расчете реактора необходимо обязательно знать энтальпии реакций, энтальпии фазовых переходов компонентов и теплоемкости компонентов.
Если отсутствует табличное значение, то энтальпию реакции можно определить по стандартным энтальпиям образования или сгорания компонентов в соответствии с законом Гесса. Для реакции
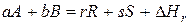
стандартная энтальпия реакции, рассчитанная по энтальпиям образования, равна
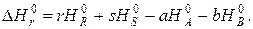
Соответственно по энтальпиям сгорания
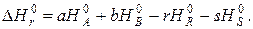
Значения стандартных энтальпий образования и сгорания можно найти в справочниках физико-химических величин. Значение энтальпии реакции при температуре реакции определяется уравнением
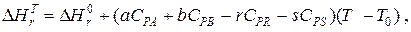
где СPi – мольная теплоемкость i-того компонента;
T0– “стандартная” температура;
T– расчетная температура.
Энтальпии компонентов можно рассчитать, используя энтальпии фазовых переходов и температурные зависимости теплоемкостей фаз. При условии задания уровня отсчета Tcобщая формула при этом будет иметь вид
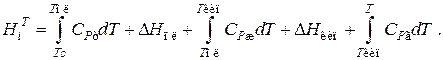
Индекс «пл» относится к температуре и энтальпии плавления, «кип» - к температуре и энтальпии кипения; «т», «ж» и «г» – соответственно к твердому телу, жидкости и газу. Температурные зависимости теплоемкостей для многих веществ можно найти в справочниках физико-химических величин, где они выражаются формулами:
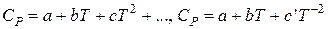
Если в данном температурном интервале в указанных уравнениях не окажется коэффициентов, то можно взять среднее значение теплоемкости, полученное из таблиц, или же рассчитанное по эмпирическим зависимостям.
Эмпирические зависимости расчета теплоемкости зависят от фазового состояния вещества. Так мольную теплоемкость металлов и других кристаллических веществ можно ориентировочно рассчитать по правилу Дюлонга и Пти, которое предполагает, что каждый атом соединения вносит в молекулу долю теплоемкости, равную примерно 26 Дж/(моль·К). Поэтому расчет удельной теплоемкости соединения можно провести по формуле
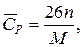
где n– число атомов в молекуле;
М – молекулярная масса соединения, кг/моль.
Теплоемкость многих твердых веществ – величина аддитивная и примерно равна сумме атомных теплоемкостей (правило Коппа):
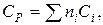
где ni – число атомов данного вида;
Сi – атомная теплоемкость, выбираемая из таблицы 9.7.
Вопрос о расчете теплоемкости некристаллических твердых соединений пока еще не решен, хотя с достаточно высокой ошибкой ее можно определить по правилу Коппа.
Мольная теплоемкость идеальных газов при обычной температуре и давлении выражается соотношениями, приведенными в табл. 9.8).
Таблица 9.7. Атомные составляющие теплоемкости твердых веществ
| Атом | Составляющая, Дж/(моль·К) | Атом | Составляющая, Дж/(моль·К) |
| C | 7,53 | F | 20,92 |
| H | 9,62 | P | 23,0 |
| O | 16,74 | Be | 15,9 |
| S | 22,59 | N | 11,3 |
| B | 11,72 | Другие атомы | 25,92-26,78 |
| Si | 20,08 |
Таблица 9.8. Мольные теплоемкости идеальных газов
| Вид газа | CV | CP | Вид газа | CV | CP |
| одноатомный | 1,5R | 2,5R | многоатомный | 3R | 4R |
| двухатомный | 2,5R | 3,5R |
Здесь CV и CP – теплоемкости при постоянном объеме и постоянном давлении, соответственно, а R – универсальная газовая постоянная, равная 8,314 Дж/(моль·К).
Ориентировочное значение удельной теплоемкости в Дж/(кг·К) можно получить из следующих формул:
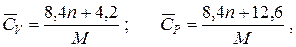
где n – число атомов в молекуле;
M –молярная масса соединения, кг/моль.
Зависимость теплоемкости газов и парогазовых смесей от давления и температуры ориентировочно определяется по формуле
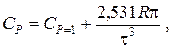
где CP=1 – теплоемкость при атмосферном давлении, Дж/(моль·К);
p- приведенное избыточное давление газа, 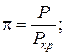
P – избыточное давление газа, Па;
Pкр – критическое давление газа, Па;
t - приведенная температура газа, 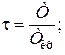
Т – температура газа, К;
Ткр – критическая температура газа.
Теплоемкость газовых и парогазовых смесей можно приближенно определить из выражения

гдеxi – молярная или объемная доля компонента в смеси.
Пример 9.7. Определить теплоемкость азота при температуре 50 ºС и абсолютном давлении 20 МПа.
Решение: По литературным данным для азота критическая температура равна 125,9 К, критическое давление – 3,285 МПа, молярная масса – 0,028 кг/моль. Определим изобарную теплоемкость при обычной температуре и атмосферном давлении

Приведенная температура равна 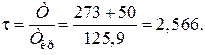
Приведенное избыточное давление 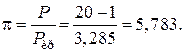
Тогда 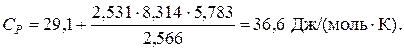
Или по удельной теплоемкости
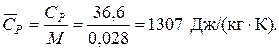
Удельная теплоемкость подавляющего большинства жидкостей лежит в пределах 1600-2400 Дж/(моль·К), для большинства углеводородов этот параметр примерно равен 2100 Дж/(моль·К).
Ориентировочную оценку мольной теплоемкости жидкостей можно провести, используя правило Коппа, которое применимо для температуры
20 ºС:
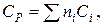
где ni– число атомов данного вида;
Ci – атомная теплоемкость, выбираемая из табл. 9.9.
Мольную теплоемкость жидкостей при 20 ºС можно вычислить по методу Джонсона-Хуанга:
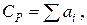
где ai – атомная или групповая составляющие (см. табл. 9.9).
Таблица 9.9. Атомные составляющие теплоемкости жидкостей
| Атом | Составляющая,Дж/(моль·К) | Атом | Составляющая,Дж/(моль·К) |
| C | 11,72 | Si | 24,27 |
| H | 17,99 | F | 29,29 |
| O | 25,10 | P | 29,29 |
| S | 30,96 | Другие атомы | 33,5 |
| B | 19,66 |
Вторая формула Джонсона-Хуанга дает возможность получить температурную зависимость теплоемкости
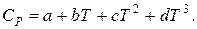
Коэффициенты a, b, c и d представлены в табл. 9.10.
Пример 9.8. Вычислить по методу Джонсона-Хуанга теплоемкость бензола (С6Н6) при 20 ºС.
Решение: Бензол можно представить состоящим из шести групп =СН¾, тогда СР=6·22,6=135,6 Дж/(моль·К). Опытное табличное значение 136,2 Дж/(моль·К).
Таблица 9.10. Атомные и групповые составляющие метода Джонсона-Хуанга
| Атом, группа | ai, Дж/(моль·К) | Атом, группа | ai, Дж/(моль·К) |
| H (в муравьиной кислоте и ее эфирах) | 14,86 | ¾CH= | 46,05 |
| ¾CH3 | 41,44 | ¾NH2 | 63,63 |
| ¾CH2- | 26,37 | ¾Cl | 36,00 |
| =CH¾ | 22,60 | ¾Br | 15,49 |
| ¾COOH | 79,95 | ¾NO2 | 64,05 |
| ¾COO— (сложные эфиры) | 60,70 | ¾O— (простые эфиры) | 35,16 |
| >C=O | 61,53 | ¾S¾ | 44,37 |
| ¾CºN | 58,19 | ¾C6H5 | 127,67 |
Важной характеристикой при тепловом расчете реакторов может являться энтальпия испарения. В том случае, если нельзя найти ее табличное значение, ее можно рассчитать. Наиболее простым, но и не вполне точным методом является правило Трутона:
Lисп.к=87,9Тк,
где Lисп.к– энтальпия испарения при температуре кипения, Дж/моль;
Тк– температура кипения, К.
Таблица 9.11. Расчет теплоемкости по методу Джонсона-Хуанга
| Группа | a | b·102 | c·104 | d·106 |
| ¾CH3 | 1.787 | 9.138 | -0.3612 | 0.00465 |
| ¾CH2¾ | -0.779 | 9.389 | -0.5287 | 0.01147 |
| =CH2 | 2.771 | 7.409 | -0.3659 | 0.00699 |
| =CH¾ | -1.000 | 6.961 | -0.4420 | 0.01088 |
| C6H5¾ | -31.71 | 46.08 | -3.0516 | 0.07539 |
| ºCH | 8.443 | 5.860 | -0.4843 | 0.01473 |
| ¾CH= | -21.987 | 16.27 | -1.8418 | 0.06367 |
| ½ ¾CH ½ | -8.129 | 11.85 | -0.9548 | 0.02767 |
| ¾CH2—C6H5 | -8.945 | 10.35 | -0.5002 | 0.00829 |
| ¾CH2—C5H4 | -9.703 | 10.34 | -0.5417 | 0.01076 |
| ½ ¾C¾ ½ | -19.49 | 15.41 | -1.4865 | 0.04111 |
| >C= | -0.224 | 5.618 | -0.4266 | 0.01143 |
Более точным является метод Джиаколоне:
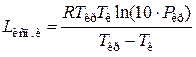 ,
,
где – Ткр и Ркр –критические температура (К) и давление (МПа).
Энтальпию плавления можно приближенно определить по формуле
Lпл=56,5Тпл,
где Lпл – энтальпия плавления, Дж/моль;
Тпл – температура плавления, К.
Для органических соединений соотношение между энтальпиями испарения и плавления имеет вид Lпл » 0,356Lисп.к.
9.6. Расчет реактора
периодического действия
В общем случае технологический процесс в реакторе периодического действия протекает в несколько стадий. Если предполагается химическую реакцию проводить в изотермическом режиме, то условно можно весь процесс разделить на следующие этапы:
1. Подготовка реактора к загрузке реагентов.
2. Загрузка реагентов в реактор.
3. Доведение условий проведения реакции (температуры, давления и т. д.) до заданных.
4. Проведение химического процесса до заданной глубины превращения.
5. Доведение условий выгрузки продуктов реакции (температуры, давления и т. д.) до заданных.
6. Подготовка реактора к выгрузке продуктов реакции.
7. Выгрузка продуктов реакции из реактора.
График такого условного технологического процесса в реакторе периодического действия можно проиллюстрировать рис. 9.3.
При поверочном расчете реактора должны быть известны времена проведения всех стадий, начальные и конечные температуры в реакторе, достигаемые степени превращения и, естественно, масса загружаемых компонентов. Задачей такого расчета является определение теплонапряженности каждой стадии с дальнейшим расчетом достаточности поверхности теплопередачи для нормального ведения процесса.
На основе известных данных, уравнений реакций и кинетических закономерностей для каждой стадии составляется система материальных и тепловых балансов, из которых рассчитывается количество передаваемого тепла. По расходу этого тепла можно рассчитать либо максимально потребную поверхность теплопередачи, либо расход теплоносителя, либо его начальную и конечную температуру.

|
| Рис. 9.3. К тепловому расчету реактора периодического действия |
Рассмотрим на примере графика на рис. 9.3 порядок расчета многостадийного периодически действующего реактора для простой реакции первого порядка А=В. Допустим, что известны: времена протекания стадий t1-t7, температуры Т1–Т4 и степени превращения ключевого компонента А в конце третьей стадии – ХА1, в конце четвертой стадии – ХА2 и в конце пятой стадии – ХА3. Кроме того, известны все физико-химические свойства компонентов и энтальпия реакции DН. Зависимость константы скорости реакции от температуры выражается известной функцией k=k(T).
1-ая стадия. Эта стадия технологического расчета не требует, так как основной ее параметр – время протекания – определен расчетным заданием.
2-ая стадия. Здесь возможно снижение или увеличение температуры загружаемых реагентов за счет теплообмена с материалом реактора. Запишем уравнение теплового баланса
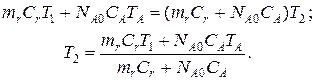
Здесь mr и Cr – масса и теплоемкость материала реактора;
NA0 и CA – число молей компонента А и его теплоемкость.
Таким образом, определена начальная температура в реакторе Т2.
3-я стадия. На этой стадии происходит доведение температуры процесса до заданной - Т3. Допустим, что реакция эндотермична (DН – положительна) и требуется нагрев реакционной смеси. Из уравнения баланса тепла определяется количество тепла, необходимое для нагревания реакционной смеси
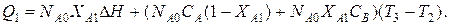
Среднее значение теплового потока третьей стадии (Вт) выразится уравнением
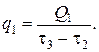
Имея значение теплового потока, можно определить расход теплоносителя. Определяя известными методами коэффициент теплопередачи по заданным температурам теплоносителя и реакционной смеси, можно найти поверхность теплопередачи на рассматриваемом этапе технологического процесса:
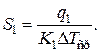
4-ая стадия. Здесь протекает изотермический процесс при постоянном коэффициенте теплопередачи. В этом случае уравнение баланса тепла будет
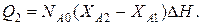
Значение теплового потока выразится также формулой
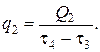
Требуемая поверхность теплообмена в этом случае будет равна
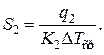
5-ая стадия. На этом этапе происходит охлаждение реакционной смеси с затуханием химической реакции. Уравнение баланса тогда выразится формулой
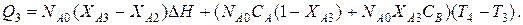
Среднее значение теплового потока выразится также формулой

Требуемая поверхность теплообмена в этом случае будет равна
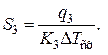
6-ая и 7-ая стадии. Эти стадии расчету не подлежат, так как их основной параметр – время протекания – задан.
В качестве расчетной, принимают наибольшую поверхность теплообмена из полученных.
Если в реакторе на какой-либо стадии происходит плавление, кристаллизация, испарение или конденсация компонентов реакции, то энтальпии этих процессов должны быть учтены соответствующими слагаемыми в уравнениях теплового баланса.
При проектном расчете реактора необходимо иметь данные о годовой производительности установки, о стехиометрических и кинетических закономерностях процесса и о выходе целевого продукта реакции. Разбивка процесса на стадии и определение времени их протекания входит в задачу такого расчета. Основным результатом проектного расчета является определение основных конструктивных размеров реактора и его теплопередающих поверхностей.
Сложность проектного расчета заключается в зависимости конструктивных размеров аппарата и времен проведения процесса на стадиях 3, 4 и 5. Здесь приходится составлять систему материальных и тепловых балансов совместно для всех трех стадий и решать ее любыми численными методами (чаще всего методом последовательных приближений).
9.7. Степень термодинамического
совершенства технологических процессов
Применение прогрессивных энергосберегающих технологических схем и повышение энерготехнологической эффективности оборудования являются важными задачами химического производства.
При разработке высокоэффективных и малоэнергоемких технологий и оборудования большое значение имеют вопросы использования вторичных ресурсов и утилизации побочных энергоресурсов, под которыми понимают неиспользованный в технологическом процессе энергетический потенциал всех продуктов и отходов. Например, применение котлов-утилизаторов, которые позволяют использовать теплоту отходящих газов для производства пара или подогрева воды. Другим примером может служить использование теплоты, полученной за счет охлаждения химически очищенной водой элементов, расположенных в высокотемпературной зоне (например, печи). При этом охлаждаемые поверхности используются в качестве испарителей для получения водяного пара.
Первым шагом по пути модернизации любого процесса является анализ степени его совершенства и сопоставление его с другими вариантами процессов, предназначенных для одной цели.
Объективная оценка степени энергетического совершенства любого технологического процесса и агрегата может быть сделана лишь на основе термодинамического анализа.
Простейшим из них является энергетический метод – на основе первого закона термодинамики. Например, энергетический баланс тепловой установки (рис. 9.4) можно записать следующим образом: Q1=Q2+Qn,
где – Qn – это энергия, которая не используется в технологической системе.
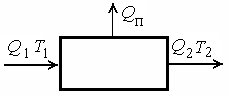
|
| Рис. 9.4 |
Если предположить, что
Qn=0, а Q2=Q1,
то тепловой (энергетический) коэффициент полезного действия (КПД)
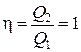
Известно, что любой процесс, независимо от того, как он будет технологически оформлен, при правильном подсчете всех энергетических потоков имеет коэффициент полезного действия близкий к единице, и нет смысла в его совершенствовании. Кроме того, из данного уравнения энергетического баланса неясно, используется энергия Q2 где-то или нет.
Таким образом, энергетический баланс не дает полной информации, прежде всего о качественных изменениях, происходящих в системе. При составлении энергетического баланса невозможно объективно учесть вторичные энергоресурсы (ВЭР). Если ВЭР вычесть из суммы общих энергозатрат, то расход энергозатрат будет заниженным, а если их вообще не учитывать, то энергозатраты получаются сильно завышенными. Кроме того, при комплексном производстве невозможно правильно распределить затраты энергии на различные виды продукции.
Для оценки степени совершенства технологического процесса следует использовать энергетический анализ на основе второго закона термодинамики и степень совершенства процесса понимать как степень его обратимости.
В обратимом процессе сумма энергии потоков, подведенных к системе, равна сумме потоков энергии, отведенных от нее:
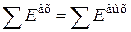 ,
,
тогда коэффициент полезного действия в обратимом процессе равен

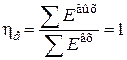 .
.
В любом реальном процессе вследствие его необратимости
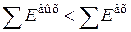
и тогда
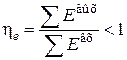 .
.
Таким образом, в реальных процессах эксергетический коэффициент полезного действия (hе) всегда меньше единицы, на величину эксергетических потерь (DD)
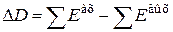
 .
.
По существу, 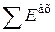 является суммой всех энергетических затрат на осуществление данного процесса, а
является суммой всех энергетических затрат на осуществление данного процесса, а 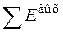 - обобщенная валовая производительность агрегата.
- обобщенная валовая производительность агрегата.
Таким образом, hе отражает степень совершенства любого процесса: будь то производство энергии или другой технологический процесс.
В табл. 9.12 приведены значения энергетических (тепловых) и эксергетических коэффициентов полезного действия электрических машин и тепловых установок.
Таблица 9.12. Сравнение энергетических и эксергетических КПД
| Вид установки (машины) | Энергетический, hq | Эксергетический, hе |
| Электродвигатель | 0,85-0,95 | 0,90 |
| Электрогенератор | 0,96-0,99 | 0,98 |
| Паровой котел | 0,88-0,92 | 0,49 |
| Газовая печь | 0,60-0,85 | 0,13 |
| Печь на жидком топливе | 0,45-0,70 | 0,11 |
Из табл. 9.12 видно, что менее совершенными являются тепловые процессы, для которых значения эксергетических коэффициентов полезного действия в 2-5 раз ниже энергетических коэффициентов полезного действия.
Для того, чтобы составить эксергетический баланс типового химико-технологического процесса, необходимо перечислить основные виды эксергии:
- эксергия теплового процесса [Eq];
- эксергия вещества [Eв];
- эксергия химическая [Ex];
- эксергия нулевая [E0].
Тогда эксергетический баланс можно изобразить так, как это показано на рис. 9.5.
Рис. 9.5
Для такой системы уравнение эксергетического баланса можно записать в следующем виде:
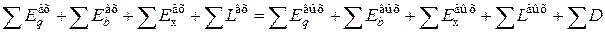 .
.
В общем виде эксергетический коэффициент полезного действия равен
 .
.
Если 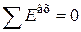 , то
, то 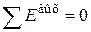 , тогда уравнение эксергетического баланса запишется следующим образом:
, тогда уравнение эксергетического баланса запишется следующим образом:
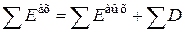 ;
;
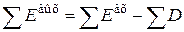 ;
;
и 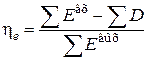 .
.
Для приближенной оценки степени совершенства процессов можно использовать эксергетические потери.
Эксергетические потери делятся на внутренние и внешние:
- внутренние потери эксергии связаны с необратимостью процессов, протекающих внутри системы ( потери при дросселировании, трении, при наличии гидравлических сопротивлений);
- внешние потери эксергии связаны с условиями сопряжения системы с окружающей средой (выброс продуктов производства в окружающую среду, плохая изоляция системы и т. д.).
Внутренние потери чаще всего связаны с несовершенством машин и аппаратов, а внешние – с несоответствием между процессом и условиями его проведения.
Практическое значение такого разделения эксергетических потерь связано с различными способами уменьшения внутренних и внешних потерь.
Ниже приводится пример использования эксергетических потерь для оценки степени совершенства типового технологического процесса и его технологического оформления.
Пример 9.8.Условия проведения процесса в реакторе:
- сырье поступает в реактор при температуре t1=195 °С;
- продукты реакции выходят из реактора с температурой t2=185 °С;
- исходная температура сырья tисх=30 °С;
- теплоемкость сырья и продуктов реакции не меняется;
- тепловыми потерями в окружающую среду пренебрегаем;
- конечная температура продуктов реакции tкон=30 °С;
- температура сухого насыщенного пара tп=200 °С;
- процесс конденсации пара изотермический;
- количество тепла, необходимое для нагревания сырья от tисх до t1, равно 1 МДж;
- температура в котле утилизаторе tку=150 °С;
- потери эксергии в реакторе для всех схем одинаковы.
Решение: Так как потери эксергии в реакторе одинаковы, для оценки технологических схем достаточно определить потери эксергии за счет теплообмена в теплообменниках (DDT).
Расчет производится по формулам:
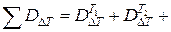 ...;
...;

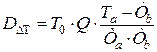 ;
;
где Т0=298К;
Q – теплота, передаваемая от одного теплоносителя со средней температурой Ta к другому – со средней температурой Тб.
Теплота, необходимая для нагревания сырья, по условию равна
1МДж, теплоту, необходимую для охлаждения продуктов реакции от t2 до tкон, определяют по формуле
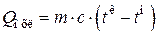
где tн и tк - температуры теплоносителя на входе и выходе.
Так как теплоемкость (с) и масса (m) продуктов реакции равны теплоемкости и массе сырья, то произведение 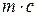 можно определить по формуле
можно определить по формуле
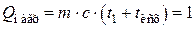 откуда
откуда
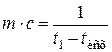 , МДж/К.
, МДж/К.
Тогда количество теплоты на охлаждение равно
 МДж.
МДж.
Отметим, что сумма 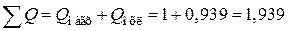 МДж сохраняется постоянной во всех схемах.
МДж сохраняется постоянной во всех схемах.
Рассчитаем потери эксергии для первого варианта технологической схемы (рис. 9.6).
Потери эксергии в теплообменнике Т1 равны
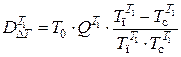 ,
,
где 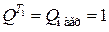 МДж,
МДж,
средняя температура сырья равна
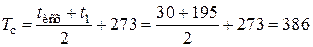 К.
К.
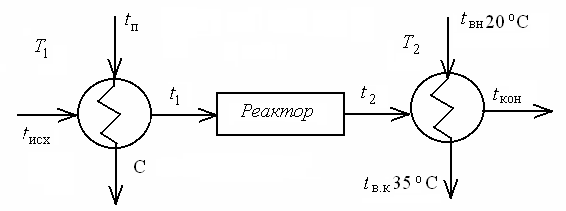
|
| Рис. 9.6. Технологическая схема 1: T1 и Т2 – теплообменники |
Температура греющего пара не меняется, так как идет процесс конденсации пара
Тп=tп+273=200+273=473K;
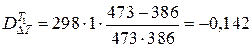 МДж.
МДж.
В теплообменнике Т2
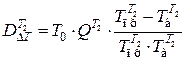 ,
,
где 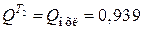 МДж.
МДж.
Средняя температура продуктов реакции равна
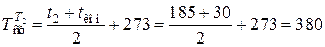 К,
К,
а средняя температура воды
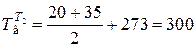 К;
К;
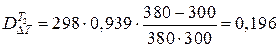 МДж.
МДж.
Общие потери эксергии по первой схеме равняются:
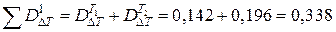 МДж.
МДж.
Потери эксергии, отнесенные к сумме теплот на нагревание и охлаждение продуктов реакции (Dе) сырья, равны
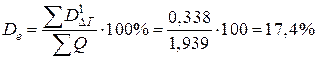 .
.
Второй вариант технологической схемы включает котел-утилизатор и возможность использования теплоты конденсата водяного пара для подогрева исходного сырья (рис. 9.7).
Для расчета потерь эксергии необходимо определить количество передаваемой в каждом теплообменнике теплоты и температуры t3 и t4.
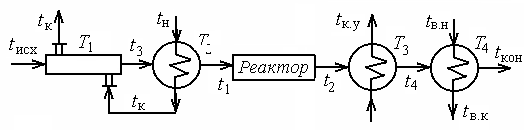
|
| Рис. 9.7. Технологическая схема 2 |
Как следует из условий, общее количество теплоты, передаваемой в теплообменниках Т1 и Т2, равно 1 МДж. Принимаем, что распределение теплоты по этим теплообменникам прямо пропорционально количеству теплоты, отдаваемой килограммом конденсирующегося пара при его охлаждении от (tn) до температуры конденсата на выходе из теплообменника
Т1-(tк), т. е. 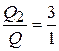 .
.
Считая, что теплоносители в теплообменнике Т1 движутся противотоком, примем tк на десять градусов выше, чем температура другого теплоносителя на входе (tисх).
Tк=tисх+10=30+10=40 °С.
Для 1 кг пара теплота конденсации, по справочным данным, составляет при 200 °С - 1938 кДж/кг; теплота охлаждения конденсата
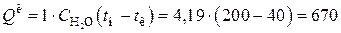 кДж/кг.
кДж/кг.
Отсюда, количество теплоты, передаваемое в каждом теплообменнике, составит:
в теплообменнике Т1 - 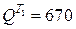 кДж/кг;
кДж/кг;
в теплообменнике T2 - 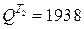 кДж/кг.
кДж/кг.
Определяем температуру t3 из уравнения:
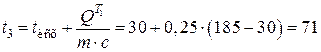 °С.
°С.
Потери эксергии в теплообменнике Т1 определяем из уравнения:
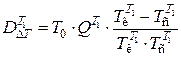 ,
,
где 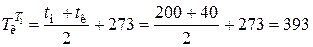 К - усредненная температура конденсата;
К - усредненная температура конденсата;
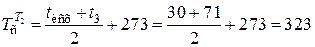 К - усредненная температура сырья.
К - усредненная температура сырья.
Отсюда следует, что
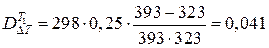 МДж.
МДж.
Потери эксергии в теплообменнике Т2
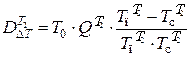 ,
,
где 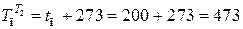 К;
К;
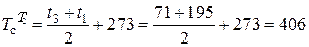 К.
К.
Отсюда следует, что
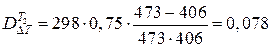 МДж.
МДж.
Примем температуру t4 на 20 оС выше, чем температура воды в котле-утилизаторе, т. е. t4=tку+20=170 °С. Тогда количество теплоты, передаваемое в каждом теплообменнике Т3 и Т4, будет равно соответственно
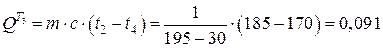 МДж;
МДж;
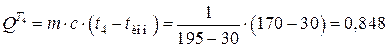 МДж.
МДж.
Проверяем общую сумму теплот:
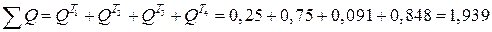 МДж.
МДж.
Потери эксергии в теплообменнике Т3
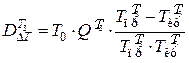 ,
,
где
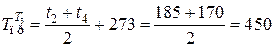 К;
К;
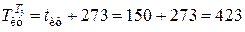 К;
К;
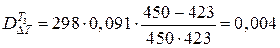 МДж
МДж
Потери эксергии в теплообменнике Т4:
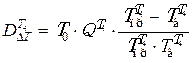 ,
,
где
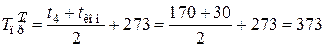 К;
К;
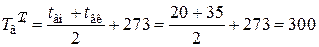 К;
К;
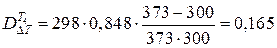 МДж.
МДж.
Общая сумма потерь эксергии во второй сумме равна
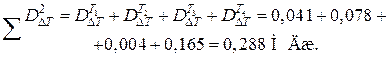
Отношение потерь эксергии во второй схеме
|
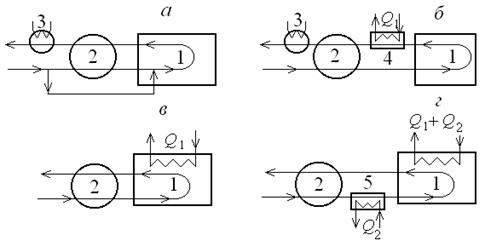
| Рис. 9.8. Схемы использования тепла реакций: а – с холодным байпасом; б – с отводом тепла реакции в выносном аппарате; в – с отводом тепла непосредственно из реактора; г – с предварительным подогревом реактивов; 1 – реактор; 2 – теплообменник; 3 – холодильник; 4 – аппарат для использования тепла реакции; 5 – подогреватель реагентов |
Как показали расчеты, более совершенной с точки зрения использования энергии является второй вариант технологической схемы.
Необходимо отметить, что реальные схемы утилизации тепла сложнее и могут быть многоступенчатыми.
Существует три группы методов экономии энергетических ресурсов:
1. Методы, связанные с увеличением поверхностей аппарата, времени протекания реакции, использованием более активных катализаторов, что позволяет приблизиться к равновесному состоянию на выходе из аппарата.
2. Методы, основанные на изменении технологического режима и не связанные с изменением технологической схемы, что может привести к увеличению габаритов аппарата.
3. Методы, требующие наряду с приемами, изложенными выше, изменение технологической схемы.
При разработке технологической схемы необходимо производить совместный анализ энергетического и эксергетического балансов с целью установления уровня возврата и возможности использования электрической, тепловой и механической энергии с существенным сокращением потребляемой извне энергии. Кроме того, при выборе относительного варианта технологической схемы должны быть учтены технико-экономические показатели.
Г л а в а 10
__________________________________________________________________
Дата добавления: 2021-02-19; просмотров: 1038;











