Неоднородное уширение линии излучения.

Кроме описанных причин уширения линии возможны такие, при которых линии излучения активных центров не совпадают друг с другом. В результате каждая частица или группа частиц излучает в пределах не всей наблюдаемой линии, и уширение в таком случае называется неоднородным.

Классическим примером неоднородного уширения является допплеровское уширение, характерное для газов при малых давлениях и высоких частотах. Частицы газа находятся в тепловом движении. Из-за этого каждая частица излучает смещенную в соответствии с эффектом Допплера частоту. Поскольку направления и величины скоростей движения частиц могут различаться, то линии испускаемого ими излучения оказываются сдвинутыми друг относительно друга. Обозначим p(u) — распределение частиц по скоростям. Соответствующий форм-фактор доплеровской линии q_д(n) можно простым соотношением связать с p(u):

q_д(n) dn = p(u) du (4.9),

учитывающим то, что суммарная форма линии определяется распределением частиц по скоростям. Прочими смещениями частоты в данном случае пренебрегаем. Тогда (4.9) отражает тот факт, что число частиц, имеющих скорости в интервале du, ответственно за «кусок» форм–фактора в интервале dn . Наблюдаемая частота, в соответствии с эффектом Допплера, равна:

n = n₀ ´ (u/c) (4.10)

Отсюда:

q_д(n) = (c/n₀) ´ p (c [n – n₀]/ n₀) (4.11)

Если принять максвелловское распределение по скоростям:

p(u) =( 1/u₀ ´ ) exp[(– u/u₀)²] (4.12),

то выражение для q_д(n) примет вид кривой Гаусса:

q_д(n) = (1/Dn_T ´ ) exp [–(n –n₀)/Dn_T] ² (4.13),

где

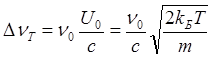(4.14)

В (4.14) использовано выражение для средней тепловой скорости частиц газа, известное из молекулярной физики:

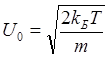(4.15)

где k_Б — постоянная Больцмана, Т — абсолютная температура, m — масса частицы газа.

Вообще говоря, при выводе формулы (4.13) допущены определенные нестрогости. Так, игнорируются все прочие механизмы уширения, а ведь естественным уширением пренебрегать мы не вправе. Поэтому необходимо помнить, что проведенные рассуждения, итогом которых является формула (4.13), справедливы при условии малости естественной ширины линии по сравнению с доплеровскими сдвигами.

Кроме того, вывод (4.13) основан на максвелловском распределении по скоростям, полученном в предположении о термодинамическом равновесии в системе, да не просто равновесии, а детальном равновесии, реализующемся при полной равновероятности всех возможных отклонений от равновесного состояния. Вроде бы налицо противоречие с необходимостью нарушения термодинамического равновесия в активной среде. Но это противоречие не носит принципиального характера. Нарушение термодинамического равновесия, распространяющееся на два рабочих уровня, очень мало сказывается на тепловом равновесии системы в целом. Во всяком случае, на распределение частиц по скоростям его влиянием можно пренебречь. Поэтому оценки уширения линии, получаемые из максвелловского распределения по скоростям, оказываются в очень хорошем согласии с экспериментом.

Формула (4.13), также записана в нормированном виде, т.е. с учетом выполнения требования нормировки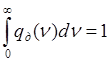

Полезно изобразить гауссову и лоренцеву формы линии на одном чертеже (рисунок 4.2):

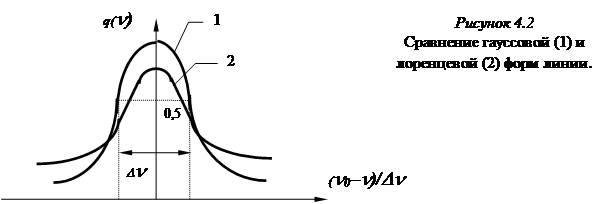Гауссова кривая симметрична, как и лоренцева, относительно центральной частоты n₀ , но ведет себя существенно отличным от лоренцевой образом. Около n₀ гауссова кривая более полога, зато на крыльях спадает существенно более круто. При удалении от n₀ на Dn_Т интенсивность спадает в е раз.

Если, как и для лоренцевой кривой, определить ширину линии Dn_D как расстояние по частоте между такими точками отстройки от n₀ , в которых интенсивность падает в 2 раза, то легко получить, что эта ширина равна:

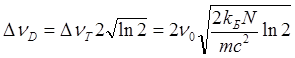(4.16)

На рисунке 4.2 гауссова и лоренцева кривые изображены для одинаковой
ширины линии излучения Dn =Dn_Л =Dn_D. В реальных системах неоднородное уширение добавляется к однородному.

Для оценки доплеровской ширины удобно пользоваться формулой:

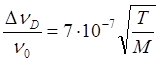(4.17)

где Т — температура, М — относительная молекулярная масса. В видимом диапазоне при не слишком высоких температурах Dn_D составляет (0,8…1,5) ГГц. Для грубых численных оценок в условиях тлеющего газового разряда (реализуемого для возбуждения в большинстве газовых лазеров) можно брать Dn_D /n₀ @ (2 – 3)´10^–6 [1].

Сопоставим полученные оценки с однородным уширением.

Как уже говорилось, в реальных условиях ширина лоренцевой кривой определяется столкновениями частиц, а естественным уширением можно при этом пренебречь. В классическом приближении (возбужденная частица рассматривается как гармонический осциллятор, возмущенный внешним полем) столкновительное уширение линии наиболее убедительно описывается случайными изменениями фазы колебаний осциллятора при взаимодействии с внешним полем. Среднее время свободного пробега осциллятора между двумя фазосбивающими столкновениями называется средним временем жизни частиц газа по отношению к таким столкновениям (при сбое фазы можно считать, что появился новый осциллятор, а старый исчез, причем амплитуда колебаний не изменилась). Это время t_ст и определяет столкновительную ширину линии Dn_ст:

Dn_ст = 1/2pt_ст (4.18)

Столкновительное уширение однородно, поскольку носит случайный характер и действует в среднем одинаково на все активные частицы одного сорта, участвующие в столкновениях и при этом излучающие. Время t_ст зависит от средней тепловой скорости движения частиц газа u₀ и в каждом конкретном случае требует специального определения. Существенно при этом, что t_ст ~ n_д^-1, где n_д — концентрация частиц газа. Это означает, что Dn_ст ~ р и может достигать заметных величин в диапазоне рабочих давлений. Так, для гелий-неонового лазера крутизна роста столкновительной ширины составляет ~75Мгц/тор, для СО₂-лазера — (4… 8) Мгц/тор. При давлении в единицы и десятки тор, соответствующих рабочим режимам, столкновительная и допплеровская ширины сравнимы, что усложняет расчеты (форма линии не может рассматриваться ни как гауссова, ни как лоренцева). В самом деле, движущиеся частицы излучают не только на частоте, сдвинутой от центра линии в соответствии с эффектом Допплера, но и имеют при этом лоренцево распределение по частотам ввиду конечности времен жизни рабочих уровней. ,В этом случае форм-фактор выражается в виде свертки лоренцева и гауссова профилей, т.е. в виде интеграла

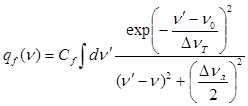(4.19)

Здесь С_f — постоянная, определяемая условием нормировки.

Форм-фактор 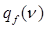называется профилем Фойгта. При заданном соотношении между гауссовой и лоренцевой ширинами линии профиль Фойгта может быть определен путем численного интегрирования. В спектроскопии эти вычисления проведены, и функцию Фойгта можно использовать в виде таблиц и номограмм.

Если ввести параметр S(p) = Dn_ст/Dn_д , отражающий соотношение между столкновительной и доплеровской ширинами, то можно построить для каждого значения S(p) упрощенное выражение для функции Фойгта [2].

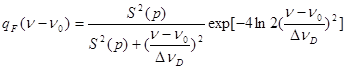(4.20)

Формула (4.20) часто используется в инженерных расчетах.

Роль неоднородного уширения проявляется также в случае лазеров, использующих в качестве активных центров ионы неодима Nd, внедренные в различные твердотельные матрицы [3].

Из кристаллических лазерных сред наибольшее распространение получил алюмо-иттриевый гранат с неодимом (АИГ:Nd). Активными центрами в этой среде являются трехвалентные ионы Nd³⁺ , внедренные в кристаллическую матрицу граната (Y₃Al₅O₁₂). При этом все ионы неодима, попадая в узлы упорядоченной кристаллической решетки, испытывают одинаковое воздействие от своих соседей по решетке. В итоге линия излучения оказывается однородно уширенной с шириной, составляющей при комнатной температуре 6 см^-1 (Dn [см^-1]= (Dn [Гц]/с ).

Те же активные центры, внедренные в стеклянную матрицу, которая не обладает в отличие от кристаллов упорядоченной структурой, оказываются расположенными в различных силовых полях и испытывают в силу этого различные смещения линий излучения. В результате неоднородно уширенная линия излучения стекла, активированного неодимом, имеет ширину, многократно превышающую ширину линии отдельного активного центра, и достигает сотен см^-1. При одинаковой концентрации возбужденных ионов неодима коэффициент усиления в стекле на каждой частоте оказывается примерно во столько же раз меньше усиления в гранате, во сколько раз ширина линии в стекле больше ширины линии в гранате. Эти различия играют решающую роль в реальных лазерах на стекле и гранате, активированных неодимом. Рассмотрим некоторые из них.

1. Благодаря более высокому уровню коэффициента усиления при прочих равных условиях лазеры на гранате имеют меньшие пороги накачки.

2. Существуют режимы работы лазеров «с накоплением инверсной населенности», когда в процессе накачки создаются условия, препятствующие развитию генерации, например, разъюстируют резонатор, нарушая обратную связь. В этом случае процесс накопления инверсной населенности ограничивается процессами снятия возбуждения за счет спонтанных переходов и сверхизлучения (усиленного за счет вынужденных переходов спонтанного излучения). Понятно, что в кристаллической среде эти явления выражены сильнее, чем в стекле, а значит, в кристаллах благодаря высокому усилению при прочих равных условиях может быть накоплена (и потом высвечена в виде короткого импульса) меньшая энергия.

3. На рисунке 4.3 изображены сплошными линиями линии излучения активированного стекла и отдельного иона активатора. При создании инверсной населенности и достижении пороговых условий генерации последняя начнет развиваться в районе максимума линии. В генерации смогут принять только те активные центры, для которых частота генерации находится в пределах их линии излучения. В итоге в инверсной населенности будет «выжигаться дырка», показанная пунктирной линией.

При этом, если уровень накачки достаточен, будет происходить перестройка частоты генерации от первоначального значения («затягивание частоты»), а интегральная ширина спектра излучения окажется много больше, чем в лазере на кристалле с тем же активатором.

Возможность «выжигания дырки» в спектральной линии усиления кристаллов, уширенных неоднородно при низких температурах, была впервые отмечена А. Шавловым [4] в 1961 г.

Аналогичная картина наблюдается и в газовых активных средах с преобладанием доплеровского уширения. Наличие генерации изменяет распределение активных частиц по скоростям, и на доплеровском контуре линии усиления появляется дырка за счет частиц, перешедших в возбужденное состояние. Ширина этой дырки имеет порядок однородной ширины. Впервые этот эффект был обнаружен и детально исследован У. Беннетом в 1962 г [5].

Будучи более экспериментатором, чем теоретиком, Беннет не дал обобщения обнаруженного им эффекта, тогда как построение теоретической модели лазера должно было бы сразу учитывать неоднородный характер уширения. В самом деле, сильная световая волна взаимодействует только с частицами, находящимися в резонансе с полем, и «выжигает дырку» в контуре линии усиления вблизи частоты поля, что и было Беннетом обстоятельно исследовано.

Но внутри резонатора существует стоячая волна, которую можно представить в виде суперпозиции двух навстречу бегущих волн одинаковой частоты. Следовательно, встречная волна должна также выжигать свою дырку, расположенную на контуре линии симметрично относительно первой. По сути дела, лазер черпает энергию из двух групп усиливающих частиц с различными скоростями. При настройке частоты лазера на центр доплеровского контура обе дырки совпадают, и стоячая волна взаимодействует только с одной группой частиц. Это приводит к резонансному падению мощности в центре доплеровской линии усиления. Впервые этот эффект был теоретически рассмотрен У. Лэмбом в своей классической работе «Теория оптических мазеров» [6] и получил название «лэмбовского провала». Лэмбовский провал многократно наблюдался экспериментально и использовался для стабилизации частоты лазера, что способствовало становлению нового направления в науке ― нелинейной лазерной спектроскопии.

Для многих применений лазеров в качестве прецизионного измерительного устройства оказывается важным достичь максимальной монохроматичности лазерного излучения. Это означает, что при неоднородном уширении нелинейные эффекты, приводящие к появлению узких пиков поглощения и усиления, позволяют добиться весьма высоких показателей стабильности частоты выходного излучения лазера, поскольку ширина линии генерации обычно много меньше как ширины линии излучения, так и ширины линии усиления. На ее величину оказывают влияние и режим работы лазера и характеристики резонатора, реальная роль которого гораздо серьезнее, чем просто создание положительной обратной связи.

В развитии нелинейной лазерной спектроскопии главная роль, безусловно, принадлежит советским физикам В.С. Летохову и В.П. Чеботаеву [7]. Углубленное исследование причин, вызывающих нестабильность частоты выходного излучения лазера, и обусловило доминирование радиофизической точки зрения на работу лазера в течение более 30 лет.

Литература к лекции 4

1. Карлов Н.В. Лекции по квантовой электронике. ― М.: Наука, 1983.

2. Люиселл У. Излучение и шумы в квантовой электронике. Пер. с англ. ― М.: Наука, 1972.

3. Микаэлян А.Л., Тер-Микаелян М.Л., Турков Ю.Г. Оптические квантовые генераторы на твердом теле. ― М.: Сов. радио, 1967.

4. Schawlow A.L. Advances in Quantum Electronics. ― N.Y.: Columbia University Press, 1961.

5. Bennett W.R. // Phys. Rew., 1962, 126, 580.

6. Lamb W.E., Jr. // Phys. Rew., 1964, 134, 1429.

7. Летохов В.С., Чеботаев В.П. Принципы нелинейной лазерной спектроскопии. ― М.: Наука, 1975.