Однородное уширение линии излучения.

Любая квантовая система, характеризующаяся дискретным набором энергетических уровней, не может сколь угодно долго находиться в возбужденном состоянии. В этом случая энергия соответствующего состояния может быть определена только с точностью, допускаемой соотношением неопределенностей:

DЕ t ₀ ³ h/2p (4.1),

т.е минимально возможная ширина энергетического уровня

DЕ = h/2pt ₀ (4.2),

где, напомним, h- постоянная Планка; иногда используют величину постоянной Планка ħ=h/2p.

Неопределенность энергии однозначно связана с неопределенностью частоты перехода (рассматриваем пока переходы в основное состояние, время жизни в котором бесконечно велико), то есть линия излучения активного центра при спонтанных переходах будет характеризоваться конечной шириной Dn_л, что ведет к зависимости от частоты вероятности индуцированного перехода в (2.8):

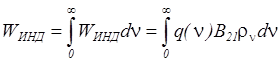(4.3).

Поскольку разница энергий при переходе связана с частотой формулой

Е = hn,

ширина линии излучения рабочего перехода будет равна 1/2pt₀.

Постоянная t₀ является мерой времени, необходимого для того, чтобы система после возбуждения отдала свою энергию. Значение t₀ вообще определяется как вероятностью спонтанного излучения, так и скоростями безызлучательных релаксационных переходов, и может меняться в довольно широких пределах. В отсутствие внешних воздействий (изолированные активные центры) время t_0max определяется исключительно вероятностью спонтанного перехода A₂₁ , поэтому соответствующая ширина линии равна

Dn₀ = A₂₁ /2p (4.4)

и не может быть уменьшена никакими способами. Она называется естественной шириной линии [1].

В реальных условиях активные центры находятся в постоянном взаимодействии с окружающей средой. Это взаимодействие приводит к снижению времени жизни активного центра в возбужденном состоянии, т.е. t₀ << t_реал., при этом ширина линии определяется в основном релаксационными безызлучательными причинами, действующими в направлении установления термодинамического равновесия. Это могут быть столкновения между самими активными частицами (в газовой среде они преобладают), столкновения с частицами другого типа, не участвующими в излучательном процессе, взаимодействия с решеткой кристалла и т.д. Кривая, описывающая зависимость вероятности переходов (а, значит интенсивности излучения) от частоты, называется формой спектральной линии.

Описываемые причины уширения оказывают одинаковое воздействие на все активные центры. Уширение такой природы называют однородным. Можно показать, что форма спектральной линии при однородном уширении описывается функцией Лоренца:

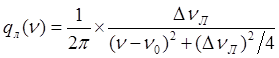(4.5)

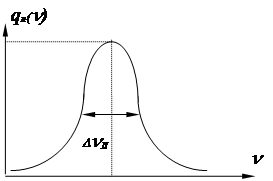
Здесь Dn_Л = 1/2pt₀ — ширина кривой на половине максимальной величины. Максимум лоренцевой функции находится на частоте n₀ (см. рисунок 4.1).

		Рисунок 4.1. Лоренцева форма линии излучения.

В случае, если переход происходит в нижнее состояние, не являющееся основным, то есть обладающее временем жизни t₀₁, то ширина линии Dn_Л будет определяться формулой:

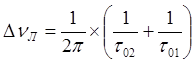(4.6),

учитывающей времена жизни обоих рабочих уровней. Заметим, что выражение (4.5) записано в нормированной форме:

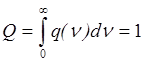(4.7),

поскольку спектрально зависимая вероятность спонтанного перехода при интегрировании должна превращаться в достоверность.

Вероятности спонтанного и вынужденного излучения связаны друг с другом. Поэтому спектральная зависимость усиления повторяет кривую Лоренца, если только все активные частицы равноправно участвуют в актах излучения и поглощения:

W_n^инд = q_л(n)W_инд = q_л(n)B₂₁r_n (4.8)

Рассмотренное уширение спектральной линии, связанное с конечностью времени жизни возбужденного состояния, называется однородным. Такое название дано по следующей причине. Спектральная зависимость q(n) для данного механизма уширения есть единая характеристика как для одной активной частицы, так и для всей совокупности частиц. Наиболее характерные примеры однородного уширения — естественная ширина линии и столкновительное уширение в газах.