Предпроцессорная подготовка

5.1. Основные характеристики конечных элементов

Основные типы КЭ:

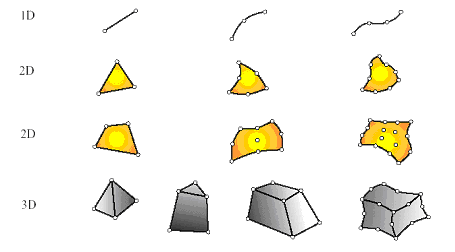
Рис.5.1. Типы КЭ

Конечные элементы могут описываться одной, двумя или тремя пространственными координатами в зависимости от размерности задачи, для решения которой они предназначены. Соответствующее число внутренних или локальных координат называется собственной размерностью элемента. В динамическом анализе время рассматривается как дополнительная размерность.

Каждый элемент описывается множеством характерных точек, называемых узловыми точками или узлами для краткости. Узлы предназначены для описания геометрии элемента и для задания физических степеней свободы (числа неизвестных функций). Узлы обычно находятся в угловых или крайних точках элемента, но могут быть также расположены между угловыми узлами и внутри элемента. Данное различие связано с порядком аппроксимации, который обеспечивает данный конечный элемент. Элементы, имеющие только угловые узлы, называются линейными и обеспечивают линейную интерполяцию геометрии и функций. Элементы, имеющие дополнительные узлы на своих границах между угловыми точками, могут обеспечивать квадратичную или даже кубичную интерполяцию. В первом случае такие элементы называются квадратичными. Отметим также, что существуют элементы, имеющие внутренние узлы. Теоретически такие элементы обеспечивают более точное описание геометрии тела и искомых функций, однако широкого распространения данный тип элементов не получил. При наличии современных автоматических генераторов конечно-элементных сеток часто бывает проще и удобнее разбить конструкцию на большое число линейных элементов простой формы, чем использовать элементы высокого порядка, требующие для построения сетки значительной работы вручную.

Геометрия элемента определяется расположением узловых точек. Большинство элементов, используемых в расчетах, имеют достаточно простую геометрическую форму.

Для конечных элементов, используемых в механических расчетах, определяющее соотношение задает поведение материала, из которого изготовлена конструкция. Например, в качестве такого соотношения во многих случаях используется обобщенный закон Гука, связывающий тензор деформаций и тензор напряжений в точке. Для линейного упругого стержневого элемента достаточно задать один модуль Юнга Е и один коэффициент температурного расширения .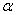

5.2. Типы конечных элементов

При решении задач МКЭ используются элементы различных типов. Наиболее общие из них:

Одномерные элементы: Простейшими среди элементов является одномерный элемент. Схематически он изображается в виде отрезка(рис. 5.2а), хотя и имеет поперечное сечение. Площадь поперечного сечения может изменяться по длине, но во многих встречающихся задачах она считается постоянной. Наиболее часто такой элемент используется в одномерных задачах распространения тепла и в задачах строительной механики при расчете стержневых элементов конструкций.

Простейший одномерный элемент имеет два узла, по одному на каждом конце. Элемент более высокого порядка, трехузловые (квадратичные) и четырехузловые (кубические), изображены на рис. 5.2б и 5.2в. Одномерный элемент может быть криволинейным (рис. 5.2в).

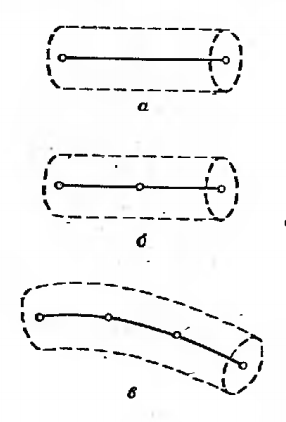
Рис.5.2. Одномерные КЭ

Двумерные элементы: Для построения дискретной модели двумерной области используются два основных семейства элементов: треугольники и четырехугольники. Стороны линейных элементов каждого семейства представляют собой прямые линии (рис 5.3а). Квадратичные и кубические элементы могут иметь как прямолинейные так и криволинейные стороны(рис 5.3б). Возможность моделирования криволинейных границ достигается добавлением узлов в середину сторон элементов. Оба семейства элементов могут быть использованы одновременно внутри области, если только они имеют одинаковое число узлов на стороне(рис 5.3в). Толщина элемента может быть или постоянной, или являться функцией координат.

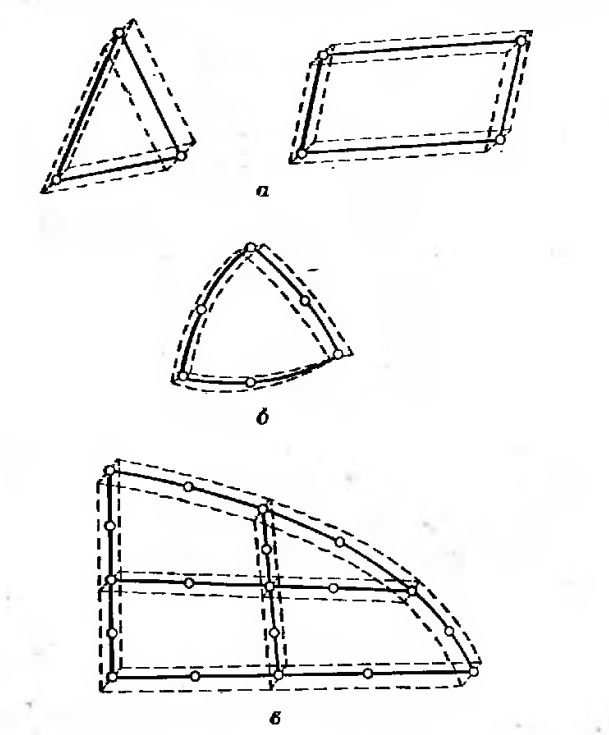
Рис.5.3. Двумерные КЭ

Трехмерные элементы: Наиболее часто встречающимися трехмерными элементами является тетраэдр и параллелепипед (5.4а и б). В обоих случаях линейные элементы ограничены прямолинейными сторонами(плоскостями), тогда как элементы более высокого порядка могут иметь в качестве границ криволинейные поверхности. При разбиении трехмерного тела трудно наглядно представить расположение элементов в дискретной модели, поэтому, вероятно, более желательным из этих двух типов является параллелепипед.

На рис 5.4в показан другой вид элементов, которые используются при рассмотрении тел цилиндрической формы. Эти элементы подобны двумерному треугольнику и позволяют еще учесть изменение неизвестной величины вдоль третей координаты.

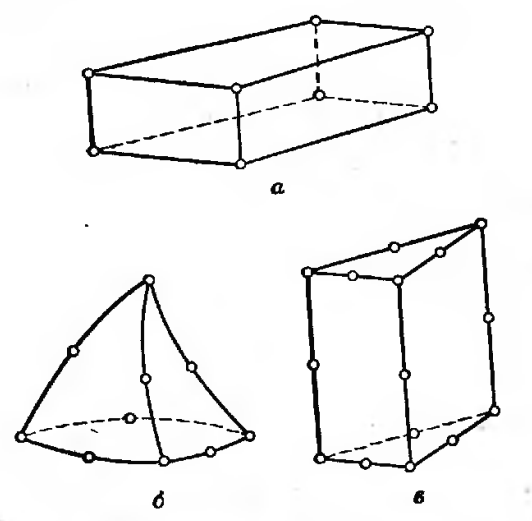
Рис.5.4. Трехмерные КЭ

На рис 5.5 показан элемент широко используемый в осесиметрических задачах. Этот элемент образуется поворотом треугольника на 360º. Подобный элемент может быть получен вращением четырехугольника.

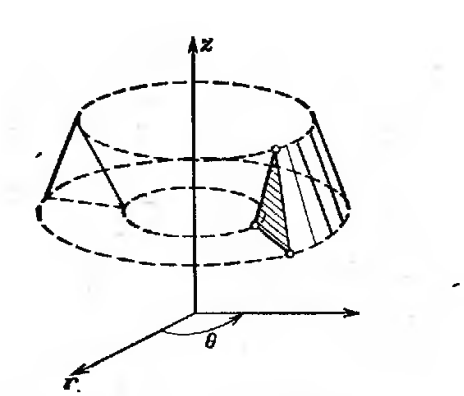
Рис.5.4. Осесимметричный КЭ