Введение в метод конечных элементов

В реальных конструкциях почти всегда присутствуют сложные формы, состоящие к тому же из различных материалов. Метод конечных элементов является наиболее популярным численным методом решения задач проектирования конструкций сложных форм.

Дискретизация.

Анализ методом конечных элементов начинается с дискретизации исследуемой области (области задачи) и делении ее на ячейки сетки. Такие ячейки называют конечными элементами.

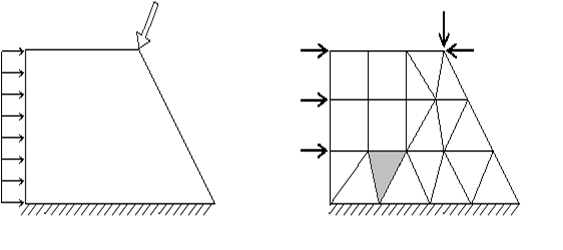
Конечные элементы могут иметь различную форму. В отличие от реального сооружения в дискретной модели конечные элементы связываются между собой только в отдельных точках (узлах) определенным конечным числом узловых параметров.

Выбор подходящих элементов с нужным количеством узлов из библиотеки доступных элементов является одним из наиболее важных решений, которые приходится принимать пользователю пакета конечноэлементного анализа. Конструктору так же приходится задавать полное количество элементов (другими словами, их размер).

Основная проблема МКЭ – построение сетки, особенно для объекта сложной геометрии. Создание трехмерных сеток конечных элементов обычно представляет собой трудоемкий и кропотливый процесс.

Классическая форма метода конечных элементов называется h-версия. В качестве функции формы в данном методе применяются кусочные полиномы фиксированных степеней, а повышение точности достигается уменьшением размера ячейки. В p-версии используется фиксированная сетка, а точность повышается благодаря увеличению степени функции формы. Общее правило состоит в том, что чем больше количество узлов и элементов (в h-версии) или чем выше степень функции формы (p-версия), тем точнее оказывается решение, но тем дороже оно стоит с вычислительной точки зрения. Одной из САПР, в которой реализована p-версия МКЭ, является Pro/Engineer(CREO).

Ансамблирование:

Ансамблирование или сборка представляет собой объединение отдельных элементов в конечно-элементную сетку. С математической точки зрения ансамблирование состоит в объединении матриц жесткости отдельных элементов в одну глобальную матрицу жесткости всей конструкции. При этом существенно используются две системы нумерации узлов элементов: локальная и глобальная. Локальная нумерация представляет собой фиксированную нумерацию узлов для каждого типа конечных элементов в соответствии с введенной локальной системой координат на элементе. Глобальная нумерация узлов всей конструкции может быть совершенно произвольной, также как и глобальная нумерация конечных элементов. Однако, между локальными номерами и глобальными номерами узлов существует взаимнооднозначное соответствие, на основе которого и формируется глобальная система конечно-элементных уравнений.

Аппроксимация

МКЭ относится к методам дискретного анализа. Однако в отличие от численных методов, основывающихся на математической дискретизации дифференциальных уравнений, МКЭ базируется на физической дискретизации рассматриваемого объекта. Реальная конструкция как сплошная среда с бесконечно многим числом степеней свободы заменяется дискретной моделью связанных между собой элементов с конечным числом степеней свободы. Так как число возможных дискретных моделей для континуальной области неограниченно велико, то основная задача заключается в том, чтобы выбрать такую модель, которая лучше всего аппроксимирует данную область.

Сущность аппроксимации сплошной среды по МКЭ состоит в следующем:

1. рассматриваемая область разбивается на определенное число КЭ, семейство элементов по всей области называется системой или сеткой конечных элементов;

2. предполагается, что КЭ соединяются между собой в конечном числе точек – узлов, расположенных по контуру каждого из элементов;

3. Для каждого КЭ задается аппроксимирующий полином.

Аппроксимирующие функции :

Аппроксимирующий полином для одномерного КЭ: u(x)=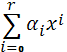

Пример для одномерного КЭ:

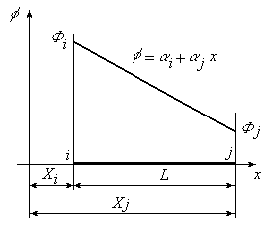
Пример для двумерного КЭ:

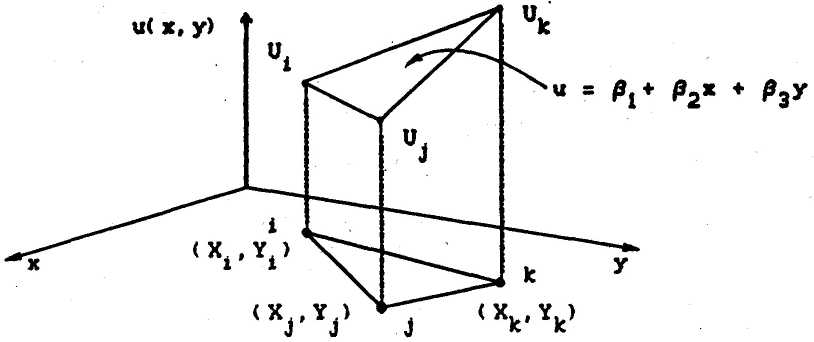
Аппроксимирующий полином второго порядка: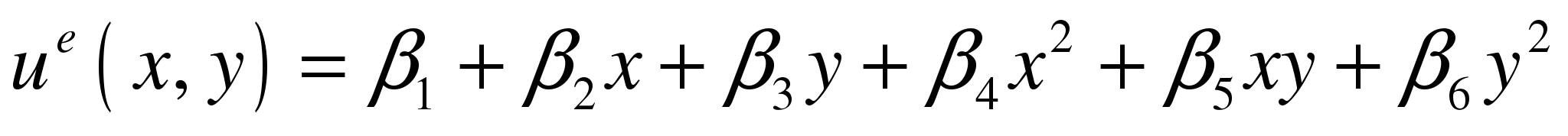

Степень аппроксимирующего полинома определяет число узлов, которым должен обладать элемент, – оно должно равняться числу неизвестных коэффициентов 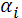, входящих в полином.

Искомые функции в пределах каждого КЭ (например, распределение перемещений, деформаций, напряжений и т. д.) с помощью аппроксимирующих функций выражаются через узловые значения, представляющие собой основные неизвестные МКЭ.

Искомая аппроксимирующая функция:

u( )=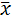

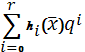
h(x)-координатные/базисные функции, т.н. функция формы;

q - неизвестные коэффициенты(значения в узлах).

В матричном виде:

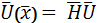
Аппроксимация, как правило, дает приближенное, а не точное, описание действительного распределения искомых величин в элементе. Поэтому результаты расчета конструкции в общем случае также являются приближенными. Закономерно может быть поставлен вопрос о точности, устойчивости и сходимости решений, полученных МКЭ.

Под точностью понимается отклонение приближенного решения от точного или истинного решения. Устойчивость, прежде всего, определяется ростом ошибок при выполнении отдельных вычислительных операций. Неустойчивое решение является результатом неудачного выбора аппроксимирующих функций, «плохой» разбивки области на КЭ, некорректного представления граничных условий и т. п. Под сходимостью подразумевается постепенное приближение последовательных решений к предельному, по мере того как уточняются параметры дискретной модели, такие как размеры элементов, степень аппроксимирующих функций и т. п. В этом смысле понятие сходимости аналогично тому значению, которое оно имеет в обычных итерационных процессах. Таким образом, в сходящейся процедуре различие между последующими решениями уменьшается, стремясь в пределе к нулю.

Перечисленные выше понятия иллюстрируются рис. 3.1. Здесь абсцисса обозначает степень уточнения параметров дискретной модели, а ордината определяет полученное при этом уточнении приближенное решение. На графике показан монотонный тип сходимости, при котором точность решения повышается плавно.

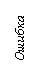
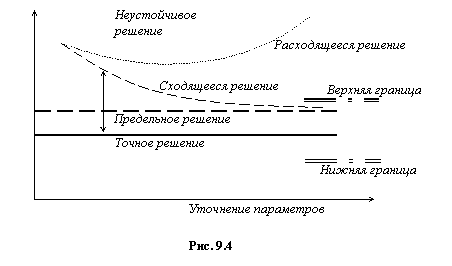
Рис.3.1. Зависимость решения от параметров