детерминированных конечных автоматов и А-грамматик

Недетерминированный автомат (НДА) - это автомат, где значение функции переходов d - не отдельное состояние, как в детерминированном автомате (ДА), а множество состояний. В общем случае уНДА может быть также не одно, а множество начальных состояний (если начальное состояние не единственно, то эти состояния при изображении таблицы переходов будут помечаться стрелкой).

НДА изучается, так как для заданного множества иногда легче найти недетерминированное описание.

Говорят, что НДАдопускает входную цепочку, если он позволяет связать одно из его начальных состояний с одним из допускающих.

Так автомат, представленный на рис. 3.2, допускает цепочку 11, так как

,

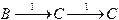причем В - начальное, а С - допускающее состояния. Существование одной этой последовательности достаточно, чтобы показать допустимость входной цепочки 11, и существование другой последовательности

,

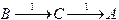где A - отвергающее, на это не влияет.

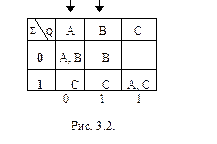
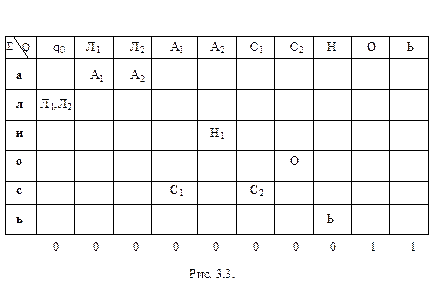
На рис. 3.3 представлен еще один НДА с входным алфавитом {а, л, н, о, с, ь}, который допускает только две цепочки лассо и лань.

Понятие НДА приобретает практическое значение, так как для каждого НДА существует эквивалентный ему ДА, то есть ДА, допускающий в точности те же цепочки, что и НДА.