Анализ конечных автоматов
Полное описание поведения автомата заключается в определении последовательности выходных сигналов при возбуждении его в тактовые моменты времени некоторой последовательностью входных сигналов. Входная и выходная последовательности представляются наборами символов (или их номеров) из алфавитов X и Y одинаковой длины l. Для такого описания, кроме характеристических функций, необходимо определить или задать начальное состояние автомата.
Наиболее удобно определять реакцию автомата на входную последовательность по его графу. Для этого достаточно проследить путь в графе, начиная от вершины начального состояния, по направлению дуг, которые отмечены очередными номерами из входной последовательности. Выходная последовательность определяется номерами, которыми отмечены дуги в порядке их следования по пройденному пути, а последовательность состояний автомата – номерами вершин, через которые проходит этот путь.
Так, из графа на рис. 2 для входной последовательности (2, 0, 1, 1, 2, 3) и начального состояния 0 имеем выходную последовательность (0, 1, 0, 0, 1, 1) и смену состояний автомата (1, 3, 0, 2, 2, 3). При начальном состоянии 2 и той же входной последовательиости получаем соответственно (1, 1, 0, 0, 1, 1) и (2, 3, 0, 2, 2, 3).
С помощью графа автомата легко выделить следующие характерные типы его состояний:
1) преходящее состояние, из которого можно перейти, по крайней мере, в одно другое состояние, но после этого уже нельзя возвратиться в него ни при каком воздействии (соответствующая вершина не имеет заходящих дуг, но имеет хотя бы одну исходящую дугу);
2) тупиковое состояние, в которое можно перейти, по крайней мере, из одного другого состояния, но после этого уже нельзя выйти из него ни при каком воздействии (соответствующая вершина не имеет исходящих дуг в другие вершины, но имеет хотя бы одну входящую дугу из другой вершины);
3) изолированное состояиие, из которого нельзя перейти ни в какое другое состояние и в него нельзя попасть ни из какого другого состояния (соответствующая вершина содержит только петлю).
Аналогичиые определения можно дать для некоторых совокупностей состояний, рассматриваемых как подавтоматы. Если начальное состояние автомата М принадлежит непустому множеству Si состояний, которое составляет тупиковый или изолированный подавтомат, то М можно упростить исключением всех состояний, которые не принадлежат множеству Si, и всех дуг, начинающихся в этих состояниях.
 | |||||
 | |||||
| |||||
Рис. 3
Пусть М1, М2, и М3 – соответственно преходящий, тупиковый и изолированные подавтоматы автомата М, которые характеризуются множествами состояний S1, S2, и S3. Очевидно, выделение таких подавтоматов соответствует разбиению множества S состояний автомата М на непересекающиеся подмножества S1, S2, и S3, представляющие собой классы эквивалентности (S1 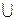 S2
S2 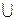 S3= S и S1
S3= S и S1 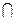 S2
S2 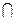 S3=
S3= 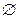 ).Как следует из обобщенного графа (рис.3), матрица соединения автомата может быть представлена в виде:
).Как следует из обобщенного графа (рис.3), матрица соединения автомата может быть представлена в виде:
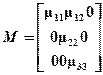 ,
,
где m11, m22, m33 – матрицы подавтоматов М1, М2, и М3; m12 - матрица, характеризующая переходы от состояний преходящего автомата М1 к состояниям тупикового автомата М2. Отсюда следует, что разбиение автомата М на подавтоматы М1, М2, и М3 можно осуществить преобразованием его матрицы соединений к стандартному виду путем перестановки соответствующих строк и столбцов.
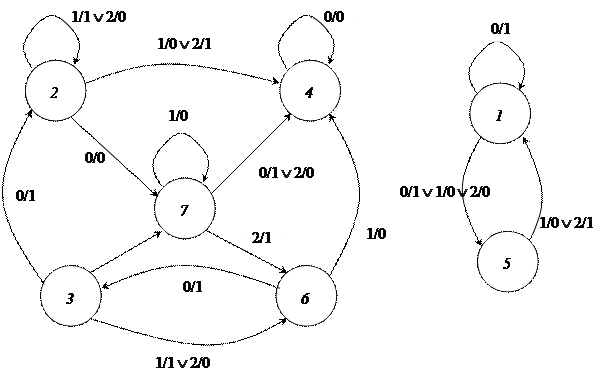 |
Рис. 4
Например, для автомата, граф которого изображен на рис. 4, имеем:
| 2/0 | 0/1 | 1/1 | ||||||
| 1/0 | 1/0 | 2/1 | ||||||
| M = | 1/1 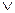 2/0 2/0
| 0/0 | ||||||
1/0 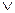 2/1 2/1
| 0/0 | |||||||
0/1 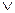 2/0 2/0
| 1/0 | |||||||
| 0/1 | 1/0 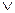 2/1 2/1
| |||||||
0/1 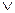 1/0 1/0  2/0 2/0
|
Дата добавления: 2020-06-09; просмотров: 760;











