Основные параметры ЦАП

Из всего перечня статических и динамических параметров, характерных для интегральных устройств, остановимся на основных параметрах ЦАП, характеризующих их функциональные показатели.

Число разрядов – определяет максимальное количество кодовых комбинаций на входе ЦАП в двоичном коде – 2 ⁿ. Каждое значение входного кода преобразуется в дискретное значение выходной аналоговой величины. Дискретность изменения выходной аналоговой величины зависит от числа разрядов ЦАП. Отклонение конкретного значения выходной аналоговой величины от номинального определяется точностью изготовления устройств и элементов интегрального исполнения, входящих в ЦАП, и не зависит от числа разрядов. Совокупность значений аналоговой выходной величины в функции значений цифрового кода называется характеристикой преобразования. При последовательном возрастании цифрового кода через единицу младшего разряда (ЕМР) выходной сигнал образует ступенчатую функцию. На рис. 4.7 приведена номинальная характеристика преобразования 4-разрядного ЦАП с однополярным выходным сигналом U _вых(t). При отсутствии аппаратных погрешностей характеристика преобразования представляет ломаную линию 1, вершины ступенек которой лежат на идеальной характеристике преобразования 2. На характеристике можно отметить определенные точки.

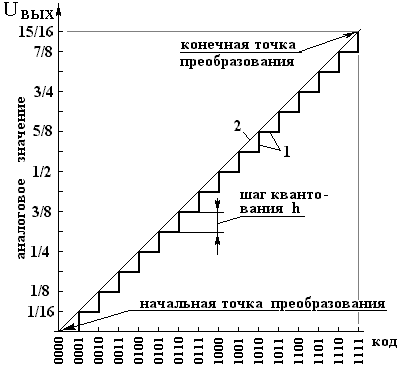
Рис. 4.7

Прежде всего это начальная и конечная точки преобразования, которые определяются начальным и конечным значениями кода. Начальной точкой является точка начала координат, соответствующая нулевому значению выходной величины при значении кода, равном нулю (в нашем примере коду 0000). Конечная точка определяется максимальным значением выходной аналоговой величины, соответствующей максимальному значению цифрового кода (в нашем случае максимальный код 1111, а значение выходной величины составляет 15/16 частей полной шкалы). Интервал значений аналоговой выходной величины от начальной до конечной точки называют диапазоном выходной величины.

Разность между максимальным и минимальным значениями аналоговой выходной величины называют ее амплитудой.

Разрешающая способность определяется приращением аналоговой выходной величины, соответствующим изменению цифрового кода на единицу младшего разряда (1МР или ЕМР). Это приращение называется шагом квантования – h. Для двоичного линейного ЦАП все шаги квантования одинаковы и равны:

h = (U_{вых max} – U_{вых min})/(2 ⁿ – 1) = U _m/(2 ⁿ – 1), (4.7)

где U _m – амплитуда выходной величины или величина опорного напряжения U _оп; n – разрядность ЦАП.

Очевидно, что, чем выше разрядность преобразователя, тем выше его разрешающая способность. Разрешающая способность может выражаться в процентах от полной шкалы аналогового сигнала.

Абсолютная погрешность преобразования δ_пш – отклонение выходного сигнала от расчетного в конечной точке характеристики преобразования. Абсолютная погрешность чаще всего выражается в долях младшего разряда, а её типичная величина не должна превышать ± 0,5 ЕМР.

Нелинейность δ_л характеристики преобразования – максимальное отклонение реальной характеристики от теоретической (прямой линии, соединяющей точку нуля и максимума выходного сигнала). Определяется в долях ЕМР.

Время установления t _уст – является динамическим параметром ЦАП и оценивается интервалом времени, за который от момента поступления кода до момента, когда выходной сигнал достигает установившегося значения с заданной погрешностью (обычно ± 0,5 ЕМР).

Этот параметр определяет быстродействие ЦАП. Если t_уст £ 100 нс, то ЦАП считаются быстродействующими.

4.3. Основные понятия и параметры
аналого-цифровых преобразователей

Цифровые вычислительные машины (ЦВМ), используемые в системах обработки информации и управления, могут оперировать только с дискретными величинами. Поэтому непрерывные величины для их обработки цифровой вычислительной машиной должны быть преобразованы в дискретные, что достигается с помощью специальных устройств, получивших название аналогово-цифровых преобразователей (АЦП). В АЦП входным сигналом является напряжение, а выходным – соответствующий его уровню цифровой код. Процесс дискретизации заключается в квантовании непрерывного входного сигнала как по времени, так и по уровню (рис. 4.8).

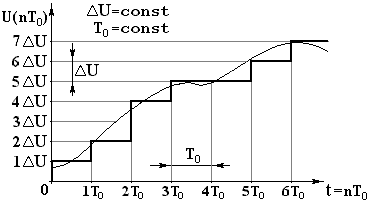
Рис. 4.8

Полномасштабный диапазон изменения непрерывной величины разбивается на ряд, как правило, одинаковых дискретных значений времени Т₀ и ряд значений равноотстоящих на ΔU уровней. Расстояние между двумя соседними значениями дискретных величин называется шагом квантования. Так как квантование по времени ведется с фиксированной периодичностью, то этот шаг называют периодом квантования Т₀. Преобразование непрерывного сигнала происходит путем выполнения ряда операций. Во-первых, в дискретные моменты времени nT₀ (n = 0,1,2, …) делается выборка значения непрерывной функции U(t) и это значение фиксируется. На следующем шаге это фиксированное значение сопоставляется с одним из ближайших уровней дискретной функции U(nT₀). Например, для момента времени 3Т₀ значение непрерывной функции U(t) ближе к уровню 5ΔU. Именно этот уровень затем кодируется. При другом значении t = 5Т₀ значение непрерывной функции ближе к уровню 6ΔU, которому соответствует другое значение цифрового кода. Таким образом, каждому дискретному значению функции ставится в соответствие свой цифровой код.

Параметры АЦП

Одним из значимых параметров АЦП является их разрядность – n, определяемая целочисленной величиной n = log₂N, где N – число значений выходного цифрового кода.

При подаче на вход АЦП линейно возрастающего напряжения на выходе идеального преобразователя наблюдается последовательное изменение цифрового кода (соответствующего ему дискретного значения напряжения U_αi). Зависимость выходного цифрового кода от значений входного аналогового напряжения U_вх называется характеристикой преобразованияАЦП (рис. 4.9).

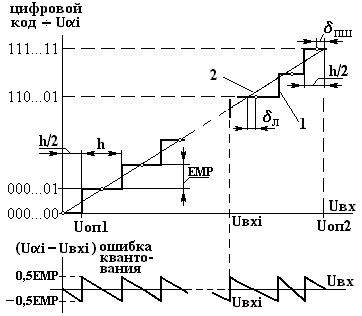
Рис. 4.9

Изменение входного напряжения, соответствующее ЕМР (изменению кода на единицу), называют напряжением межкодового перехода. Напряжение межкодового перехода, при котором значение кода остается постоянным, определяет шаг квантования h. Чтобы начальное значение U_вх = 0 соответствовало коду 000…00 (идеальная прямая 2 проходит через начало координат), характеристика преобразования должна отстоять от оси ординат на полшага (h/2) квантования (ступенчатая линия 1). При преобразовании аналоговой величины в цифровой код с конечным числом разрядов возникает систематическая ошибка, которая называется ошибкой квантования. В нижней части рис. 4.9 представлен график ошибки квантования, из которого очевидно, что она составляет ± 0,5 ЕМР, то есть имеет величину, равную половине ступеньки дискретного напряжения при изменении кода на единицу младшего разряда.

Нелинейность АЦП – δ_л (δ_L)отклонение действительного значения входного напряжения, соответствующего заданной точке характеристики преобразования, от значения, определяемого по линеаризованной характеристике в той же точке. Этот параметр определяет отклонение центров ступенек действительной характеристики преобразования 1 от прямой линии 2, аппроксимирующей номинальную характеристику.

Абсолютная погрешность δ_пшв конечной точке шкалы – это разность между теоретическим и фактическим аналоговыми значениями входного напряжения в конечной точке характеристики преобразования. Абсолютная погрешность учитывает погрешности коэффициента передачи, смещения нуля, нелинейность и шум. Измерения абсолютной погрешности должны проводиться в стандартных условиях с применением источников питания и измерительных приборов, отвечающих международным стандартам.

Быстродействие АЦП характеризуется рядом динамических параметров, среди которых можно выделить время преобразования t_прб, частоту преобразования.

Время преобразования определяется отрезком времени от начала изменения сигнала на входе АЦП (аналогового или цифрового) до появления на выходе соответствующего устойчивого кода.

Частота преобразованиязависит от частоты преобразуемого аналогового сигнала и, согласно теореме В.А. Котельникова, должна, по меньшей мере, вдвое превышать максимальную частоту преоб­разуемого сигнала.